L'optimisation combinatoire occupe une place trés
importante en Recherche Operationnelle, en mathématiques
discrètes et en informatique. Son importance se justifie d'une part par
la grande difficulté des problémes d'optimisation et d'autre part
par de nombreuses application pratiques pouvant être formulées
sous la forme d'un probléme d'optimisation combinatoire. Bien que les
problèmes d'optimisation combinatoire soient souvent faciles à
définir, ils sont généralement difficiles à
résoudre. En effet, la plupart de ces problèmes appartiennent
à la classe des problémes NP-difficiles et ne possédent
donc pas à ce jour de solution algorithmique efficace valable pour
toutes les données.
Pour la résolution des problèmes, en recherche
opérationnelle, le choix de la méthode de résolution
constitue une étape cruciale. Il existe deux grandes familles de
méthodes de résolution. D'un coté, les méthodes
exactes (complétes) qui garantissent la complétude de la
résolution, de l'autre les méthodes approchées
heuristiques métaheuristiques (incomplétes) qui perdent en
complétude pour gagner en efficacité.
La principale différence entre ces deux familles
réside dans le fait que la qualité des résultats
donnés par les heuristiques n'est pas garantie par la théorie.
Les méthodes exactes soutenues par la théorie, aboutissent aux
solutions optimales du problème. En pratique, les méthodes
exactes sont sensiblement liées à la taille du problème et
leur utilisation est sanctionnée par des temps d'exécution
souvent inacceptables. Tandis que les heuristiques et métaheuristiques
montrent qu'elles peuvent aboutir à des résultats très
satisfaisants en des temps beaucoup plus raisonnables.
Le seul moyen connu pour déterminer le nombre
chromatique d'un graphe G est de faire une énumération
(implicite) de toutes les colorations de G. On commence en
général par considérer une borne supèrieure q de
XG.
Une méthode standard d'une telle
énumération consiste à considérer un ordre de
sommets V1, ,Vn. Soit q la plus petite valeure pour laquelle il
existe une q - coloration lors du processus d'énumération.
Comme nous savons que le nombre chromatique XG est inferieur
ou égale a N (nombre max de couleur), nous posons initialement q est
égale a N, puis nous colorons successivement les sommets V1, ,V
n avec la plus petite couleure possible. Si une couleur inferieure
à q est affectée à chaque sommet, alors une coloration en
q1 < q couleurs à été obtenue.
Nous posons q = q1, et nous effectuons marche arrière
jusqu'au sommet Vj tel que Vj+1 soit le premier sommet coloré avec la
couleur q1. Nous tentons d'attribuer à Vj la plus petite couleur
possible, supérieure à la couleur courante et inferieure à
q. Si une telle couleur est trouvée, alors nous procédons comme
auparavant en colorant itérativement les sommets Vj+1
à Vn.
Si à une certaine étape, la plus petite couleur
pour un certain sommet V, est égale a q, alors nous effectuons une
marche arrière jusqu'au sommet Vp_1 et nous poursuivons le
processus comme précédemment.
L'algorithme se termine lorsque nous devons faire marche
arrière à partir du sommet V1.
[// {On a: w(G) XG max dG , pour notre cas, la taille de la
clique max est égale à trois d'ou: w(G) = 3,et le deg max du
graphe est égale à: 6, donc on en déduit que: 3 XG
6.//}.
Cette méthode peut se résumé comme suit
:
Etapel:
L'étape une est basée sur l'algorithme
séquentiel suivant:
· Poser q égale au nombre maximum de couleur N.
· Pour chaque sommet d'un graphe G, déterminer les
degrés, puis classer les sommets dans l'ordre décroissant de
leurs degrés.
· Parcourir la liste des sommets du graphe (i := 1 a n)
, en attribuant à chaque sommet xi la plus petite couleur possible,
c'est-à-dire la plus petite couleur qui n'est pas utilisée par x
adjacent à xi, pour tout j <i.
· Si la couleur q n'a pas été
utilisée, nous avons obtenu une coloration en q1 <q couleurs, et
remplaçons q par q1(q := q1).
Etape 2:
· Faire marche arrière (en décolorant les
sommets) jusqu'au sommet xr tel que xr+1 ait
été le premier sommet à avoir la couleur q.
· Nous recolorons xr avec la plus petite couleur
possible qui soit plus grande que sa couleur courante.
· Recolorier à nouveau les sommets xr, .
. . , x avec l'algorithme séquentiel.
· Si à un moment donné la couleur q doit
être affectée à un sommet x5 (ce que nous
voulons éviter, puisque nous voudrions utiliser moins de q couleurs),
nous remontons dans l'algorithme séquentiel jusqu'au sommet
x5_1 et faisons comme précédemment (c'est-à-
dire recolorer x5_1 avec la plus petite couleur possible qui soit
plus grande que sa couleur courante et continuer).
· L'algorithme se termine lorsque l'on est remonté
jusqu'à x1, et XG est égal à la valeur courante de q.
Exemple illustratif
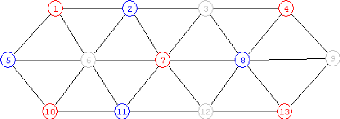
Figure 4.1 :Exemple illustratif



