La technique Tabou est une méthode
générale d'optimisation combinatoire qui a été
introduite par Glover dans un cadre particulier et développée
plus tard dans un contexte plus générale. Indépendament,
Hansen a developpé la méthode de SAMD (del'anglais Steepest
Ascent Mildest Descent) qui se base sur des idées similaires. La
technique Tabou s'est déja montrée trés performante pour
un nombre considérable de probléme d'optimisation
combinatoire.
En ce qui concerne notre cas, nous donnerons tout d'abord une
description générale de la méthode Tabou, puis nous
présenterons l'adaptation de cette technique au probléme de la
coloration baptisé TABUCOL par M Dominique de Werra (Werra,1993).
La technique Tabou
Le probléme d'optimisation combinatoire qui nous
intéresse est le suivant : étant un ensemble X de solutions
admissibles et une fonction f définie sur X, il s'agit de
déterminer une solution s* 2 X minimisant f sur X.
Definissons un voisinage N(s) pour toute solution s 2 X; Nous
utiliserons une technique qui consiste à se déplacer de solution
s en solution voisine s' 2 N(s) ,tout en essayant de minimiser la
fonction f.
De nombreuses heuristiques ont été
développées dans ce même contexte; la plus connue
étant certainement la méthode de descante: tant qu'il existe une
solution s'voisine de la solution courante s et telle que
f(s') < f(s). ,on se déplace de s vers s' qui
devient ainsi la nouvelle solution courante. Cette méthode de descente
s'arrête donc au premier minimum local rencontré. Le principal
inconvénient de cette technique provient alors du fait que la valeur de
cet optimum local peut être largement supérieur à celle
d'un optimum globale.
Pour cette raison, de nombreuse heuristiques ont
été étudiées afin d'éviter le piége
que représentent ces minima locaux. Ainsi, par exemple, la methode du
R~ecuit Simul~e est conçue de telle maniére
qu'il est relativement aisé de sortir d'un optimum locale tant que la
température (un paramétre) est assez élevée. Cette
température dimine lentement au cours de l'algorithme et lorsqu'elle
atteint une valeur assez basse. On se trouve finalement bloqué dans un
optimum qu'on espére globale mais qui sera probablement bien meilleur
que le premier optimum local rencontré.
Une telle méthode présente un certain nombre
d'inconvéniants dont le plus important découle de la manipulation
délicate du paramètre qu'est la température : Il est non
seulement difficile de donner une valeur initiale à cette
température, mais de plus sa décroissance doit être
réglée de maniére à donner assez de temps à
l'algorithme pour atteindre un optimum globale sans lui en faire perdre trop
à des températures élevées car on risque alors de
visiter un trop grand nombre de solutions largement moins bonnes que cet
optimum global.
Une toute autre méthode générale
d'optimisation combinatoire a été proposée par Glover: il
s'agit de la technique Tabou que nous noterons TS (de l'anglais Tabu Search).
L'une des idées principales constituant cette méthode consiste
à choisir à chaque déplacement la meilleure solution
voisine s' de la solution courante s.
Tant que l'on ne se trouve pas dans un optimum local, TS se
comporte donc comme la méthode de descente et améliore à
chaque étape la valeur de la fonction objectif. Lorsque l'on atteint pa
r contre un optimum, TS choisit le moins mauvais des voisins, c'est-a-dire
celui qui donne un accroissement aussi faible que possible à la fonction
objectif.
L'inconvénient que présenterait une
méthode basée sur cet unique principe serait que si un minimum
local s se trouve au fond d'une vallée profonde, il serait impossible de
ressortir de celle-ci en une seule itération, et un déplacement
de la solution s vers une solution s' 2 N'(s) avec
f(s') > f(s) pourrait provoquer, à l'itération
suivante, le déplacement inverse puisque s 2 N(s') et
f(s') <f(s); on risquerait donc de cycler autour de ce minimum
local.
C'est pour cette raison que TS s'appuie sur un
deuxiéme principe qui consiste à garder en mémoire les
dernières solutions visitées et à interdire un retour vers
celles-ci pour un nombre fixé d'itérations. Le but étant
de donner assez de temps à l'algorithme pour lui permettre de sortir de
toute vallée contenant un minimum local. En d'autres termes, TS conserve
à chaque étape une liste T de solutions "taboues", vers
lesquelles il est interdit de se déplacer momentanément.
'
Lors du choix de la meilleure solution sE N(s), il est
possible que l'on ait à départager plusieurs candidats donnant
certes, une même valeur à la fonction objectif, mais ne nous
dirigeons pas tous vers un optimum global. Il est ainsi parfois souhaitable de
pouvoir retrourner
vers une solution visitée s, malgré le fait
qu'elle fasse parite de la liste T des solutions taboues, ceci afin d'explorer
une nouvelle région voisine de s.
Pour cette raison , TS fait intervenir un nouvel
ingrédient appelé fonction d'aspiration et définie sur
toutes les valeurs de la fonction objectif: lorsqu'une solution s'
voisine de la solution s fait parite de T et satisfait de plus notre aspiration
{c'est-à-dire f(s') A(f(s))} ,on lève le
'
statut tabou de cette solution set elle devient donc candidate
lors de la sélection du meilleur voisin de s.
Il nous faut encore définir une condition d'arrêt.
On se donne en général un nombre maximum d'itérations
entre deux améliorations de la meilleure solution s*
rencontrée.
Dans certains cas, il est possible de déterminer une
borne inférieure f* de la fonction objectif et on peut alors
stopper la recherche lorsqu'on a atteint une solution s de valeur f(s) proche
de f*.
L'algorithme Tabou peut être décrit par
l'algorithme suivant :
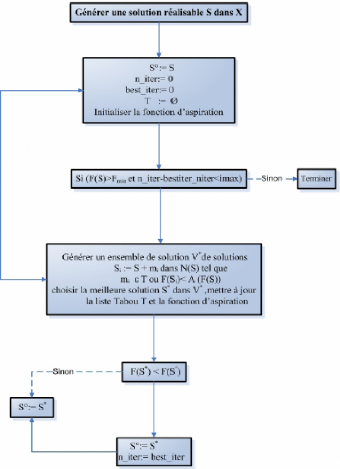
Organigramme de la méthode de recherche tabou
Tabou adaptée à la coloration de graphe
Nous allons adapter TS à la déremination d'une
k - col oration dans un graphe G pour un nombre de couleurs k fixé.
L'algorithme ainsi obtenu sera l'ingrédient principal de la méta-
heuristique suivante :
k := borne superieure du nombre chromatique XG d'un graphe G;
tant que TABUCOL est capable de déterminer une (k -- 1)--coloration dans
G faire
k := k -- 1;
On peut représenter une coloration d'un graphe comme
une partition de ses sommets en ensembles stables. l'objectif de TABUCOL
consiste donc à construire une partition des sommets d'un graphe G = (V,
E) en un ensemble k fixé d'ensembles indépendants. Nous avons
défini l'espace X des solutions comme étant l'ensemble des
partition (V1 , ...., Vn) de V en k sous ensembles non forcément
stables.
La fonction objectif f comptabilise le nombre d'arêtes
ayant leurs deux extrémités dans une même partie Vi. En
d'autres termes f = Eki= 11E(Vi)1 .et cherchons à la
minimiser.
Ainsi f(s = (V 1, ....., Vn)) = 0 ssi S est une k --
coloration de G. Nous pouvons donc fixé f = 0 et arrêter la
recherche si l'on visite une solution s telle que f (s) = 0.
Une soloution s' = (V,1 ,
..., V,n) est considérée comme voisine
d'une solution s = (V1, ....., Vn) si on peut l'obtenir à partir de s en
ne déplaçant qu'un seul sommet x d'un sous ensemble Vi à
un sous ensemble Vj .Ainsi :
Vi, = Vi / {x} ; Vi, = Vi U {x} ;
Vr, = Vr pour tout r = 1......k r =6 i, j;
Il serait peu réaliste de considérer une liste
T de solutions taboues. En effet, elle demanderait trop de place en
mémoire et nous perdrions trop de temps à tester si une solution
de V# fait parite de T. Nous avons donc décidé de ne
mémoriser qu'une information moins complète. Lorsqu'un sommet x
se déplace d'un ensemble Vi à un ensemble Vj, le
couple (x, i) devient tabou, ce qui signifie que le sommet x n'est pas
autorisé à revenir dans l'ensemble Vi pour un nombre 1T1
d'itérations. La taille 1T1 = 7 s'est expérimentalement
avérée satisfaisante.
Il est parfois souhaitable de lever un tel statut tabou,
surtout lorsque le retour de x dans Vi donne une solution s n'ayant encore
jamais été visitée et de petite valeur f(s). Nous avons
définit la fonction d'aspiration comme étant égale
à la valeur f (s*) de la meilleure solution s*
rencontrée. Considérons donc une solution s, de
V* obtenue à partir de la solution courante s en
déplaçant un sommet x dans une partie Vi, et suposons que (x, i)
E T; si f (s,) < f (s*), Nous levons le statut tabou
de s' qui devient ainsi candidat pour le choix de la meilleure
solution dans V*.
Le principal critère d'arrêt de la
méthode Tabou est la découverte d'une solution s avec f (s) = 0,
c'est-à-dire d'une k -- coloration. On peut alors diminuer la valeur de
k d'une unité et appliquer à nouveau la méthode Tabou,
afin de tenter d'obtenir une meilleure borne supérieure sur le nombre
chromatique. Mais ce critère d'arrêt ne permet pas d'assurer que
l'algorithme s'arrête; en particulier si k < XG, il n'est pas
suffisant. Il faut donc introduire un ou plusieurs autres critères
d'arrêt pour interrompre la recherche. Les plus fréquents sont
:
· un nombre fixé d'itérations à
été effectué.
· il n'y a plus eu d'amélioration de s*
depuis un nombre fixé d'itérations.
· le temps de calcul a atteint une limite fixée.
Nous obtenons ainsi la méthode Tabou pour le
problème de la k - coloration décrit ci- dessous. Notons qu'afin
d'accélerer un peu l'aglorithme, la génération de M
peut



