3.5.1 Modélisation mathématique
Les données du problème
N : nombre de stations.
NF: nombre de fréquences disponibles.
C [j]: nombre de cellules à considérer.
R[j]: pour chaque station i, nous connaissons le nombre de
fréquence requis.
Contrainte:
- Respecter la contrainte d'interférence Co - canal,
ie: éviter d'assigner la même fréquence
à deux cellules voisines.
Objectifs :
Trouver un bon plan de fréquence qui doit minimiser
l'ensemble des interférences ainsi que la partie du spectre radio.
3.5.2 Modélisation par la théorie des
graphes
Le probléme d'affectation de fréquences est un
probléme de la classe du coloriage de graphe (Graph Coloring
Problem).
Soit un graphe G = (X, E) defini par:
X: L'ensemble des sommets du graphe représentent les
transmetteurs (TRX).
E: L'ensemble des arêtes du graphe représentent les
risques d'interférences,
Il existe une arête [xi, xj] de E ssi xi est voisin avec x
(voir figure ci-dessous).
Pour résoudre le probléme d'affectation de
fréquences, on utilise la coloration des sommets qui consiste à
affecter à tous les sommets du graphe une couleur (fréquence) de
façon que chaque paire de sommets soit de couleurs differentes; En
d'autre termes, s'il existe une arête [xi, xj] de E alors on a c(i) =6
c(j).
Le nombre minimum de couleurs nécessaires pour colorier
ce graphe en respectant cette contrainte, est appelé le nombre
chromatique XG.
L'application de la théorie des graphes va nous permettre
de trouver le nombre minimal de fréquences allouées aux stations
de bases et qui minimise l'intégralité des
interférences.
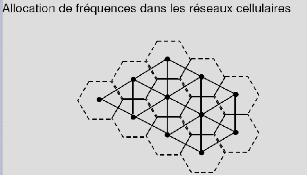
Allocation des fréquences dans les réseaux
cellulaires
3.5.3 Complexité du probléme
Le probléme de la détermination du nombre
chromatique XG est difficile. Plus précisément, déterminer
si un graphe donné à une k-coloration pour un k > 2
fixé est NP-complet .
Notre graphe doit être colorié avec au moins 3
couleurs (la taille de la clique max est égale à w(G) = 3), donc,
il est NP-dure.
Afin de déterminer le nombre chromatique d'un graphe,
un algorithme exact peut être appliqué si la taille du graphe
n'est pas trop grande. Sinon, on se contente d'estimer le nombre chromatique,
en utilisant par exemple un algorithme heuristique telque la Recherche Tabou
qui ne donnera qu'une borne supérieure mais qui est bien plus rapide
qu'un algorithme exact.
3.6 Conclusion
Dans ce chapitre nous avons mis en exergue les
difficultés de la gestion des fréquences, posé la
problématique avec les principaux objectifs assignés à
notre étude et par la même nous avons procédé
à sa modélisation.
Dans le chapitre suivant nous traiterons des méthodes de
résolutions de cette problématique.
| 


