Une description de differentes options exotiques à partir du modèle de Cox Ross et Rubinstein sur quelques periodes

Deuxième partie

Quelques options "path independent"

CHAPITRE 1

LES OPTIONS BINAIRES

1 L'option cash or nothing

Définition 5. L'option cash or nothing permet àl'acheteur de recevoirune prime Q déterminée dans le contrat, lorsque loptionest eexercée, c'est à dire sie cours duous-jacent dépasse K dans le cas d'un call ( et sile cours est en dessous danse cas d'un putt. Le graphique suivant montre le payoff dun tel call, enabscisse S est la valeur du sous jacent à l'échéance.

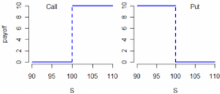
FIG. 1 - Exemple du payoff cash or nothing K=100, Q=10, T=1 an

1.1 Exemple

On veut acheter un call cash or nothing. A t = 0 le cours du sous jacent vaut S = 50 euros. On donne le taux d'intérêt annuel r = 5% ,la date d'échéance T = 6 mois et le nombre de périodes où l'on observe le cours du sous jacent n = 6 . On estime de plus la volatilité annuelle du sous jacent à a = 0, 4. Le vendeur de l'option donne le prix d'exercice à K = 50 et offre une prime de Q = 50. Autrement dit si à la date d'échéance de l'option le sous jacent est supérieur à 50 l'option est exerçable et nous rapportera 50. Dans le cas contraire la somme que l'on aura dépensée pour acheterloption sera perdue.

Nous allons utiliser la méthode de l'arbre binomialOn commence par estimer nos para-

mètres.

0,5 1+ r_n = e^r1n = 1.0042, u_n = eó'4n = 1,1224, d_n = e-ó'1n = 0.8909

T

A_n = n

₆,

d'ou :

p	er1n - e-ó'1n	= 0, 4892 = 1-p = 0, 5108
	eó'1n - e-ó'1n

Nous passons ensuite à l'arbre des valeurs du sous jacent.

Tree Display

At each node:

Upper value = Underlying Asset Price Lower value = Option Price

Values in red are a result of early exercise.

25,008

0

Time step, dt = 0, 0833 years, 30,42 days

Strike price = 50 1,0042

Growth factor per step, a = 1,0042

Discount factor per step = 0,9958

Probability of up move, p = 0,4892

Up step size, u = 1,1224

Down step size, d = 0,8909

15,788

50

23,494

44,547

8,5353

56,12

62,989

2,8164

33,003

39,689

14,579

50

42,799

44,547

70,699

5,7811

35,361

23,89

56,12

0

49,586

79,353

62,989

36,648

39,689

31,505

11,867

50

0

0

49,793

49,793

24,359

44,547

28,069

89,066

70,699

35,361

56,12

0

0

0

62,989

99,967

79,353

39,689

31,505

50

50

50

50

0

0

0

Node Time:

0,0000 0,0833 0,1667 0,2500 0,3333 0,4167 0,5000

FIG. 2 - Evaluation du call cash or nothing dans l'arbre binomial

Lecture de l'arbre On observe les valeurs de St à chaque étape. En noir sont données les valeurs du cours et du call (en dessous) et en rouge les valeurs du payof. On déduit les valeurs des options à chaque période par le principe de rétroduction : la valeur de loption en t = 6 se déduit de (ST -- K)⁺ . On déduit les valeurs précédentes en calculant l'espérance sous probabilité risque neutre que l'on actualise au taux sans risque. On remonte ensuite de la même manière jusqu'en t = 0. On a par exemple la valeur du call après deux montées

1

Cuu = 1+ _r[pCuuu + (1 -- p) Coud]

n