3 Evaluation du call lookback flottant pourr = ó
2
Sous la probabilité risque neutre P l'évolution du
cours du sous jacent est donnée par
|
l'équation :
|
dSt
St
|
= rdt + ódWt
|
où Wt est un P mouvement brownien standard, r le taux
continu sans risque , et ó2 la
variance par unité
de temps. La formule d'Ito admise permet dobtenir pour tout t de [0; T]
|
(St J
ln
S
|
(= r -
|
ó2 J2
|
t + óWt
|
Pour simplifier on se place dans un cas particulier r = ó
2 donc ln (St ) = óWt. Pour évaluer
S
le call loockback de prix d'exercice minSt pour t E 0 = t = T il
nous faut connaître la loi de
|
min
0<t<T
|
St = S min
0<t<T
|
eóWt
|
Pour cela , on va commencer par determiner la loi de minSt pour t
E 0 = t = T. On obtient la relation pour b = a et b = 0
Propriété 1.
J
2b
/
ó T
( J ( -a J ( -a +
P óWT = a et min
0<t<T óWtb = N / - N
ó T
On peut expliquer ce résultat par la
propriété de reflexion du mouvement brownien sur le graphique
suivant où t = 0, W0 = 0 :
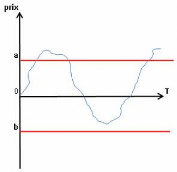
FIG. 5 Encadrement de la trajectoire de St
Démonstration : En effet par le principe de
réflexion du mouvement brownien autour de la droite de "niveau b" on
peut écrire
( ) f-a + 2b
P óWT > a et min
0<t<T óWt b = P (óWT 2b - a) = f './
ó T
Chaque trajectoire (óWt)0 t T, où
óWt a même loi que ó'./t f (0, 1) qui atteint b sur [0, T]
et dépasse a en T, est réfléchie par rapport à cet
axe en une trajectoire qui en T prend une valeur inférieure à 2b
- a. Ce principe est représenté par la figure suivante
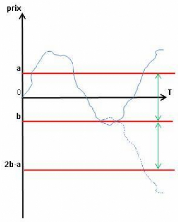
FIG. 6 - Le principe de réflexion du brownien
Si óWT est la trajectoire initiale, alors 2b -- óWT
est la trajectoire réfléchie par rapport à la constante de
niveau b et
óWT = a?2b--óWT < 2b--a <b
Donc
)
2b
v
ó T
( ) (--a +
P óWT = a et min
0<t<T óWt < b = N
D'où puisque
( ) ( )
P óWT = a et min
0<t<T óWt = b + P óWT = a et min
0<t<T óWt < b
=P(óWT = a)
( )
N (0; 1) = a
= P v
ó T
=N
( --a )
v
ó T
On en déduit que pour tout a= b et b = 0:
( J ( --a J
P óWT = a et min
0<t<T óWt = b = N v -- N
ó T
( --a + 2b J
v
ó T
En particulier pour a = b
( J ( J
P óWT = b et min
0<t<T óWt = b = P 0<t<T óWt
= b
min
D'où pour tout b = 0
( J ( --b J ( b
J
P 0<t<T óWt = b
min = N v -- N v
ó T ó T
Le payoff du call lookback est égal à
|
ST -- min
0<t<T
|
St = Seó' T -- S min
0<t<T
|
eó't
|
et la valeur de ce call en 0 est donnée par
( J v
Clookback
0 = e_rT E P ST -- S min
0<t<T eó't T puisque r = ó2
= SN (d1)--SN (--d1) où d1 = ó2
car E (eó'T ) = e ó2 2 Tpuisque W
t est un mouvement brownien et eó'T + ó2 2
t est une martingale.
Exemple Dans notre exemple en maintenant ó = 0,4 il
faudrait avoir r* = 0,16
2= 8%. Ceci permet de garder le même arbre
pour le sous jacentseule la probabilitérisque neutre change:
1, 1224 -- 0,8909
= 0,4989
(1,08)
p=
1 12 --0,8909
Le taux d'actualisation période est r6 = (1,08) 1 12
1,0064. On obtient l'arbre suivant :
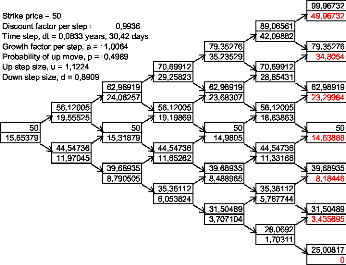
FIG. 7 Call lookback flottant pour r = ó2 2
La formule que nous avons trouvé nous
donneClookback
0 = SN (d1) - SN (-d1), avec
v T = 0, 4v0, 5 = 0, 28284 d'où Clookback
d1 = ó 0 = 50.0, 6113-50.0, 3886 = 11, 13503. Avec
l'arbre on trouve une valeur relativement proche donc un nombre
de périodes un peu plus élevé pourrait nous donner une
bonne approximation
| 


