11 CHAPITRE 2 :
12
13 MODÉLISATION DU SYSTÈME
14 MULTI-MOTEUR (SMM)
15 ET
16 REPRÉSENTATION ÉNERGÉTIQUE
MACROSCOPIQUE (REM)
17
18 1.2. INTRODUCTION
Ce chapitre est consacré à la
présentation et à la modélisation des
Systèmes
Multi-Moteurs (SMM). Le
système de test est constitué de cinq moteurs. Le principe de
fonctionnement de la maquette est décrit et notamment les
problèmes de gestion que peut engendrer un tel système. Les
travaux à effectuer seront mis en évidence. [33,35]
Dans l'industrie du textile ou du papier [33,34], les
systèmes de bobinage sont très présents. Afin de
modéliser le système multi-moteurs étudié, l'outil
utilisé est une représentation appelée
REM : Représentation
Énergétique Macroscopique. Cet
outil développé par le L2EP [27,32] permet d'analyser des
systèmes plus ou moins complexes composés de plusieurs machines
et/ou plusieurs convertisseurs dans des entraînements électriques
et/ou mécaniques. Le contrôle de la vitesse des moteurs consiste
à avoir une vitesse de rotation identique pour chaque moteur, ce qui
permet de faire avancer la toile à une même vitesse.
2.2. MODÉLISATION DU SYSTÈME
MULTI-MOTEUR (SMM)
2.2.1. Structure du système multi-moteur (SMM)
étudié
La figure 2.1 présente un système
d'entraînement constitué de cinq moteurs triphasés, chaque
moteur à une alimentation et commande vectorielle indirect
indépendante IFOC (en
anglais) : Indirect
Field Oriented Control; les
moteurs sont couplés mécaniquement par une bande dont la tension
est réglable par la commande des quatre derniers moteurs. Ce
système est composé de deux parties différentes, la partie
mécanique (Figure 2.1) et la partie électrique (Figure 2.3).
2.2.1.1. Description de la partie mécanique
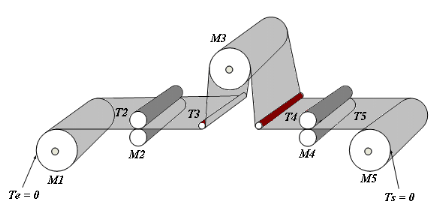
Figure 2.1 : Partie
mécanique du système à cinq moteurs.
Dans la partie mécanique, le moteur M1
effectue le débobinage, M3 entraîne la
toile par friction et M5 sert à effectuer le bobinage,
les moteurs M2 et M4 entraînent chacun
deux rouleaux par l'intermédiaire d'engrenages pour
« pincer » la bande (Figure 2.2). M2 et
M4 pourraient être remplacés par deux moteurs
chacun, qui entraîneraient chacun un rouleau des étages de
pinçage. Les éléments de contrôle de pression entre
les rouleaux ne sont pas représentés, ni considérés
dans l'étude. L'étage de pinçage peut permettre d'isoler
deux zones et de créer une zone tampon. [33,34]
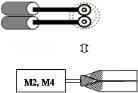
L'objectif de ces systèmes est de maintenir la vitesse
de défilement constante et de contrôler la tension dans la
bande.
Figure 2.2 : Moteur
d'entraînement de l'étage de pincement.
2.2.1.2. Description de la partie
électrique
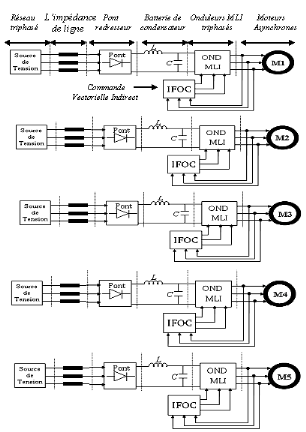
Le banc d'essais est composé de cinq moteurs
asynchrones triphasés; les entraînements sont connectés
chacun à une alimentation triphasée et une IFOC
(Figure 2.3). Les moteurs (M1, M2, M3, M4, M5) sont
alimentés par des onduleurs afin de varier la vitesse. Le
matériau entraîné est considéré comme une
bande élastique. Les moteurs asynchrones utilisés sont
puissants.
Figure 2.3 : Partie
électrique du système à cinq moteurs.
2.2.2. Modèle des principaux
éléments constitutifs du système
2.2.2.1. Modélisation du moteur asynchrone
triphasé
La modélisation du moteur asynchrone a été
abordé en détail dans le chapitre 1.
2.2.2.2. Modélisation de l'enrouleur -
dérouleur
R0
R(t)
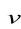
H
Comme on a pu le constater, les divers traitements
s'effectuent en phase de défilement. Il est donc impératif de
disposer d'organes de déroulement et d'enroulement performants. Ces deux
dispositifs, l'enrouleur et le dérouleur, sont symétriques
(Figure 2.4). Après installation sur le moteur dérouleur d'un
rouleau de matière (toile, papier), une bande de produit est sortie et
part vers le reste du processus. Le rôle premier du dérouleur
apparaît ici : l'injection de matière dans le système. Au
cours du cycle de travail, la quantité de matière sur le rouleau
diminue, sa masse et son rayon ne sont donc pas constants. De la même
manière, l'enrouleur récupère le produit traité; au
démarrage, le rouleau porteur est vide, il se remplit au fur et à
mesure de l'avancement. Afin de garantir un enroulement de bonne
qualité, la vitesse linéaire à l'arrivée sur
l'enrouleur doit être constante, l'effort de tension imposé au
matériau également. De même, si on veut assurer un bon
traitement du produit, le dérouleur doit délivrer le produit
à vitesse et tension constantes. Lorsque le dérouleur est vide,
la chaîne doit s'arrêter, le temps de mettre un nouveau rouleau.
Soit l la longueur axiale du roulement de papier. Les
relations cinématiques importantes du roulement de papier peuvent
être développées comme suit (Figure 2.4) [28,31,38,39].
Figure 2.4 : Modèle d'un
rouleau de papier.
Rayon R(t) et masse m : Considérons le
profil du rouleau comme un disque initial de rayon R0 et une couronne de rayon
intérieur  et
extérieur R(t) (Figure 2.4). et
extérieur R(t) (Figure 2.4).
|
(2.1)
|
|
(2.2)
|
|
(2.3)
|
|
(2.4)
|
|
(2.5)
|
Angle de rotation :
Inertie de masse  : De la même manière, on peut
détailler l'inertie : De la même manière, on peut
détailler l'inertie .
Rappelons que l'inertie d'un cylindre creux dépend de ses rayons interne
et externe, de sa masse volumique .
Rappelons que l'inertie d'un cylindre creux dépend de ses rayons interne
et externe, de sa masse volumique  et
de sa hauteur, ici la largeur de la bobine est et
de sa hauteur, ici la largeur de la bobine est  . .
L'inertie d'un rouleau dérouleur ou enrouleur est la
somme de son inertie à vide  (c'est celle de l'arbre moteur) et de l'inertie variable, fonction du rayon
R(t).
(c'est celle de l'arbre moteur) et de l'inertie variable, fonction du rayon
R(t).
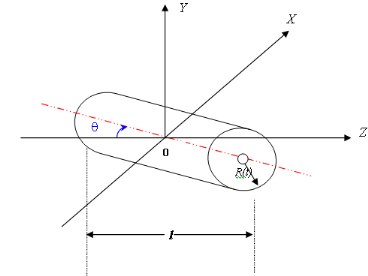
Figure 2.5 : Vue en perspective d'un
rouleau de papier.
Tableau 2.1 :
Paramètres du rouleau de papier.
|
Symbole
|
Signification
|
Unité
|
|
Masse de noyau.
|
kg
|
|
m
|
Masse totale du rouleau de papier.
|
kg
|
|
Rayon du noyau .
|
m
|
|
R
|
Rayon variable de roulement de papier.
|
m
|
|
V
|
Vitesse de défilement du papier.
|
m/s
|
|
H
|
Épaisseur de la feuille de papier.
|
m
|
|
l
|
Longueur longitudinale du rouleau de papier.
|
m
|
|
Densité de masse de la feuille de papier.
|
|
|
Inertie à vide.
|
|
|
Inertie de masse.
|
N m m
|
2.2.2.3.
Modélisation de la toile entre deux rouleaux consécutifs
Les différents modèles pour la toile ou la bande
dans les systèmes de transport de matériaux en feuilles sont
basés sur trois lois [29,37,38].
· La loi de Hooke, qui modèle
l'élasticité du lien entre les enchaînements;
· La loi du coulomb, qui donne la variation de tension
mécanique due au frottement et à la force de contact entre la
toile et le rouleau;
· Loi de conservation de masse, qui exprime
l'interconnexion entre la vitesse de bande et sa contrainte.
Nous présentons ici le développement du
modèle présenté dans [29,30,31].
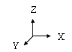
La figure 2.6 montre un système d'enchaînement
entre deux rouleaux avec le repère (X, Y, Z) [30].
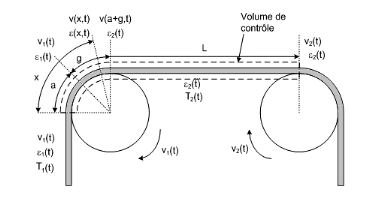
Figure 2.6 : Tension
d'enchaînement entre deux rouleaux.
Pour être plus proche de la réalité, le
modèle mathématique de la bande est développé en
utilisant les hypothèses [30,34,39] suivantes :
· la longueur de la région de contact
(a+g) entre le matériau et le rouleau est très petite
par rapport à celle du matériau au niveau de deux rouleaux,
(L) ce qui permet de définir un volume contrôlé V
(volume des matériau dans la région `g');
· la perte de masse entre le matériau et
l'environnement est supposée négligeable;
· la contrainte dans le matériau entre les deux
rouleaux est uniforme;
· le matériau est isotropique mais c'est la
contrainte le long de l'axe x qui prévaut : x 0,
y = 0 et z = 0;
· la section et la densité du matériau ne
varient pas au cours du temps et sur la longueur du matériau.
· il n'y a pas de glissement entre le matériau et
les rouleaux, la vitesse de défilement du matériau est donc
égale à la vitesse linéaire du rouleau.
La tension d'enchaînement entre deux rouleaux peut
être calculée selon ces trois lois.
La Loi de Hooke : La tension T d'un
enchaînement élastique est fonction de la contrainte
d'enchaînement : [29,39]
Notez que le rapport entre la contrainte et la tension est
plus complexe pour les matériaux viscoélastiques. La loi de Hooke
est valide pour la plupart des matériaux d'enchaînement, aussi
longtemps que la tension n'est pas trop grande.
D'ailleurs, le module de Young est très sensible
à la température et au niveau d'humidité. Sur la
chaîne de production, l'enchaînement peut passer par
différents processus (par exemple, dans un bain dissolvant, puis dans un
dessiccateur). Par conséquent, ses propriétés
d'élasticité peuvent considérablement changer pendant le
processus.
La Loi du Coulomb : L'étude de la
tension d'enchaînement sur un roulement peut être
considérée comme un problème de frottement entre les
solides. Sur le roulement, la tension d'enchaînement est constante sur
une zone de collage qui est un arc de longueur a et change sur une
zone coulissante qui est un arc de longueur g (Figure 2.6). Puis, la
contrainte d'enchaînement entre le premier point de contact d'un
roulement et le premier point de contact du roulement suivant est donné
par les équations suivantes :
|
si 
|
(2.12)
|
|
si 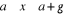
|
(2.13)
|
|
si 
|
(2.14)
|
|
|
(2.15)
|
|
|
Symbole
|
Signification
|
Unité
|
|
Ti (i=1,4)
|
Tension dans le matériau entre chaque paire de
rouleaux.
|
N
|
|
i (i=1,4)
|
Contrainte imposée au matériau.
|
__
|
|
E
|
Module de Young de la bande.
|
N/m²
|
|
S
|
Section d'enchaînement.
|
m²
|
|
L0
|
Longueur nominale d'enchaînement (sans effort).
|
m
|
|
L
|
Longueur d'enchaînement sous l'effort.
|
m
|
|
i (i=1,4)
|
Densité volumique du matériau.
|
kg/m
|
|
Vi (i=1,5)
|
Vitesse linéaire du roulement i.
|
m/s
|
Tableau 2.2 : Définitions et notations
pour l'étude de la toile.
Le changement de tension se produit sur la zone coulissante
tandis que la vitesse d'enchaînement est égale à la vitesse
de roulement sur la zone de collage. Peut également apparaître une
zone coulissante à l'entrée de roulement si la tension change
à un taux élevé.
Loi de Conservation de masse :
Considérez une toile entre deux rouleaux de longueur  avec une densité de poids, sous un effort continu. Supposant que
la section reste constante, puis, selon la loi de conservation de masse, la
masse d'enchaînement reste constante entre l'état sans effort et
l'état sous l'effort : avec une densité de poids, sous un effort continu. Supposant que
la section reste constante, puis, selon la loi de conservation de masse, la
masse d'enchaînement reste constante entre l'état sans effort et
l'état sous l'effort :
Tension d'enchaînement entre deux rouleaux
consécutifs : l'équation de continuité appliquée au
système de transport d'enchaînement donne :
Utilisons l'équation (2.17), que nous intégrons
sur le volume V de commande défini par les premiers points de
contact entre l'enchaînement et les roulements, voir la figure. 2.6.
Supposant que la section d'enchaînement est constante,
 nous pouvons intégrer en ce qui concerne la variable nous pouvons intégrer en ce qui concerne la variable  de
zéro à de
zéro à  . .
Utilisons (2.13)-(2.15), avec l'hypothèse que 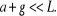
Soit 
  et et
 La relation finale est : La relation finale est :
Cette relation peut être simplifiée en
différenciant la limite gauche.
Puis, en utilisant les approximations.

 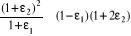
Avec l'équation (2.11), nous obtenons.
Cette relation diffère de celle
présenté dans des études classiques sur des
systèmes d'enroulement. La simplification du modèle classique est
obtenue en employant l'approximation avant de différencier la limite
gauche dans (2.21), ce qui donne l'équation suivante :
Nous pouvons voir que (2.23) donne une meilleure approximation
que (2.24.a). Pour le développement des lois de commande, c'est le
modèle (2.24.a) qui sera employé pour sa simplicité.
2.2.3. Modèle du système multi-moteur
(SMM)
2.2.3.1. Vitesse d'enchaînement sur chaque
roulement
Supposant que l'enchaînement ne glisse pas sur le
rouleau, la vitesse d'enchaînement est égale à la vitesse
linéaire de roulement. L'équation dynamique de la vitesse  du du
 rouleau peut être obtenue par l'équation
d'équilibre de couple : [33,35,36] rouleau peut être obtenue par l'équation
d'équilibre de couple : [33,35,36]
Où  sont les tensions dans le matériau entre chaque paire de rouleaux,
sont les tensions dans le matériau entre chaque paire de rouleaux,  est le somme des couples de frottement. Nous pouvons noter d'après
l'équation (2.25.a) que l'inertie
est le somme des couples de frottement. Nous pouvons noter d'après
l'équation (2.25.a) que l'inertie ,
le rayon ,
le rayon ,
sont liés au temps : ,
sont liés au temps :  et et
 augmentent avec le temps pour l'enrouleur et diminuent avec le temps
pour le dérouleur. Ils peuvent changer considérablement pendant
l'opération de processus complet (environ 300% pour le rayon dans notre
installation expérimentale et encore plus dans quelques systèmes
industriels). augmentent avec le temps pour l'enrouleur et diminuent avec le temps
pour le dérouleur. Ils peuvent changer considérablement pendant
l'opération de processus complet (environ 300% pour le rayon dans notre
installation expérimentale et encore plus dans quelques systèmes
industriels).
2.2.3.2. Modèle complet
Le modèle complet de notre installation
expérimentale peut être établi en utilisant (2.24.a) pour
indiquer la tension mécanique dans chaque segment et (2.25.a) pour
indiquer la vitesse de chaque roulement. La figure 2.7 montre les
différentes variables dans le modèle de notre système
expérimental. Les entrées sont les signaux de commande  (Tensions de commande) et les sorties sont la vitesse linéaire de
défilement et les tensions d'enchaînement, (Tensions de commande) et les sorties sont la vitesse linéaire de
défilement et les tensions d'enchaînement, .
Les signaux de commande sont le couple de référence des moteurs
asynchrones. Traditionnellement, dans un arrangement décentralisé
de commande, la vitesse d'enchaînement est commandée par le moteur
de traction et la tension d'enchaînement est commandée par les
moteurs de déroulement et d'enroulement. Les équations (2.24.a)
et (2.25.a) peuvent être exprimées sous la forme
d'équations d'état : .
Les signaux de commande sont le couple de référence des moteurs
asynchrones. Traditionnellement, dans un arrangement décentralisé
de commande, la vitesse d'enchaînement est commandée par le moteur
de traction et la tension d'enchaînement est commandée par les
moteurs de déroulement et d'enroulement. Les équations (2.24.a)
et (2.25.a) peuvent être exprimées sous la forme
d'équations d'état :
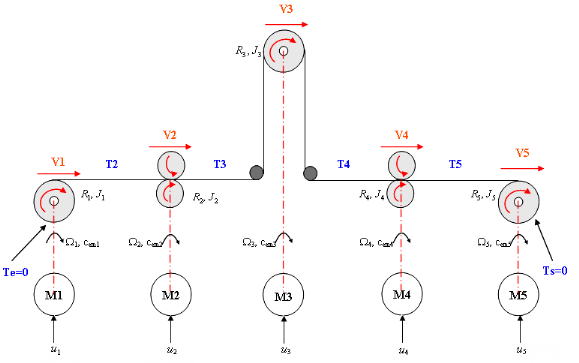
Figure 2.7 : Modèle
complet du système avec cinq moteurs.
2.2.3.3 Équations mécaniques de la
structure complète
Les équations des moteurs et des tensions sont :
 ; ;
et  ;
;
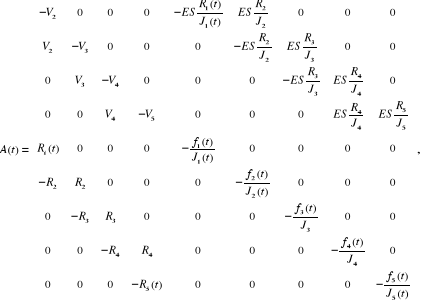


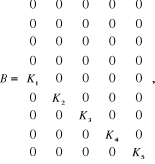
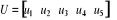
Tableau 2.3 : Paramètres
du modèle complet de cinq moteurs.
|
Symbole
|
Signification
|
Unité
|
|
 (i=1,5)
(i=1,5)
|
Vitesse linéaire du roulement i.
|
m/s
|
|
 (i=1,5)
(i=1,5)
|
Vitesse de rotation du roulement i.
|
rad/s
|
|
 (i=1,5) (i=1,5)
|
Rayon du rouleau i.
|
m
|
|
 (i=1,5) (i=1,5)
|
Moment d'inertie du rouleau i.
|
|
|
 (i=1,5) (i=1,5)
|
Coefficient de frottement visqueux du rouleau . .
|
N.m.s/rad
|
|
 (i=1,4)
(i=1,4)
|
Tension mécanique entre les rouleaux i et
i+1.
|
N
|
|
 (i=1,4) (i=1,4)
|
Longueur d'enchaînement entre les rouleaux i et
i+1.
|
m
|
|
Somme des couples de frottement.
|
N.m
|
|
Matrices diagonales des paramètres.
|
__
|
Les paramètres qui changent pendant le
procédé d'enroulement sont exprimés comme fonction du
temps.
2.3. REPRÉSENTATION ÉNERGÉTIQUE
MACROSCOPIQUE
2.3.1. Définition de la REM
La REM est basée sur le principe d'action et de
réaction et à l'avantage d'offrir une représentation
synthétique. De plus, elle permet aussi de mettre en évidence les
interactions qui existent entre les différents composants d'un
système ainsi que le flux énergétique mis en jeu entre les
divers éléments constitutifs du système. Les informations
contenues dans cette section sont adaptées du rapport [27,32,39].
2.3.2. Éléments de représentation de
la REM
La REM se compose de plusieurs blocs qui ont des formes et
des couleurs normalisées [39], ce qui donne une meilleure
lisibilité de la représentation d'un système (Figure
2.8) :
§ Les sources énergétiques,
représentées par des ovales verts;
§ Les convertisseurs électriques, (des
carrés orange) sans accumulation d'énergie;
§ Les convertisseurs électromécaniques,
(des ronds orange) sans accumulation d'énergie;
§ Les convertisseurs mécaniques, (des triangles
orange) sans accumulation d'énergie;
§ Les éléments accumulant de
l'énergie, (des rectangles orange avec une barre oblique)..etc.
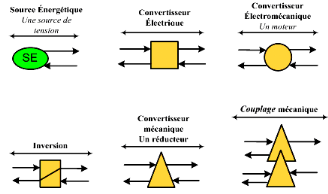
Figure 2.8 :
Éléments de la REM.
2.3.3. Description des éléments de la REM
du système
Pour une meilleure compréhension et une meilleure
lisibilité, la REM est divisée en trois parties. La
première prendra en compte la source d'alimentation triphasée,
l'impédance de la ligne, Le pont redresseur et la batterie condensateur,
la deuxième est la partie électrique du onduleur jusqu'à
la machine asynchrone et la dernière est la partie mécanique qui
représente le couplage entre les moteurs et la toile. La
modélisation est identique pour les cinq moteurs.
2.3.3.1. Modélisation de la première
partie (alimentation)
La première partie (Figure 2.9), qui alimente les cinq
moteurs, est constituée par quatre éléments qui
sont : la source d'alimentation triphasée, l'impédance de
ligne, le redresseur et la batterie condensateur. Cette partie est identique
pour les cinq moteurs
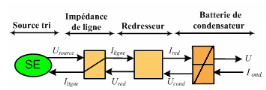
Figure 2.9 : Première
partie du système, source d'alimentation.
2.3.3.1. a . Source
énergétique
La source d'alimentation électrique est de nature
triphasée, on la représente par un élément de
source électrique. Celle-ci nous donne une tension en sortie d'action et
reçoit un courant de ligne en entrée de réaction. C'est le
principe des actions/réactions. Les équations internes du bloc
sont représentées par (2.27.a), (2.27.b) et (2.27.c).
|
(2.27.a)
(2.27.b)
(2.27.c)
|
|
Figure 2.10 : Bloc de source
énergétique.
|
Ua ; Ub ; Uc : les
tensions simples d'une source de tension triphasée
équilibrée.
2.3.3.1. b. Impédance de ligne
L'impédance de ligne est représentée par
un élément d'accumulation, la variable d'état étant
« I ligne». Cette ligne est constituée
d'une résistance R ligne et d'une bobine L
ligne en série pour chaque phase.
|
Avec :
|
|
(2.28)
|
|
Figure2.11 : Bloc
impédance de ligne.
|
Où :
Uentrée =
Usource : la tension d'entrée de
la ligne (qui représente un vecteur).
Uretour = Uredresseur
: la tension d'entrée de réaction.
2.3.3.1. c. Redresseur six diodes
Ce redresseur triphasé est constitué de six
diodes. Il est représenté par un élément de
conversion électrique. Ce pont ne peut pas être commandé.
Il n'y a donc pas de degré de liberté et ainsi pas de
possibilité de réglage.
|
 Figure 2.12 : Bloc redresseur six
diodes. Figure 2.12 : Bloc redresseur six
diodes.
|
|
|
2.3.3.1. d. Batterie de condensateur
Cette batterie placée entre le redresseur et les
onduleurs de chaque moteur. On peut alors caractériser cette liaison par
un élément d'accumulation avec un couplage électrique, la
variable d'état étant la tension de sortie« U
».
|
|
(2.29)
|
|
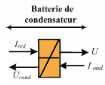
Figure 2.13 : Bloc batterie de
condensateur.
|
Avec : C : condensateur du bus
continu ; Rcond : résistance de fuite en
parallèle avec le condensateur ; i
entrée = i red : courant d'entrée du
condensateur; i retour = I ond courant
d'entrée de réaction.
2.3.3.2. Modélisation de la deuxième
partie (moteur-électrique)
Cette partie électrique est constitué par trois
éléments qui sont : l'onduleur, le stator de la machine
asynchrone (MAS) et la machine elle même (figure 2.14). Cette partie est
identique pour les cinq moteurs. Pour l'action et réaction entre la
première et la deuxième partie, la tension de sortie d'action
étant la même pour les cinq onduleurs, on peut considérer
comme une source électrique qui délivre une tension U,
le courant Iond étant le courant de
retour de l'onduleur triphasé.
|
|
Figure 2.14 : Deuxième
partie du système, partie électrique.
|
2.3.3.2. a. Onduleur Triphasé
L'onduleur est représenté par un convertisseur
électrique.
|
|
Figure 2.15 : Bloc d'onduleur
triphasé.
|
2.3.3.2. b. Stator de moteur asynchrone
Le stator de la machine asynchrone peut être
représenté par la mise en série d'une résistance et
d'une bobine où le courant I stator est commun. On
représente alors cet élément par un élément
d'accumulation avec comme variable d'état le courant I stator
, l'entrée de réaction étant la force
électromotrice du moteur.
|

Figure 2.16 : Bloc de
stator.
|
2.3.3.2. c. Machine asynchrone MAS
La MAS est représentée par un
élément de conversion électromécanique. Elle permet
d'obtenir un couple à partir d'un courant. La sortie de
réaction : la force électromotrice est obtenue par
l'entrée de réaction qui est la vitesse angulaire. Il faut savoir
que pour les simulations, la machine est représentée par
l'intermédiaire du modèle de Park et les
équations de la machine asynchrone. On suppose ainsi que l'onduleur
fournit une tension triphasée équilibrée.
|

Figure 2.17 : Bloc de machine
asynchrone MAS.
|
2.3.3.3. Modélisation de la troisième
partie (couplage mécanique)
La troisième partie est la partie mécanique
(Figure 2.18) qui représente la modélisation des arbres des
moteurs, les différentes toiles et le couplage mécanique. Ce
couplage permet entre autre d'exprimer la vitesse linéaire d'un moteur
par l'intermédiaire de sa vitesse angulaire et du rayon du rouleau. Les
éléments de même nature ne seront étudiés
qu'une seule fois car ils sont basés sur le même principe.
L'exemple pris est celui de l'entraînement en forme
générale.
Figure 2.18 : Troisième
partie du système, partie mécanique.
2.3.3.3. a. Arbre du moteur
L'arbre est caractérisé par son inertie. Les
interactions qui peuvent exister entre cet arbre et sa charge sont aussi prises
en compte. La vitesse est une variable d'état, cet élément
est alors représenté par un élément
d'accumulation.
|
|
(2.30)
|
|

Figure 2.19 : Bloc arbre de
moteur.
|
2.3.3.3. b. Conversion des vitesses et
forces/couples
Le couplage mécanique permet de réaliser une
conversion; on exprime la vitesse linéaire du moteur par
l'intermédiaire de sa vitesse angulaire en la multipliant par le rayon
de l'arbre. Dans notre cas nous prenons le rayon du rouleau accouplé
à l'arbre, on considère que la liaison entre les rouleaux et les
arbres est parfaite. De même pour le couple résistant, on
l'exprime à partir de la force qui est appliquée à la
roue.
|
|
(2.31)
(2.32)
|
|

Figure 2.20 : Bloc conversion
des vitesses et forces/couples.
|
2.3.3.3. c. Couplage entre moteurs
Le moteur MK+1 a une liaison avec les
moteurs MK et MK+2 par
l'intermédiaire de la toile. Il y a donc un couplage de type
mécanique. En effet, la sortie de réaction VK+1
est commune aux entraînements MK et
MK+2 (2.33). On s'aperçoit aussi que le couple
résistant dépend de deux variables : TK+1
et TK+2 (2.34).
|
|
(2.33)
(2.34)
|
|

Figure 2.21 : Bloc de couplage
entre moteurs (étage k+1).
|
2.3.3.3. d. Toile
La toile est considérée comme un matériau
élastique. Celle-ci est représentée par un
élément d'accumulation avec comme variable d'état la
tension. Celle-ci dépend de la vitesse des moteurs.
La tension d'entrée Te du premier moteur (bobineur) et
la tension de sortie Ts du dernier moteur (débobibeur) ne sont pas
prises en considération dans l'étude du modèle
général de la toile (2.35).
|
|
(2.35)
|
|

Figure 2.22 : Bloc de la toile
(segment k+1).
|
2.3.4. Représentation complète du
système cinq moteurs par REM
On peut s'apercevoir qu'une fois le système
modélisé, beaucoup de variables sont mises en jeu, et que la
gestion d'un tel système ne soit pas simple. En effet, la
présence de couplages et le partage de variables communes peuvent
entraîner des perturbations. La modélisation de chaque
élément de la maquette a été
présentée dans le paragraphe {§2.2.3}, la
modélisation complète du système est
représentée dans la figure 2.23.
|
|
Figure 2.23 :
Représentation complète du système cinq moteurs par
REM.
|
2.4. CONCLUSION
À travers ce chapitre une étude
détaillée de la modélisation des systèmes
multi-moteurs (SMM) et la structure du système ont été
développées. Dans la partie de la modélisation du moteur
asynchrone ses équations sont explorées en détail
(Chapitre 1). Ces dernières sont obtenues pour les systèmes
électrique et mécanique. Par la loi de Hook, les calculs de la
tension d'enchaînement entre deux moteurs sont développés.
Ces calculs permettent l'obtention des tensions mécaniques entre une
série des moteurs d'entraînement. Finalement, l'utilisation de la
modélisation obtenue dans ce chapitre, permet d'avoir un système
matriciel sous la forme d'équations d'état. Ce dernier sera
utilisé dans le chapitre III.
Afin de modéliser le système multi-moteur
étudié, l'outil que nous avons utilisé est une
représentation appelée Représentation
Énergétique Macroscopique (REM). Cet outil,
développé par le Laboratoire d'Électrotechnique et
d'Électronique de Puissance de Lille (L2EP), permet d'analyser des
systèmes complexes composés de plusieurs machines et plusieurs
convertisseurs dans des entraînements électriques et
mécaniques. La REM est basée sur le principe d'action et de
réaction et à l'avantage d'offrir une représentation
synthétique des systèmes énergétiques. Elle permet
aussi de mettre en évidence les interactions qui existent entre les
différents composants d'un système ainsi que le flux
énergétique mis en jeu entre les divers éléments du
système.
| 


