7 CHAPITRE 1
:
8 9 MODÉLISATION ET
COMMANDE
10 VECTORIELLE DE LA MACHINE ASYNCHRONE
1.1. INTRODUCTION
Les équations de Park ont été et sont
encore la référence pour l'élaboration du modèle de
connaissance traduisant le comportement dynamique des modes électriques
et électromagnétiques de la machine. Même si, actuellement,
certains travaux sont réalisés pour affiner ces équations
(prise en compte des effets de saturation magnétique), le modèle
de Park, décrit par un système algébro-différentiel
non linéaire, reste toujours pour l'automaticien le modèle le
plus intéressant par rapport aux différentes classes de
représentations d'état qu'il permet d'exprimer. En effet, selon
le type de commande que l'on veut réaliser : couple, vitesse,
position, selon la nature de la source d'alimentation (tension ou courant), du
référentiel de travail ((á,â), (d,q)), et enfin des
composantes du vecteur d' état (flux ou courants statoriques ou
rotoriques), différents modèles d'états peuvent être
formulés.
Au début des années 70, Blaschke et Hasse ont
donné naissance à une nouvelle technique dite commande
vectorielle. Par cette technique, la machine asynchrone (MAS) peut avoir les
mêmes propriétés avec la machine à courant continu
(MCC), sans les inconvénients liés au système
balais-collecteur [1,2,3]. Les travaux de recherche effectués sur ce
sujet utilisent une des principales trois méthodes, qui la
deuxième. La première dite « méthode
directe », a été initiée par Blaschke [2], la
deuxième dite « méthode indirecte » a
été introduite par Hasse [4] et la troisième dite
« méthode simplifiée » est
développée par Robyns sur une machine alimentée en tension
dont le rôle est de linéariser le comportement de la machine
[5].
Dans ce chapitre, nous présentons la
modélisation de la machine asynchrone en mettant l'accent sur sa
représentation d'état liée aux entrées et sorties
du moteur. Nous donnons aussi un aperçu sur la commande vectorielle
appliquée à une machine asynchrone alimentée en tension.
La méthode obtenue dans la suite de notre travail est
la méthode indirecte, dans cette méthode, et pour le
réglage du courant et de la vitesse nous avons utilisé un
contrôleur conventionnel Proportionnel - Intégral (PI).
1.2. MODÉLISATION DE LA MACHINA ASYNCHRONE
1.2.1. Principe de fonctionnement de la
MAS
Le moteur à induction se comporte comme un
transformateur à couplage par champ tournant et à secondaire en
court-circuit. Les terminologies utilisées pour une machine asynchrone
se rapprochent donc de celles utilisées dans l'étude des
transformateurs [11,14]. Le primaire alimenté par des courants à
la pulsation  crée un champ tournant à la vitesse synchrone
crée un champ tournant à la vitesse synchrone  où
où  désigne le nombre de paires de pôles de la machine. Ce champ
balaie le rotor de sorte que les enroulements secondaires sont traversés
par un flux variable. Celui-ci est à l'origine de f.e.m (forces
électromotrices) induites. Les courants qui en résultent donnent
naissance à un moment magnétique qui, sous l'action du champ
primaire, provoque l'apparition d'un couple électromagnétique. Si
le rotor tourne à la vitesse synchrone, le flux à travers le
secondaire ne varie plus, donc il n'y a pas de f.e.m induites, donc de couple.
[11]
désigne le nombre de paires de pôles de la machine. Ce champ
balaie le rotor de sorte que les enroulements secondaires sont traversés
par un flux variable. Celui-ci est à l'origine de f.e.m (forces
électromotrices) induites. Les courants qui en résultent donnent
naissance à un moment magnétique qui, sous l'action du champ
primaire, provoque l'apparition d'un couple électromagnétique. Si
le rotor tourne à la vitesse synchrone, le flux à travers le
secondaire ne varie plus, donc il n'y a pas de f.e.m induites, donc de couple.
[11]
Le moteur tourne à une vitesse  d'autant plus inférieure à
d'autant plus inférieure à  que
le couple développé est important, puisque la variation du flux,
donc des f.e.m et des courants du secondaire, est liée à la
vitesse relative que
le couple développé est important, puisque la variation du flux,
donc des f.e.m et des courants du secondaire, est liée à la
vitesse relative  . En
général, cette différence de vitesse relative est
évaluée par le glissement [14] : . En
général, cette différence de vitesse relative est
évaluée par le glissement [14] :
1.2.2. Hypothèses simplificatrices pour la
modélisation
La machine asynchrone étant un système dynamique
non linéaire, il est nécessaire de disposer d'un modèle
représentant fidèlement son comportement au niveau de ses modes
électriques, électromagnétique et mécanique. Dans
la littérature de la « commande », le modèle
de Park est généralement choisi. En effet, c'est une solution qui
tient compte d'une part des qualités demandées par la commande et
qui d'autre part prend en compte des hypothèses simplificatrices
intrinsèques au système.
Nous nous plaçons dans le cas d'une machine asynchrone
triphasée et symétrique dont le rotor est à cage. Les
hypothèses permettant de mettre en place le modèle de Park sont
les suivantes [14] :
§ Le circuit magnétique est non
saturé ;
§ L'entrefer est parfaitement lisse ;
§ La densité du courant est uniforme dans les
conducteurs élémentaires ;
§ Les pertes dans le fer sont négligeables.
1.2.3. Modélisation
électrique
La machine asynchrone est de nature triphasée. La
structure symétrique et équilibrée de la machine permet de
passer à une représentation biphasée équivalente
(transformation de Park), réduisant considérablement la
complexité du modèle en vue de la commande. Toutes les grandeurs
électromagnétiques (flux, courants) soient statoriques ou
rotoriques sont ramenées sur un seul repère. Ce repère
peut être positionné soit fixe par apport au stator (repère
á-â), soit tournant (repère d-q)). Un repère
tournant implique la présence d'une variable supplémentaire qui
permet de définir la position de ce repère.
1.2.3.1. Équations générales du
modèle biphasé de la machine asynchrone
Dans le cas d'un repère tournant et après
transformation de Park [9,10], les équations de la machine sont
données de manière générale par les
équations ci-dessous (dans ce modèle, toutes les grandeurs
sont ramenées dans le repère d-q): [6,7,8] :
|
(1.2)
|
|
(1.3)
|
|
(1.4)
|
|
(1.5)
|
|
(1.6)
|
|
(1.7)
|
|
(1.8)
|
|
(1.9)
|
|
Avec :
|
|
|
(1.10)
|
|
(1.11)
|
La vitesse mécanique est donnée par  où
où  est
le nombre de paires de pôles. est
le nombre de paires de pôles.  donne la vitesse angulaire du repère d-q tournant. La différence
entre
donne la vitesse angulaire du repère d-q tournant. La différence
entre  et et  est
la vitesse de glissement est
la vitesse de glissement . Le
repère á-â n'est qu'un cas particulier du repère d-q
en prenant . Le
repère á-â n'est qu'un cas particulier du repère d-q
en prenant  nulle.
nulle.
1.2.3.2. La représentation d'état du
modèle avec entrées en tension de la MAS
Nous étudions ici la classe des objectifs relative au
contrôle de la vitesse ou de la position sous l'hypothèse d'un
fonctionnement à flux constant, ce choix représente en effet
(avec le contrôle du couple [10]) la majorité des applications de
commande de la machine asynchrone dans le domaine industriel à vitesse
variable.
Ces objectifs imposent donc directement le choix des sorties
du système. La représentation d'état du moteur
dépend, comme nous l'avons vu, du repère choisi et du choix des
variables d'état du modèle s'il est avec entrées en
tension où avec entrées en courant [11,12,13] pour les
équations électriques. Nous donnons, dans ce chapitre, dans la
suite de cette thèse, une classe de modèle (modèle avec
entrées en tension) de la machine asynchrone qui sera exploitée
pour la mise au point de nos lois de commande.
1.2.3.2.a. Choix des variables
d'état
Le choix des variables d'état dépend des
objectifs liés soit à la commande soit à l'observation.
Pour le modèle complet, la vitesse mécanique, dont on veut
contrôler l'évolution, est une variable d'état. Nous
considérons dans notre cas les variables d'état
suivants :
Ce choix de variables se justifie d'une part par le fait que
les courants statoriques sont mesurables et d'autre part parce que l'on veut
réguler la norme du flux rotorique. Bien entendu, d'autres choix
associant uniquement les courants ou les flux statoriques et rotoriques sont
possibles. Les entrées du modèle de la machine asynchrone sont
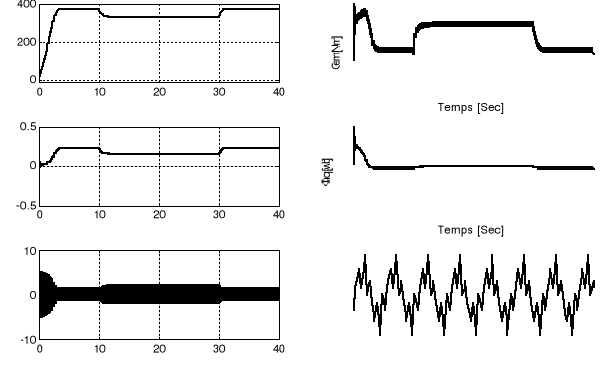
les tensions de commande  , ,
 . .
Pour mettre les équations sous forme de
représentation d'état, nous devons modifier les équations
des tensions statoriques (1.6), (1.7) afin d'exprimer les flux  et et
 en fonction des variables d'état : en fonction des variables d'état :  , , , , et et
 . En considérant les équations des flux (1.2)-(1.5) et en
introduisant le coefficient de dispersion magnétique . En considérant les équations des flux (1.2)-(1.5) et en
introduisant le coefficient de dispersion magnétique , on
trouve les composantes du flux statorique : , on
trouve les composantes du flux statorique :
Et leurs dérivées :
En remplaçant dans les équations des tensions
rotoriques (1.8), (1.9) les courants rotoriques  et et
 par les équations (1.2)-(1.5), on obtient : par les équations (1.2)-(1.5), on obtient :
Les équations des tensions statoriques (1.6), (1.7)
prennent donc la forme :
En introduisant les définitions suivantes :
Ces quatre dernières équations (1.17)-(1.20)
permettent d'obtenir la mise en forme matricielle de la représentation
d'état :
A ces équations électriques, nous devons
associer le vecteur de sorties  ainsi que l'équation mécanique pour obtenir le modèle
complet. Les sorties du modèle que l'on considérera seront dans
notre cas, et dans un premier temps, la vitesse mécanique et la norme du
flux rotorique ; dans un deuxième temps, la position
mécanique et la norme du flux rotorique. Concernant les sorties
citées, la vitesse mécanique est mesurable par des
tachymètres ou par l'intermédiaire de la position à l'aide
des codeurs incrémentaux. Si le couple est choisi comme sortie, celui-ci
peut être mesuré à l'aide de couplemètres
mécaniques posés sur l'arbre de la machine. Cependant, pour une
question de coût, ces appareils de mesure ne sont pas toujours
disponibles pour l'industriel, le corollaire est alors une demande de commande
de moteur sans capteur. La deuxième sortie, la norme du flux rotorique
est généralement choisie constante en fonction de deux
considérations fondamentales :
ainsi que l'équation mécanique pour obtenir le modèle
complet. Les sorties du modèle que l'on considérera seront dans
notre cas, et dans un premier temps, la vitesse mécanique et la norme du
flux rotorique ; dans un deuxième temps, la position
mécanique et la norme du flux rotorique. Concernant les sorties
citées, la vitesse mécanique est mesurable par des
tachymètres ou par l'intermédiaire de la position à l'aide
des codeurs incrémentaux. Si le couple est choisi comme sortie, celui-ci
peut être mesuré à l'aide de couplemètres
mécaniques posés sur l'arbre de la machine. Cependant, pour une
question de coût, ces appareils de mesure ne sont pas toujours
disponibles pour l'industriel, le corollaire est alors une demande de commande
de moteur sans capteur. La deuxième sortie, la norme du flux rotorique
est généralement choisie constante en fonction de deux
considérations fondamentales :
§ La première est liée à la
facilité de la commande puisque le couple est alors régulé
uniquement par un courant 
§ La seconde est liée aux performances dynamiques
qui sont meilleurs puisque le couple est proportionnel à un courant.
1.2.3.2.b. Le couple électromagnétique
de la machine asynchrone
Le couple électromagnétique  développé par la machine peut s'exprimer de différentes
façons qui dépendent de la stratégie de commande
adoptée.
développé par la machine peut s'exprimer de différentes
façons qui dépendent de la stratégie de commande
adoptée.
Du point de vue de l'état et de par le choix de nos
variables d'état, le couple de la machine est donné par le
produit vectoriel suivant :
Avec :  indique le produit vectoriel. indique le produit vectoriel.
Cette expression de couple sera celle utilisée pour
écrire le modèle final de la machine sous forme de
représentation d'état.
1.2.3.2.c. Modèle final de la machine
asynchrone
A l'équation du couple électromagnétique
(1.24) s'ajoute l'équation mécanique :
Où  représente le couple résistant du aux frottements ainsi
qu'à la charge de la machine,
représente le couple résistant du aux frottements ainsi
qu'à la charge de la machine,  est l'inertie de l'ensemble tournant.
est l'inertie de l'ensemble tournant.
L'équation (1.25) peut aussi s'écrire :
Avec :
 : le couple de charge ; : le couple de charge ;
 : le coefficient du frottement sur l'arbre. : le coefficient du frottement sur l'arbre.
En utilisant les notations (1.21), le modèle non
linéaire complet de la machine asynchrone est donné par :
Avec :
 ,
,
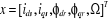
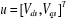
|
 et et
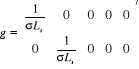
|
(1.29)
|
1.2.4. Commande de l'onduleur par Modulation de
Largeur d'Impulsion (MLI)
L'onduleur a pour objectif de produire des tensions
alternatives variables en amplitude et en fréquence, en fonction des
caractéristiques électromagnétiques
désirées. Une principale stratégie peut être mise en
oeuvre [6,14,15] et retenue dans la suite de notre travail, c'est la
méthode de contrôle par modulation de largeur d'impulsion
(MLI).
Figure 1.1 : Principe de la commande
à MLI.
Commande des interrupteurs
Bras d'un onduleur
Porteuse
Modulateur
Régulateur
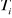
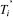
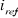
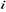
-
La méthode consiste à imposer aux bornes de la
machine des créneaux de tension de manière à ce que le
fondamentale de la tension soit le plus proche de la référence.
Plusieurs techniques sont réalisables pour la modulation de largeur
d'impulsion [14,16,18,19]. La technologie la plus utilisée consiste
à comparer un signal triangulaire (porteuse) avec un signal de
référence, l'intersection des deux signaux définit les
instants de commande des interrupteurs (figure 1.1).
On définit l'indice de modulation  comme le rapport de la fréquence
comme le rapport de la fréquence  de
la porteuse à la fréquence de
la porteuse à la fréquence  de
la tension de référence. Le taux de modulation de
la tension de référence. Le taux de modulation  est le rapport de l'amplitude
est le rapport de l'amplitude  de
la tension de référence à l'amplitude de
la tension de référence à l'amplitude  de
la porteuse. de
la porteuse.
L'association de l'onduleur à MLI avec la MAS est
schématisée par la figure 1.2, les tensions de
référence sont calculées par une transformation de
coordonnées.
Figure 1.2 : Association de
l'onduleur à MLI avec la MAS.
dq
abc
Onduleur
MAS
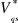
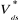
Commande à
MLI
La simulation de l'ensemble MAS dont les paramètres
sont donnés dans l'annexe (1) et l'onduleur à MLI a
été faite sous les conditions de fonctionnement suivantes avec un
temps de simulation de  : :
§ Démarrage à vide;
§ A l'instant  application d'une charge de
application d'une charge de  ; ;
§ A  élimination de la charge.
élimination de la charge.
On remarque que la duré de régime transitoire
4.4 sec, et que la vitesse se diminue avec l'augmentation de la charge et puis
elle augmente avec sa diminution, d'autre part le couple
électromagnétique  suit la valeur du couple résistant. On note aussi une oscillation au
niveau du courant
suit la valeur du couple résistant. On note aussi une oscillation au
niveau du courant  et
du couple obtenus avec la commande MLI. Le courant de phase est chargé
d'harmonique ceci peut être justifié par la grande
fréquence de la charge de l'onduleur. et
du couple obtenus avec la commande MLI. Le courant de phase est chargé
d'harmonique ceci peut être justifié par la grande
fréquence de la charge de l'onduleur.
La figure 1.3 décrit les résultats obtenus avec
la commande MLI :
Figure 1.3 : Comportement dynamique
de la MAS associée
à un onduleur à MLI
1.3. LA COMMANDE VECTORIELLE DE LA MACHINE
ASYNCHRONE
1.3.1. Principe de la commande vectorielle
L'algorithme de référence de commande de la
machine asynchrone est la commande à flux orienté
(Field Oriented Control) a
été mis au point par Blaschke en 1972 [4]. Cette méthode a
marqué un pas décisif dans la façon de concevoir la
commande des machines à courant alternatif. En effet, jusqu'aux
développements théorique et pratique de Blaschke, seule la
commande scalaire était utilisée. A partir du constat que la
machine à courant continu était commandée via un
découplage naturel, l'idée fondamentale de Blaschke fut de mettre
au point une commande permettant de ramener le comportement de la machine
asynchrone à celui de la machine à courant continu. Cette
méthode se base sur la transformation des variables électriques
vers un référentiel qui tourne avec le vecteur du flux rotorique.
Par conséquent, ceci permet de commander le flux de la machine avec un
courant  qui est l'équivalent du courant inducteur de la machine à courant
continu. A condition de travailler à flux constant, un courant
orthogonal
qui est l'équivalent du courant inducteur de la machine à courant
continu. A condition de travailler à flux constant, un courant
orthogonal  permet de contrôler le couple
électromagnétique, correspondant au courant induit de la machine
à courant continu. permet de contrôler le couple
électromagnétique, correspondant au courant induit de la machine
à courant continu.
Trois méthodes de commandes vectorielles sont
possibles : la commande vectorielle directe où l'on estime la norme
et la position du flux rotorique, la commande vectorielle indirecte qui estime
uniquement la position du flux rotorique et la commande vectorielle
simplifiée qui sert à linéariser le modèle de la
machine asynchrone et le rendre similaire à celui d'une machine à
courant continu à excitation séparée.
1.3.2. Equations dans le repère d-q
Nous avons vu que le couple en régime transitoire
s'exprime dans le repère d-q comme un produit croisé de courants
ou de flux. Si nous reprenons l'écriture :
On s'aperçoit que si on élimine le
deuxième produit  ,
alors le couple ressemble à celui d'une machine à courant
continu. Donc, il suffit d'orienter le repère d-q de manière
à annuler la composante de flux en quadrature. C'est-à-dire, de
choisir convenablement l'angle de rotation de Park de sorte que le flux
rotorique soit entièrement porté sur l'axe direct d et donc avoir ,
alors le couple ressemble à celui d'une machine à courant
continu. Donc, il suffit d'orienter le repère d-q de manière
à annuler la composante de flux en quadrature. C'est-à-dire, de
choisir convenablement l'angle de rotation de Park de sorte que le flux
rotorique soit entièrement porté sur l'axe direct d et donc avoir
 et et  (Figure 1.4).
(Figure 1.4).
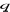
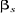
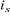
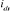
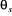
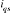
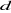
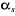
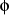
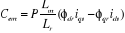
= 0
Figure 1.4 : Principe
d'orientation du flux rotorique.
A partir de là, le modèle de la machine (1.27)
s'écrit :
|
(1.31)
|
|
(1.32)
|
|
(1.33)
|
|
(1.34)
|
|
(1.35)
|
En utilisant l'opérateur transformé de
Laplace ,
l'équation (1.33), peut être réécrite : ,
l'équation (1.33), peut être réécrite :
D'autre part, à partir de l'équation (1.35), le
couple électromagnétique est donné par :
Donc à flux  constant, la composante
constant, la composante  commande le flux rotorique et la composante
commande le flux rotorique et la composante  commande le couple électromagnétique, c'est pourquoi on parle de
découplage dans la commande vectorielle.
commande le couple électromagnétique, c'est pourquoi on parle de
découplage dans la commande vectorielle.
Notons que le problème essentiel de la commande est de
déterminer la norme et la position du flux rotorique, qui ne sont pas
mesurables directement. Il est nécessaire de connaître ces deux
grandeurs pour le contrôle du régime dynamique de la machine. Dans
la suite, la méthode indirecte de la commande vectorielle va être
présentée.
1.3.3. Commande vectorielle indirecte
La méthode indirecte consiste à ne pas estimer
l'amplitude du flux rotorique mais à utiliser directement l'amplitude de
référence .
L'intérêt de cette méthode est d'utiliser uniquement des
grandeurs de référence qui par définition ne sont pas
bruitées. En effet, à partir d'un couple
électromagnétique de référence .
L'intérêt de cette méthode est d'utiliser uniquement des
grandeurs de référence qui par définition ne sont pas
bruitées. En effet, à partir d'un couple
électromagnétique de référence  et
du flux rotorique de référence et
du flux rotorique de référence ,
les courants de références ,
les courants de références  et et
 s'en déduisent directement grâce aux équations
(1.36), (1.37) [17,22,23,24,25,26] : s'en déduisent directement grâce aux équations
(1.36), (1.37) [17,22,23,24,25,26] :
Pour l'équation (1.34), avant l'intégration, il
est nécessaire de souligner que pour maintenir le flux  nul, il faut imposer
nul, il faut imposer ,
on obtient alors : ,
on obtient alors :
On peut obtenir la position du repère par
intégration de l'équation (1.40) sachant d'une part que la mesure
de la position mécanique  est nécessaire et d'autre part que la composante
est nécessaire et d'autre part que la composante  correspond à la référence, c'est-à-dire
correspond à la référence, c'est-à-dire  . .
La méthode de commande indirecte se caractérise
donc par le fait qu'aucune estimation du flux n'est nécessaire, le
contrôle vectoriel est alors simplifié. La méthode repose
en fait en grande partie sur la capacité de l'onduleur et de sa commande
à imposer les courants désirés dans la machine. En effet,
à partir de l'instant où le système n'impose pas les
courants désirés, cette commande perd sa principale
propriété de découplage entre flux et couple. Cette
méthode consiste à générer à l'aide d'un
bloc IFOC (Indirect Field
Oriented Control), les tensions
d'alimentation afin d'obtenir un flux et un couple désirés.
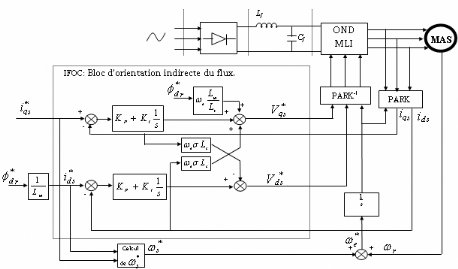
Le schéma de principe de la loi de commande vectorielle
indirecte est présenté dans la figure 1.5 [6, 20,21].
Figure 1.5 : Schéma de
principe de la commande vectorielle indirecte.
Le bloc de contrôle IFOC (génère les trois
grandeurs de commande  , ,
 et et  en
fonction des deux entrées de référence ( en
fonction des deux entrées de référence ( , ,
 ) qui assurent le découplage. ) qui assurent le découplage.
Dans cette commande l'angle  utilisé dans les transformation de Park est calculé par :
utilisé dans les transformation de Park est calculé par :
Ces grandeurs de commande générées par le
IFOC sont utilisées pour contrôler les composants : direct
 et quadratique et quadratique  du
courant statorique de façon à obtenir des courants identiques aux
courants de référence, et par conséquent, le flux et le
couple maintenus à leurs valeurs de référence. du
courant statorique de façon à obtenir des courants identiques aux
courants de référence, et par conséquent, le flux et le
couple maintenus à leurs valeurs de référence.
Le calcul des régulateurs est effectué à
l'aide du principe d'imposition des pôles.
1.3.3.1. Calcul des régulateurs
1.3.3.1.a. Régulateur du courant 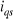
Le régulateur du courant en quadrature fournit la
tension  nécessaire pour maintenir le couple à sa valeur de
référence. La fonction de transfert
nécessaire pour maintenir le couple à sa valeur de
référence. La fonction de transfert  est donnée par :
est donnée par :
Avec :
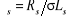
La boucle de régulation du courant est
représentée par la figure 1.6.
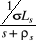
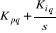
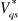
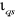
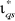
-
+
Figure 1.6 : Schéma de
régulation du courant . .
La fonction de transfert en boucle fermée est
donnée comme suit :
L'équation caractéristique est du
deuxième ordre, donc en imposant deux pôles complexes
conjugué à partir réelle négative  d'ou :
d'ou :
Par identification, nous obtenons les paramètres du
régulateur PI :
1.3.3.1.b. Régulateur du courant 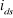
Le régulateur du courant direct fournit la tension  nécessaire pour maintenir le flux à sa valeur de
référence.
nécessaire pour maintenir le flux à sa valeur de
référence.
La fonction de transfert  est donnée par :
est donnée par :
Les mêmes calculs effectués pour le
régulateur du courant  sont appliqués à ce régulateur. Les paramètres du
régulateur sont donc les mêmes et Il sont donnés
par :
sont appliqués à ce régulateur. Les paramètres du
régulateur sont donc les mêmes et Il sont donnés
par :
1.3.3.1.c. Calcul du régulateur de
vitesse
Le régulateur de vitesse permet de déterminer le
couple de référence, a fin de maintenir la vitesse
correspondante. Pour que la cascade soit justifiée, il faut que la
boucle interne soit très rapide par rapport à celle de la
vitesse.
L'équation mécanique donne :
Le schéma bloc de régulation de la vitesse est
indiqué par la figure 1.7.
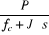
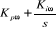
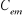
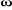
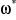
-
+
Figure 1.7 : Schéma bloc
de régulation du la vitesse.
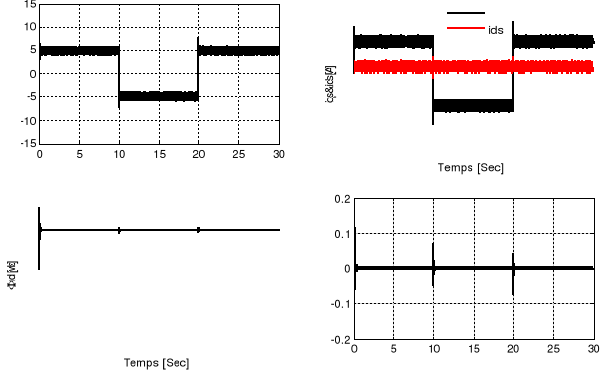
La fonction de transfert en boucle fermée est
donnée par :
L'équation caractéristique  est :
est :
Par imposition de deux pôles complexes conjugués
 en boucle fermée et par identification, on obtient les
paramètres du régulateur PI : en boucle fermée et par identification, on obtient les
paramètres du régulateur PI :
1.3.3.2. Test de découplage
Pour tester l'efficacité du découplage à
l'aide du bloc IFOC une simulation des flux  et et
 , du couple et des courants , du couple et des courants  , ,
 est présentée dans la figure 1.8. Les testes de
simulation ont été faite en injectant un couple
électromagnétique de référence est présentée dans la figure 1.8. Les testes de
simulation ont été faite en injectant un couple
électromagnétique de référence  =
5N.m, à l'instant t = 10sec, =
5N.m, à l'instant t = 10sec,  =
-5N.m et a l'instant t = 20sec, =
-5N.m et a l'instant t = 20sec,  =
5N.m, le flux de référence =
5N.m, le flux de référence  =
0.55Wb. Les résultats montrent que le flux rotorique et le
couple suivent ses valeurs de consigne et ils présentent des
légers dépassements pendant le démarrage. =
0.55Wb. Les résultats montrent que le flux rotorique et le
couple suivent ses valeurs de consigne et ils présentent des
légers dépassements pendant le démarrage.
Figure 1.8 : Résultats
de simulation de test de découplage de l'orientation du flux
rotorique par la méthode indirecte.
1.3.3.3. Réglage de la MAS par la commande
vectorielle indirecte
Le schéma de principe de la commande en vitesse de la
machine asynchrone par la méthode indirecte est présenté
par la figure 1.9.
Figure 1.9 : Schéma de
principe de la commande vectorielle indirecte d'une MAS.
OND.
MLI
PARK-1
C
MAS
L
Redresseur
Filtre
Pont
PARK
IFOC
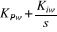
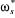
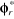
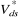
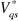
+
-
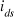
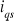
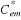
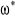
1.3.3.4. Résultat de simulation
Les paramètres du régulateur de vitesse sont
calculés par un emplacement de pôle ( ). ).
Pour évaluer les performances de la commande
vectorielle indirecte en vitesse, nous avons effectués des simulations
numériques sous les conditions suivantes (Figure 1.10) :
§ Démarrage à vide avec application d'un
échelon de vitesse de 100 rad/sec.
§ Application d'un couple de charge égale à
1 N.m à l'instant t = 1 sec, et puis la charge est
éliminée à l'instant t = 20 sec.
§ Inversion de sens de rotation à l'instant t = 30
sec.
La figure 1.10 montre que le réglage par un
régulateur PI donne des résultats satisfaisants :
§ La vitesse de rotation suit la vitesse de
référence ;
§ Le courant est bien limité à sa valeur
admissible ;
§ Le découplage est obtenu entre le flux rotorique
et le couple électromagnétique;
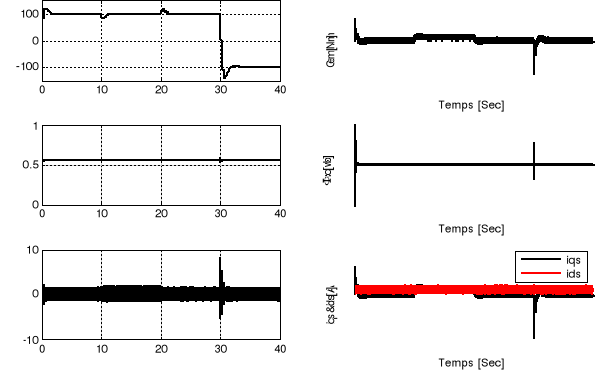
§ Les flux ( et et
 ) et le couple électromagnétique sont maintenus à
leurs valeurs désirées, impliquant ainsi un bon
découplage. ) et le couple électromagnétique sont maintenus à
leurs valeurs désirées, impliquant ainsi un bon
découplage.
Figure 1.10 : Réglage de
vitesse de la MAS par la commande vectorielle.
1.4. CONCLUSION
Dans ce chapitre, nous avons présenté un
modèle de la machine asynchrone sous forme de représentation
d'état. Le modèle non linéaire multivariable avec pour
entrées les tensions statoriques. Cette modélisation de la
machine asynchrone est donnée en considérant la structure du
système avec une partie primaire (le stator) et une partie secondaire en
court-circuit (le rotor). A partir d'un modèle triphasé, ce
modèle deux phases sont données dans le cadre de certaines
hypothèses permettant de simplifier la modélisation. Les
équations de flux, courants et tensions ont alors été
extraites. De plus, la modélisation est donnée en faisant
apparaître les variables d'états nécessaires aux objectifs
de commande. Cependant, pour se rapprocher de la réalité, il
serait naturel de prendre en considération les équations de
l'onduleur et de les faire intervenir dans la mise au point du modèle de
la machine.
La méthode d'orientation de flux rotorique qui a
été développée c'est la méthode
indirecte.
Cette méthode nous a permis de maintenir parfaitement
le découplage entre le couple et le flux, et rendre la machine
asynchrone similaire à une machine à courant continu, rendant
ainsi la commande de vitesse facile.
| 


