2.5 Résolvabilité des Systèmes
Mécanique Poly Articulés
2.5.1 Absence de solution :
2.5.1.1 Origine mécanique :
les mouvements du mécanisme tiennent compte des limites
des rotations et translations. Des butées empêchent le robot
d'atteindre les points en dehors de volume du travail malgré l'existence
de solutions mathématiques.
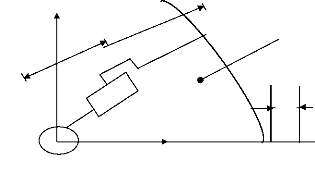
Surface de travail
Y
12
T
R0
a
Q0
X
Figure. 2.4 : Le robot R.P. [38]
Q
2-5-1-2 Origine mathématique :
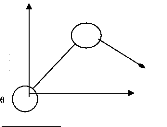
un système dont le nombre de variables est
inférieur au nombre d'équations ne donne pas de solutions
mathématiques. Cela revient, en robotique, à imposer plus de
contraintes qu'il n'existe de degrés de liberté.
Y
O2
1 Q X
Figure 2.5 : La structure R.P. [38]
1
R
0
2-5-2 Infinité de solution :
& f &
? j
×= j q
?? q j j
j
(2.10)
31
lorsque le nombre de contraintes est inférieur au
nombre de d.d.l .du robot, on se trouve en face de surabondance de
potentialités en fonction de la tâche demandée. La solution
consiste à réduire le nombre de variables articulaires en leur
imposant une valeur. Dans le second cas, le robot se trouve en position de
singularité.
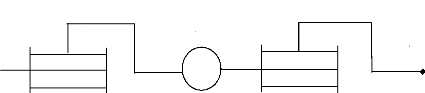
Cette configuration particulière est créée
par exemple lors de la mise en parallèle de deux axes.
è6
è4
è5
Q
Figure 2.6 : Représentation d'un
poignet. [38]
2-5-3 Nombre fini de solutions:
Si le nombre de contraintes est égal au nombre de d.d.l
.du mécanisme et si le robot ne se trouve pas dans un des cas
décrits plus haut, alors il existe une ou plusieurs solutions au
problème.
2-6 Calcul du modèle inverse :
Pour la résolution des problèmes inverse
c'est-à-dire résoudre le système d'équations non
linéaires, on utilisera les méthodes de Newton- Raphson,Range
kutta,loi de Bang-Bang et le formalisme de Newton-Euler (voir appendices).
2-7 Analyse cinématique : [4, 21,38,39 , 40, 71 ] :
*
Le modèle cinématique direct permet d'obtenir la
vitesse de l'organe terminal dans l'espace opérationnel en fonction des
vitesses articulaires.
En différenciant l'équation * on obtient:
La position de l'organe terminal dans l'espace
opérationnel peut être écrite en termes de variables
articulaires comme suit :
x = f(q)
[ & ×]=[J][ & q] (2.11)
?fj
[ ]
J
?q j
La Jacobinne du système est définie par :
(2.12)
Les accélérations sont données par :
|
& &
×
|
? ?
? ? ? ? ?
f & & & &
i q q
2 f i
+ +
q j j
j j
? q q q
j k j k
|
(2.13)
k
|
Ou bien sous forme matricielle par :
|
& &
x
|
= [ J ] & q & + [A] &
q2
|
(2.14)
|
|
ou : [ ]t
q q , q 2, ....
=
1
|
(2.15)
|
q & 2 = q & 1 q
& 1 , q & 1 q & 2 . .(2.16)
[ ]t
j (q) est la matrice Jacobienne donnée par :
? q
j q
( ) =
?fj
.(2.17)
f
Et : [ ] ??
A 2 .(2.18)
? ? ?
j = ??q q
? ? ?
j k ?
A partir du modèle cinématique (2.18) on peut
écrire le modèle différentielle (2.19). Supposons que les
variables qi soient maintenant non les variables articulaires de
DenavitHartenberg, mais les variables associées aux déplacements
des moteurs rotatifs ou linéaires et que le robot présente une
chaîne cinématique directe passant par ces moteurs. Il existe
alors un modèle différentiel du type (2.24). Chaque actionneur
peut associer en statique la force ou le couple ä i
qu'il exerce et forme le vecteur :
= [ä1 ä i ä
n ] T (2.19)
Des forces articulaires sous l'effet de ces forces
combinées, l'organe terminal exerce sur l'environnement des forces qui
peuvent être réduites à leur torseur résultant
(force et mouvement) noté F , qui a donc six composantes. En utilisant
alors la relation :
|
?P ?
N
? ? = 0 ( )
J q
? ù N?
|
q (2.20)
|
Ou: ( PN) : La vitesse du point de référence par
rapport au repère Fixe.
(ù N ) : La vitesse de rotation
instantanée et le principe des travaux virtuels pour des
déplacements infinitésimaux de type (2.24) ou à alors :
= 0 . (2.21)
J T f
Qui permet de calculer les forces matrices nécessaires
pour exercer sur l'environnement des forces données. L'équation
(2.22) constitue donc plutôt un modèle inverse au sens habituel du
terme. Le modèle direct ne peut s'obtenir que si la matrice J est
régulière.
Dans le cas d'un robot non redondant (n=6) et en dehors des
singularités, on a alors le modèle direct :
F J (2.22)
= ( ) -1
T
0
Tableau 2.1 : Les paramètres géométriques du
robot type.[140,141]
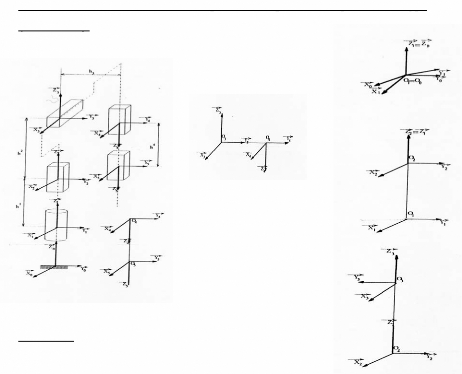
2-8 Détermination des matrices de changements de
repères <i-1/i> pour le robot type
(ALG-M.O. 1).
Figure 2.7 : Les différents repères
liés au corps du robot.
Indice
|
0
|
1
|
2
|
3
|
4
|
5
|
|
di
|
0
|
h1
|
h2
|
h3
|
h4
|
|
|
ái
|
|
0
|
ð/2
|
ð/2
|
0
|
|
|
ó
|
|
0
|
1
|
1
|
1
|
1
|
|
ri
|
|
0
|
Z 2
|
Z 3
|
Z 4
|
Z5
|
|
è i
|
|
ã
|
0
|
0
|
0
|
0
|
2-8-1 Espace de travail :
L'espace de travail est l'ensemble des positions et/ou
orientations accessible par l'organe terminal du robot.
Le volume ou l'espace de travail d'un robot dépend
généralement de trois facteurs : - De la géométrie
du robot,
- De la longueur des segments,
- Du débattement des articulations (limité par des
butées)
2-8-2 Analyse de l'espace de travail du robot type
(ALGERIE-MACHINES OUTILS-1) : L'analyse de l'espace de travail des robots
trouve de nombreuses applications. Notamment dans le domaine de la C.A.O.-
Robotique pour la conception optimale des robots, des sites robotisés,
et pour la programmation hors ligne.
Soit q = [q1 qn] un élément de
IRn représentant une configuration articulaire donnée
et
soit x = [x1 xn] l'élément de l'espace
opérationnel IRn correspondant, tel que :
X = f(q) (2.23)
On note Q l'ensemble des configurations accessibles compte tenu
des butées articulaires. Par conséquent, Q sera appelé
domaine articulaire :
L'image de Q par le modèle géométrique
direct f définit l'espace de travail W du robot :
W = f(Q) (2.24)
2-8-3 Calcul de l'espace de travail du robot choisi :
Comme on l'a définie précédemment, la
position de l'organe terminal dans le repère atelier est donnée
par le vecteur position dans la matrice de transformation qui exprime le
repère R5 dans R0 noté :

ã1
()
z z c
3 4
-
ã1
()
z z s
3 4
-
?
; avec ??
??
+ + + +
h h h z
2 3 4
ph= z 1
px
?
?
??
?
??
py
P
pz
?1
?
? ?
??
?
??
-
z5
2
px
py
(2.25)
En développant un programme qui a comme paramètres
entrées les limites articulaires de chaque articulation et sortie toutes
les configuration possibles de l'organe terminal.
2-8-4 Algorithme simplifié du programme :
Algorithme 2.1: Algorithme simplifié du programme
:
Début programme
Entrer h min et h max pour chaque
articulation ;
Début Do
Incrémentation de h1 et entre h1min
et h1max
Incrémentation de h2 et entre h2min
et h2max Incrémentation de h3 et entre h3min
et h3max
(
-
z3
)cã1
px
z4
ã1
() z z s
3 4
-
py
?
??
??
2 - z5
|
p h
=
z 1
|
+ + + +
h h h z
2 3 4
|
Fin Do
Sortie (Px,Py,Pz)
| 


