4.1.2 Analyse factorielle des correspondances (AFC)
L'analyse factorielle des correspondances (AFC) est une
technique statistique développée pour mettre en évidence
des correspondances entre des variables qualitatives décrivant une
population. L'AFC est également une méthode de réduction
de dimensionnalité qui facilite la représentation
géométrique des individus et des caractères.
Cette méthode a pour objectifs de :
- Représenter graphiquement et de manière optimale
des individus (lignes) en minimisant la déformation du nuage de
points,
- Représenter graphiquement les variables (colonnes) dans
un espace explici-
tant au mieux les liaisons initiales (corrélations) entre
ces variables,
- Réduire un système complexe de variables plus ou
moins corrélées en un plus petit nombre de dimensions.
L'AFC s'applique aux tableaux de contingence. Elle est
basée sur une métrique du Chi-2. Elle considère d'une
façon symétrique les lignes et les colonnes de la matrice. La
démarche de l'AFC est la suivante:
1. Transformation des données i.e. calcul du tableau XI
des pro...ls des lignes et du tableau XJ des pro...ls des colonnes,
2. Analyse en composantes principales des tableaux des
pro...ls,
3. Calcul des aides à l'interprétation: inertie
expliquée et contributions absolues et relatives.
Transformation des données
On considère un tableau Z de nombres positifs ou nuls,
comportant I lignes et J colonnes. On note nij son terme
générique, ni. et n.j les sommes
marginales, n la somme de tous les éléments du tableau:
J I I J
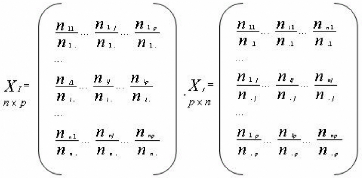
Les tableau des profils des lignes XI et des profils des colonnes
s'écrivent :
Analyse en composantes principales
L'AFC revient à appliquer l'ACP aux deux nuages N(I) et
N(J). Aux n lignes du tableau XI on associe le nuage N(I) et aux p lignes du
tableau XJ on associe le nuage N(J).
? ? n ? ?
N I I i n
( ) = , , 1, . . . ,
?? X i P
.
?? ?? ??
= ? R
?? ? n ? ??
..
? ? n ? ?
N J J j p
( ) = , , 1, . . . ,
n
?? ? X j
. ? ??
= ?
, R
?? ? n ?
..
? ? ??
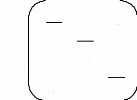
La distance choisie sur N(I) pour mesurer la proximité
entre deux points lignes est la distance du Â2 associée
à la métrique:
n..
1
n.
n..
n. j
n..
0
0
n.
p
MI = p ×p
Dans l'ACP du tableau XI, la matrice à diagonaliser est la
matrice CI avec
1 / 2 1 / 2
CI M I V I M I =
où VI est la matrice d'inertie du nuage N(I).
Dans l'ACP du tableau XJ, la matrice à diagonaliser est
la matrice CJ avec
1 / 2 1 / 2
C
J M J V J M J = où VJ est la matrice d'inertie du
nuage N(J).
4.1.3 Analyse factorielle des correspondances multiples
L'analyse factorielle des correspondances multiples (AFCM) est
une généralisation de l'AFC. Elle s'applique sur un tableau
disjonctif complet au lieu d'un tableau de contingence. Le tableau disjonctif
complet est construit à partir de descripteurs nominaux (qualitatifs) ou
continus mis en classes. Il consiste à »disjoncter» chaque
colonne descripteur en autant de colonnes que de modalités. Pour chaque
individu, l'occurrence d'une modalité est codée par 1, les autres
modalités étant codées par 0.
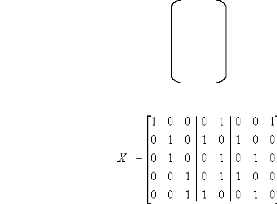
Soit le tableau suivant composé de 5 individus et 3
variables nominales :
123 211 222 321 312
Le tableau disjonctif complet :
Ses principes sont donc ceux de l'analyse des correspondances
à savoir:
- mêmes transformations du tableau de données en
profils-lignes et en profils- colonnes,
- même critère d'ajustement avec pondération
des points par leurs profils marginaux,
- même distance, celle du Â2.
L'AFCM présente cependant des propriétés
particulières dues à la nature même du tableau disjonctif
complet.
Les règles d'interprétation des résultats
(coordonnées, contributions, cosinus carrés) concernant les
éléments actifs d'une analyse des correspondances multiples sont
sensiblement les mêmes que celles d'une analyse des correspondances
simple.
| 


