Techniques d'extraction de connaissances appliquées aux données du Web

Chapitre 4

Méthodes de classification

Si dans les années 80, on distingue deux grands types de méthodes, les méthodes de partitionnement et les méthodes hiérarchiques, depuis d'autres approches (réseaux de neurones,...) ont vu le jour. Le choix de la méthode la plus adaptée dépend de la nature des variables, de la problématique posée et souvent des habitudes du domaine d'étude. Dans ce chapitre, nous présentons deux méthodes factorielles de classification, à savoir l'analyse en composantes principales et l'analyse des correspondances et une méthode connexioniste, les cartes topologiques de Kohonen.

4.1 Méthodes factorielles

L'objectif visé par l'analyse factorielle est la réduction de l'information en passant d'un grand nombre de variables, à un nombre restreint de méta-variables, appelés facteurs. L'essentiel de la démarche des méthodes factorielles est commun entre elles. Les »inputs» d'une analyse factorielle sont dans tous les cas l'espace, les points, les masses affectées aux points et la métrique. Les »outputs» sont les axes d'inertie, les coordonnées des points sur ces axes et divers indicateurs nommés »aides à l'interprétation». D'une méthode d'analyse factorielle à une autre, seuls varient les »inputs» i.e. les définitions des points, des masses et de la métrique [Jam, 99].

4.1.1 Analyse en composantes principales (ACP)

L'ACP est une méthode factorielle ayant pour but de déterminer un sous- espace vectoriel de dimension (k) inférieure à la dimension de l'espace d'entrée (k<p) et qui offre le maximum d'inertie expliquée pour y projeter le nuage de points de l'espace d'entrée R^p. En d'autres termes, réduire le nombre de variables à quelques facteurs significatifs et déterminer les relations de proximité entre

points individus et points variables. La démarche d'une ACP est présentée dans ce qui suit.

Calcul de la matrice d'inertie

Soit le tableau X (xij ; i=1..n; j=1. .p) formé de n points Xi munis de masses pi positives, décrits chacun par p variables:

	V1		Vj		Vp
X1
Xi	x1 i	..	xj i	..	xp i
Xn

La matrice d'inertie V s'écrit V=X'MX où X est la matrice à n lignes et p colonnes. Les lignes de X sont les vecteurs Xi, M est la matrice carrée diagonale d'ordre n des poids pi (généralement pi = 1/n).

V peut aussi s'écrire V=ZZ' avec Z= X'M¹=². Cette matrice a les propriétés suivantes :

- V est symétrique.

- V est diagonalisable et ses valeurs et vecteurs propres sont réels.

- Les vecteurs propres associés à des valeurs propres différentes sont orthogonaux.

- V est semi-définie positive et donc pour tout vecteur U de Rⁿ (espace d'entrée) on a U'VU positif. Toute valeur propre de V est donc supérieure ou égale à zéro.

- La trace de V, qui est la somme de toutes les valeurs propres, est égale à Tr(V)=P

i

i

Détermination des axes factoriels

Les axes engendrés par les vecteurs U1, . .Uk, vecteurs propres associés aux valeurs propres de V sont les axes principaux d'inertie. La k ième composante principale, ou le k ième facteur est le vecteur dont les composantes sont les coordonnées des points du nuage sur le k ième axe principal d'inertie Uk. Comme le nombre d'individus est n, ce vecteur a n composantes, c'est donc un élément de l'espace Rⁿ des variables.

Pour déterminer l'espace de projection à inertie expliquée maximale il faut déterminer ses k axes. Le premier est l'axe à inertie expliquée maximum. Pour

le déterminer, il suffit de chercher l'axe associé au premier vecteur propre de la matrice V. On désignera par U1le vecteur associé à la plus grande valeur propre 1. L'inertie expliquée par cet axe est égale à:

ë / ëi
1 ?i

Remarquons que l'inertie qui n'est pas expliquée par un sous-espace vectoriel donné l'est totalement par le sous-espace supplémentaire (ensemble des axes qui lui sont orthogonaux). Connaître le reste de l'inertie expliquée revient donc à déterminer les axes associés aux autres vecteurs propres.

Combien de facteurs faut-il retenir?

Retenir tous les facteurs équivaut à garder toute l'information initiale mais sans contribuer à la simplification de la structure des liaisons entres variables. Inversement, ne garder qu'un petit nombre de facteurs peut revenir à n'expliquer qu'un pourcentage trop faible de variance totale, et donc à résumer de façon excessive la complexité de la structure des liaisons entres variables, à moins que quelques facteurs seulement suffisent à expliquer une proportion importante de la variance totale. Généralement, la méthode adoptée est de garder les premiers axes factoriels dont la proportion expliquée de la variance atteint une proportion fixée, par exemple 80% (»critère» de »Jolie»). Il s'agit des premiers facteurs car leur pouvoir d'explication décroît du fait de leur ordonnancement par valeurs décroissantes de leur variance ®.

Représentation des individus

Les axes factoriels constituent une nouvelle base de l'espace Rp. Il est donc nécessaire de calculer les coordonnées des points sur ces axes pour les représenter dans la nouvelle base et plus précisément sur uniquement k axes.

La coordonnée ® d'un point Xi sur un axe U_® correspond à la projection du point sur l'axe, qui est aussi égal au produit scalaire entre Xi et le vecteur U_® de l'axe:

p

u_á i á ?= á

= =

'

( ) U X x u h

i ih

h 1

Pour interpréter les résultats d'une analyse en composantes principales nous avons aussi besoin de connaître:

- Pour chaque point Xi, la contribution du point à l'inertie du nuage. Cette contribution indique quels sont les points qui ont joué un rôle important dans l'analyse.

2

( )
i

CONTR i p i X i

( ) =

I o

( )

avec I(o) = Tr(V)

- Pour chaque axe U_® et chaque point Xi, la contribution du point à l'inertie expliquée par l'axe:

=

CTR_á

( )
i

p_i

u á

ë á

Les CTRs permettent d'interpréter un axe en identifiant les points qui ont le plus contribué à son positionnement. Notons que nous avons toujours :

n

?= =

CTR i

á ( )1

1

i

2

- Pour chaque point Xi et pour chaque axe U_®, on calcule la part de l'inertie du point restituée par l'axe et égale à:

2 ( )

u i

COS i á

( ) =

X_i

á 2

C'est en fait le carré du cosinus de l'angle formé par l'axe U_® et le point Xi.

COS i

2 =

á ( )1

p

?=

á 1

Représentation des points variables

Généralement, les variables utilisées dans l'ACP sont centrées. Le nuage des individus est donc centré. Son centre de gravité est situé à l'origine, ce qui n'est pas le cas pour le nuage des variables. Chaque variable Y correspond à une colonne du tableau X munie d'une masse unitaire. On utilisera comme représentation des variables la notation Z^® :

á 1 / 2 á 1 á

? ?

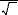
Z = M Y = n Y

? ?

? ?

car M est une matrice diagonale dont tous les termes sont égaux à 1/n. Toutes les variables Z sont normées et les points variables se situent à une

distance égale à 1 de l'origine. Elles sont donc sur la sphère de rayon 1. D'autre

part la distance entre deux variables est :

d²(Z^a,Z^fi )= Z^a --Z^fi2 = Za 2 #177; Z^{fi 2}--2 Z^a,Z^fi =2(1-- Z^a,Z^fi )

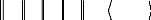
avec <Z^, , Z^E,> désigne le produit scalaire de deux variables.

Par ailleurs, le produit scalaire de deux vecteurs A et B est égal au produit des normes et du cosinus de l'angle entre les des deux vecteurs, donc

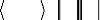
fi )

Z^a,Z^fi = _Za Zfi cos(Za,Zfi)=cosga,Z

car les variables sont normées. Ainsi,

)

d²(Z^a,Z^fi)=2(1--cosg^a,Z^fi

fi n

fi

Comme les variables sont centrées réduites, le coefficient de corrélation 1/2,E, est égal à

a

Z

=

1,z72 xi^axi t

=

afi

i=1 n i4

On peut donc dire que

)

pafi =COSga,Zfi

Les remarques suivantes seront utilisées pour donner un sens aux différents axes factoriels en fonction de la position des variables :

- Deux points variables confondus ont un coefficient de corrélation égal à 1.

- Deux points variables formant un angle de 90°ont un coefficient de corrélation linéaire égal à zéro.

- Deux points variables formant un angle de 180°ont un coefficient de corrélation linéaire égal à -1 (anti-corrélées).

- Pour comparer des points entre eux, il faut qu'ils soient proches de la circonférence du cercle de corrélation.

- Par contre, on ne peut rien dire quand les variables sont agglomérées au centre du cercle, ou de la sphère unité.

Aides à l'interprétation

L'ordre à suivre dans l'exploitation des indicateurs est le suivant :

1. Chercher les i correspondant aux CTR,(i) les plus forts. Sélectionner l'ensemble I' c I des points i tels que la somme des CTR, soit élevée (par exemple 0.8). L'interprétation de l'axe reposera sur l'examen de ces points.

2. Regarder le signe de 1,(i) pour i E I'. Ce signe indique si les points interviennent sur l'axe du côté positif ou du côté négatif.

. ?=

i ₁ n ij

n =

j

, ?

n j =

.

i=1

n ij , n n i 1

= =

.. .

? ? =

i=1 j

n. j

3. Examiner les COS² _®(i) pour i I^'. Si COS² _®(i) est fort, le point i est pratiquement aligné sur l'axe ®, il ne joue pas donc un grand rôle sur les autres axes. Inversement, si COS² _®(i) est faible, le point i joue un rôle important sur d'autres axes factoriels.