4.2 Cartes topologiques de Kohonen
Inspiré de l'auto-organisation des régions du
système nerveux1, Teuvo Kohonen [Koh, 95] introduit un type
particulier de réseau neuronal : les cartes topologiques (Self
Organizing Features Maps -SOFM), souvent appelées »cartes de
Kohonen», fondées sur l'apprentissage compétitif.
4.2.1 Architecture de la carte topologique
Une carte topologique est une grille composée
d'unités appelées neurones. Chaque neurone est lié aux
autres neurones suivant une topologie et connecté à toutes les
unités d'entrée dont le nombre correspond à la dimension
des données d'entrée. Comme les connexions sont
pondérées, chaque neurone peut être considéré
comme un vecteur de poids dont les composants représentent la force des
connexions synaptiques avec les données d'entrée. Le vecteur
d'entrée et les vecteurs de poids de tous les neurones ont les
mêmes dimensions.
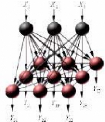
FIG. 4.1 : Architecture de la carte de Kohonen
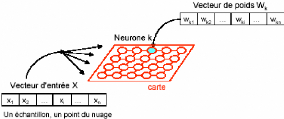
FIG. 4.2: Caractéristiques d'un neurone de la grille de
Kohonen
1Il a été observé que, dans de
nombreuses zones du cortex, des colonnes voisines ont tendance à
réagir à des entrées similaires. Dans les aires visuelles,
deux colonnes proches sont en correspondance avec deux cellules proches de la
rétine. Découvrant que ces propriétés au sein du
cerveau ne sont pas génétiques, mais dues à un
apprentissage, Kohonen a proposé un modèle de carte topologique
auto-adaptative.
4.2.2 Propriétés de la carte topologique
Quantification vectorielle
La carte de Kohonen a comme propriété de
réaliser une quantification vectorielle de l'espace des entrées
tout en respectant la distribution originale de ces entrées. En effet,
l'application de l'algorithme de Kohonen crée un ensemble, de taille
finie et fixée a priori, de prototypes, ou vecteurs codes, ayant les
mêmes dimensions que les données en entrée. Après
l'apprentissage, chacun de ces prototypes, reliés entre eux par une
relation de voisinage sur la carte, représente un sous-ensemble de
l'ensemble des entrées partageant certaines caractéristiques. A
la convergence, les neurones de la carte représentent des zones
formées autour de chacun des prototypes. Selon la terminologie de
Voronoï, ces prototypes sont considérés comme des
centroïdes des zones ou classes obtenues. Ces zones sont appelées
»cellules de Voronoï».
Réduction de la dimensionnalité
La réduction de la dimension de l'espace
d'entrée résulte de la combinaison de l'opération de
regroupement et de quantification citée précédemment, avec
la définition d'une structure de voisinage. Ainsi, en appliquant
l'algorithme SOM, l'espace d'entrée constitué par n individus
sera réduit en un espace de dimension inférieur (k<n)
constitué par un ensemble de micro-classes. Chaque classe est
représentée par la moyenne des caractéristiques des
individus qui la constituent.
Conservation de l'ordre topologique
La propriété de la conservation de la topologie
n'est pas vérifiée par d'autres méthodes de quantification
vectorielle. C'est une conséquence directe de l'équation de mise
à jour des vecteurs poids qui force le neurone gagnant et tous les
neurones appartenant à son voisinage topologique à se
déplacer vers le vecteur d'entrée. Ainsi, les entrées
ayant les mêmes caractéristiques sont projetées sur des
neurones voisins au niveau de la carte. Par conséquent, les
proximités des noeuds dans l'espace de sortie donnent une idée
sur la proximité des regroupements des individus dans l'espace
d'entrée.
| 


