A. Préparation des données :
1. Calcul des Temps de bon fonctionnement.
2. Classement des temps de bon fonctionnement en ordre
croissant.
3. Recherche des données F (i), F(i) représente
la probabilité de panne au temps correspondant au Temps de bon
fonctionnement de l'ième défaillant. On a 3 cas différents
:
§ Si N > 50, regroupement des Temps de bon
fonctionnement par classes avec la fréquence cumulée :
N ??(??) (2.12)
??(i) =
Ni
N =
? Ri
§ 29
Si 20 < N < 50, On affecte un rang "Ni" à chaque
défaillance (approximation des rangs Moyens)
Ni
??(i) = N+ 1
|
??(??) (2.13)
|
|
§ Si N < 20, On affecte un rang "Ni" à chaque
défaillance (approximation des rangs médians) :
|
??(i) =
|
Ni - 0.3
|
??(??) (2.14)
|
|
N+ 0.4
|
Et on fait le Tracé du nuage des points M (F(i), t)
B. Recherche de y :
Si le nuage de points correspond à une droite, alors gamma
= 0. (ã = 0)
Si le nuage de points ne correspond pas à une courbe,
on la redresse par une translation de tous les points en ajoutant ou en
retranchant aux abscisses "t", une même valeur (gamma) afin d'obtenir une
droite comme le montre la figure suivante.
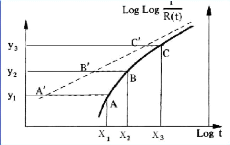
Figure 2-4: Redressement de la courbe par translation.
[1]
Ce redressement peut se faire par tâtonnement ou avec la
relation :
30
APPROCHE THÉORIQUE SUR LA MAINTENANCE ET LA
FMD
??3 * ??1 - ??2 2
?? = (2.15)
??3 + ??1 -
2??2
Considérons les points :
A (X1, Y1) ; B (X2, Y2) ; C (X3, Y3)
{
??3 > ??2 > ??1 2??2 =
??1 + ??3 En arrangeant on obtient :
(??3 - ??2). (??2
- ??1)
??= ??2 - (2.16)
(??3 - ??2) - (??2 -
??1)
C. Recherche de ti :
La droite de régression linéaire coupe l'axe A
à l'abscisse t = ç.
D. Recherche de f :
Bêta est la pente de la droite de corrélation. On
trace une droite parallèle à la droite de corrélation, et
passant par ç = 1 On lit ensuite bêta sur l'axe bêta est
sans dimension.
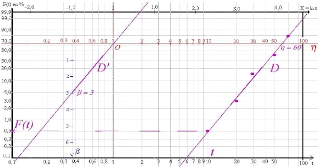
Figure 2-5: Recherche de bêta. [1]
2.2.2.1.5. Test de KOLMOGOROV SMIRNOV (K-S)
Avant la validation de toutes les Lois de fiabilité, il
est nécessaire de tester l'hypothèse pour savoir si nous devrons
accepter ou rejeter le modèle proposé par le test de K-S avec un
seuil de confiance de = 20%. Ce test consiste à calculer l'écart
entre la fonction théorique Fe(ti) et la fonction réelle F(t)
et prendre le maximum en valeur absolue Dn.max.
Cette valeur est comparée avec Dn. Qui est
donnée par la table de Kolmogorov Smirnov (voir annexe1). Si Dn.max.
> Dn. On refuse l'hypothèse.[1]
APPROCHE THÉORIQUE SUR LA MAINTENANCE ET LA
FMD
2.2.2.1.6. La fiabilité d'un
système
La détermination de la fiabilité d'un
système électronique, mécanique ou autre nécessite
tout d'abord de connaître la loi de la fiabilité (ou la loi de
défaillance) de chacun des composants intervenant dans le
système.
2.2.2.1.7. La fiabilité des systèmes
constitués de plusieurs composants A. En série
La fiabilité Rs d'un ensemble de n
constituants connectés en série est égale au produit
des fiabilités respectives RA, RB, RC... Rn de chaque
composant.
R??= R??.R??.R??....R?? (2.17)
Si les «n» composants sont
identiques avec une même fiabilité R la formule
sera la suivante :
R?? = R ?? (2.18)

31
Figure 2-6: Composants en série.
Si les taux de défaillances sont constants au cours du
temps, la fiabilité sera calculée suivant la formule :
R?? = (??-??????). (??-??????). (??-??????) ... (??-??????)
(2.19)
Avec :
1
??????F?? = A??+ A??+ A??...A?? (2.20)
Si en plus, les composants sont identiques : A?? = A?? = A??
= ? = A??
Alors :
??(??) = (??-??????) (2.21)
|
??????F?? =
|
1 (2.22)
??* A
|
| 


