2.2. Test de cointégration aux bornes
Nous avons signalé que le test de cointégration
de Pesaran et al. (2001) était adapté pour les types de
séries comme les nôtres. Aussi, rappelons qu'il y deux
étapes à suivre pour appliquer le test de cointégration de
Pesaran, à savoir :
Ø Détermination de décalage optimal avant
tout suivant les critères d'information (AIC, SIC) et
Ø Recourir au test de Fisher pour tester la
cointégration entre séries.
2.2.1. Décalage optimal et
estimation du modèle ARDL
Nous allons ici nous servir du critère d'information de
Schwarz (SIC) pour sélectionner le modèle ARDL optimal, celui qui
offre des résultats statistiquement significatifs avec les moins des
paramètres. Les résultats d'estimation du modèle ARDL
optimal retenu est :
Tableau 5: Résultats de l'estimation du
modèle ARDL (1, 3, 0, 0, 1, 0)
|
Variables
|
Coefficients
|
Ecart-Type
|
t-Statistic
|
Prob
|
|
LCE (-1)
|
0.432529
|
0.082412
|
5.248392
|
0.0000
|
|
LCP
|
-0.016664
|
0.016993
|
-0.980628
|
0.3290
|
|
LCP (-1)
|
0.016707
|
0.017590
|
0.949829
|
0.3444
|
|
LCP (-2)
|
0.012794
|
0.017453
|
0.733064
|
0.4651
|
|
LCP (-3)
|
-0.072116
|
0.017312
|
-4.165656
|
0.0001
|
|
LPE
|
0.151941
|
0.395805
|
0.383878
|
0.7018
|
|
LPP
|
0.247243
|
0.264233
|
0.935701
|
0.3516
|
|
LDFC
|
-0.000785
|
0.008107
|
-0.096835
|
0.9230
|
|
LDFC (-1)
|
-0.014557
|
0.008048
|
-1.808632
|
0.0733
|
|
LIPC
|
-0.003438
|
0.061340
|
-0.056049
|
0.9554
|
|
C
|
3.306280
|
1.318588
|
2.507440
|
0.0137
|
|
R-squared
|
0.580395
|
Durbin-Watson stat
|
2.175623
|
|
Adjusted R-squared
|
0.540809
|
|
F-statistic
|
14.66184
|
|
Prob(F-statistic)
|
0.000000
|
Source : nous-mêmes sur base des
résultats tirés (annexe 5)
Graphique 5 : Valeurs graphiques du modèle
ARDL
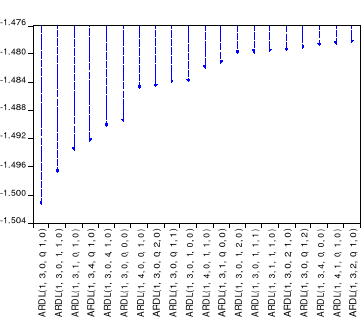
Comme on peut le voir sur le graphiques ci-dessus des valeurs du
modèle ARDL (1, 3, 0, 0,1, 0) est le plus optimal parmi les 19 autres
modèles présentés, car il offre la plus petite valeur du
SIC. Par ailleurs, au regard des tests qui aident à diagnostiquer le
modèle ARDL estimé, l'on note l'absence d'autocorrélation
des erreurs, il n'y a pas d'hétéroscédasticité, les
erreurs n'est pas bruit blanc et le modèle a été bien
spécifié voir le tableau ci-dessous :
Tableau 6 : Résultats des tests
diagnostiques du modèle ARDL estimé
|
Hypothèse du test
|
Tests
|
Valeurs
|
Probabilité
|
|
Autocorrélation
|
Breusch-Godfrey
|
1,445
|
0,240
|
|
Hétéroscédasticité
|
Arch-Test
|
1,978
|
0,162
|
|
Breusch-Pagan-Godfrey
|
1,713
|
0,134
|
|
Normalité
|
Jarque-Bera
|
13,578
|
0,001
|
|
Spécification
|
Ramsey (Fisher)
|
1,881
|
0,063
|
Source : nous-mêmes sur base des
résultats tirés (annexe 7)
L'hypothèse nulle est acceptée pour tous ces
tests sauf pour le test de normalité des résidus mais cela
n'empêche pas de valider notre modèle sur le plan statistique. Le
modèle ARDL (1, 3, 0, 0, 1, 0) estimé est globalement bon et
explique à 58 la dynamique de la consommation de l'essence en RD Congo,
de janvier 2010 à décembre 2019.
| 


