2. Analyse et traitement des
données
Pour ce qui est de l'analyse et traitement des données,
nous allons à travers le logiciel économétrique le plus
couramment utilisé dans le domaine économique et de gestion, le
logiciel EViews 10. Ce logiciel est beaucoup plus adapté pour les
analyses économétriques, et la version que nous disposons nous
offre les possibilités de faire toutes les tests qui seront
énumérées. Pour ce faire, l'on notera ici qu'avant de se
soumettre à une quelconque estimation, nous allons étudier divers
tests préliminaires à l'estimation du modèle
économétrique, à savoir : test de
stationnarité des séries particulièrement à travers
le test statistique (Dickey et Fuller Augmented 1981), suivie du test de
causalité (Granger) pour examiner les effets de feedback et de
l'estimation du modèle.
2.1. Test de stationnarité : Test de racine
unitaire Dickey et Fuller
La stationnarité est un concept clé de toute
analyse de séries temporelles ou chronologiques ; de ce fait, avant
la mise en oeuvre de notre modèle, il est primordial de vérifier
la stationnarité des séries d'étude. Comme annoncé
ci-haut, nous allons faire recours au test le plus couramment utilisé,
il sera donc question du test ADF. En effet, ce test quant à lui sert
à vérifier à nouveau la stationnarité de nos
séries avec comme particularité la faite de se baser sur le
caractère de la racine unitaire. Il repose sur deux hypothèses,
à savoir :
- H0 : la série contienne des racines
unitaires, donc non stationnaire ;
- H1 : la série n'a pas des racines unitaires,
donc stationnaire.
Partant de ces hypothèses, deux conditions sont
à vérifier, il s'agit :
Si la valeur absolue de t-Statistique d'ADF dans l'un des
trois modèles (Intercept and trend, Intercept et None) est
supérieure aux valeurs absolues de ses valeurs criques dans les trois
degrés 1%, 5% et 10%, on rejette H0 et on accepte H1.
En revanche, dans le cas contraire, on rejette H1 et on
accepte H0. Cette procédure étant presque la même,
lorsqu'on décide de procéder à la vérification de
ces hypothèses, en faisant plus référence aux valeurs de
probabilité qu'il faudrait comparés au seuil de
significativité qui est de 5%. De ce fait, si la valeur de la
probabilité critique est inférieure à 0,05 on accepte H1
et on rejette H0. Dans le cas contraire, on accepte H0 et on rejette H1.
Tableau 4 : Résultats synthétiques
du test ADF
|
Variables
|
Au Niveau
|
En différence
|
Conclusion
|
|
ADF à 5%
|
t-Stat
|
Prob
|
t-Stat
|
Prob
|
|
LCE
|
-3,789
|
-2,886
|
0,004
|
-
|
-
|
I(0)
|
|
LCP
|
-1,151
|
-1,944
|
0,226
|
-10,671
|
0,000
|
I(1)
|
|
LPE
|
1,013
|
-1,943
|
0,917
|
10,541
|
0,000
|
I(1)
|
|
LPP
|
-,2226
|
-2,886
|
0,198
|
-10,367
|
0,000
|
I(1)
|
|
LDFC
|
-7,102
|
-2,886
|
0,000
|
-
|
-
|
I(0)
|
|
LIPC
|
-2,773
|
-3,450
|
0.210
|
-4,669
|
0,001
|
I(1)
|
Source : nous-mêmes sur base des résultats
tirés (annexe 4)
Les résultats de ce tableau montrent que quatre de six
variables sont stationnaires après la différence première
et deux autres sont stationnaires en niveau. Les variables stationnaires en
différence première se présentent comme suit après
avoir appliqué le filtre en différence première :
Graphique 4 : Variables stationnaire en
différence première
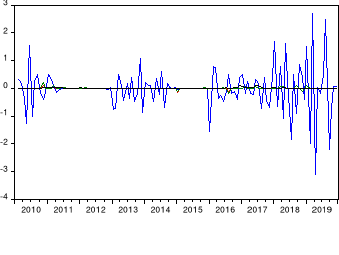
Source : nous-mêmes sur base des résultats
tirés sur EViews 10
Les séries sont ainsi intégrées à
des ordres différents, ce qui rend inefficace le test de
cointégration et ne valide pas la spécification VAR et
l'estimation du modèle vectoriel à correction d'erreur
développé par Johansen (1988, 1991) et rend opportun le test de
cointégration aux bornes (Pesaran, 2001). Le modèle de Johansen
été conçu pour des cas multivariés constitué
un remède aux limites du test de Engle et Granger pour le cas
univarié, il exige aussi que toutes les séries ou variables
soient intégrées de même ordre ce qui n'est pas toujours le
cas en pratique, comme c'est le cas pour ce qui nous concerne. Cependant,
lorsqu'on dispose de plusieurs variables intégrées d'ordres
différents (I (0), I (1)), l'on peut recourir au test de
cointégration de Pesaran et al. (2001) appelé « test de
cointégration aux bornes ». Si l'on recourt au test de
cointégration de Pesaran pour vérifier l'existence d'une ou
plusieurs relations de cointégration entre les variables dans un
modèle ARDL, l'on dira que l'on recourt à l'approche
« ARDL approach to cointegrating » ou que l'on applique le
test de cointégration par les retards échelonnés (Jonas
Kibala, 2009).
A cet effet, l'objectif de ce chapitre comme décrit
ci-haut est de saisir les effets sur la consommation des produits
pétroliers à l'occurrence l'essence (lce : variable
dépendante) de la consommation du pétrole, du prix de l'essence,
du prix du pétrole et de la dépréciation du franc
congolais (lcp, lpe, lpp et ldfc :
variables d'intérêt), tenant compte de la variable de
contrôle indispensable dont l'influence améliore les effets, il
s'agira : l'indice des prix à la consommation ipc. Ainsi,
nous nous proposons d'estimer un modèle ARDL suivant la nature de nos
variables et l'ordre d'intégration qu'affiche chacune de variable pour
la fonction suivante (forme fonctionnelle linéaire) :
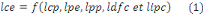
Si l'on se propose de saisir les effets de court terme et ceux
de long terme des variables explicatives ci-dessus sur la consommation de
l'essence, la représentation ARDL de la fonction suivante (1)
sera :
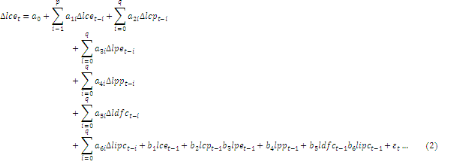
Avec   : opérateur de différence première ; : opérateur de différence première ; 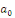 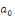 : constante ; : constante ; 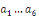 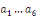 : effets à court terme ; : effets à court terme ; 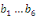 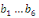 : dynamique de long terme du modèle ; : dynamique de long terme du modèle ; 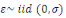 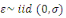 : terme d'erreur (bruit blanc). : terme d'erreur (bruit blanc).
Comme pour tout modèle dynamique, nous nous servirons
des critères d'information (Schwarz-SIC) pour déterminer les
décalages optimaux (p, q) du modèle ARDL, par parcimonie.
| 


