3.3 Outils de modélisation
Définition 3.3.1. La
modélisation mathématique consiste à utiliser des outils
mathématiques tels que des équations, des fonctions, des graphes,
des systèmes dynamiques ou des algorithmes pour représenter et
étudier des situations réelles ou abstraites. La
modélisation permet de simplifier et de formaliser un système
complexe en le décrivant de manière précise et
quantitative, ce qui permet d'en comprendre les propriétés et de
prédire son comportement dans différentes conditions.
la résolution de problèmes de l'optimisation
combinatoire est souvent difficile et nécessite des outils de
modélisation mathématique pour formaliser les problèmes et
les transformer en modèles mathématiques.Les outils les plus
souvent requis pour l'optimisation combinatoire sont:
3.3 Outils de modélisation 25
3.3.1 La théorie des graphes
La théorie des graphes fournit des outils pour
résoudre les problèmes d'optimisation combinatoire. Elle offre
des algorithmes pour trouver des chemins optimaux, des couplages ou des flots
maximaux. Les résultats obtenus peuvent permettre de prendre des
décisions plus éclairées et d'optimiser les ressources
disponibles pour atteindre des objectifs spécifiques. La théorie
des graphes est donc une approche importante pour résoudre les
problèmes d'optimisation combinatoire.
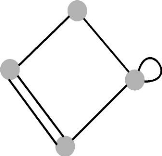
Un exemple d'un graphe simple est représenté
ci-dessous:
e5
e3
2
e1 e
2
e 6
1 3
e4
4
G = (V, E) où :
V = {1, 2,3, 4} est
l'ensemble des sommets de graphe G
E = {e1, e2, e3, e4, e5, e6} est l'ensemble
des arêtes de graphe G
-Page 25-
FIGURE 3.1 - Graphe simple -G-
3.3.2 La programmation linéaire (PL)
Le principe de la programmation linéaire est de
modéliser le problème sous forme de contraintes
mathématiques linéaires, c'est-à-dire sous forme
d'équations ou d'inéquations linéaires reliant les
variables du problème. La fonction objectif, qui est à maximiser
ou à minimiser, est également une fonction linéaire.
?
?????
?????
(PL)
La forme générale d'un programme linéaire
est la suivante:
maximiser z = cx
sous contraintes: Ax = b
x = 0
Avec A E m×n
est une matrice (m x n),où
rang(A) = m < n, b E m
un vecteur de
3.3 Outils de modélisation 26
-Page 26-
dimension m, c E Rn un vecteur de dimension n et x E
Rn est un vecteur inconnu.
Remarque 3.3.1. Tout programme
linéaire peut s'exprimer sous forme standard en ajoutant certaines
variables appelées variables d'écart, (par exemple, une
inéquation a.x1 < b devient l'équation a.x1 + x2
= b, x2 > 0).
| 


