Chapitre 5 CHAPITRE 3 : ANALYSE DE L'EFFET
DE LA DIVERSIFICATION DES EXPORTATIONS SUR LA CROISSANCE ECONOMIQUE
Dans cette partie,il s'agit principalement de mesurer l'effet
de la diversification des exportations sur la croissance économique. La
méthodologie que nous adoptons joue un rôle fondamental dans
l'attente de notre objectif de recherche, car elle détermine la
manière dont nous collectons, analysons et interprétons les
données nécessaires pour répondre à notre question
de recherche. En d'autres termes, c'est à travers la méthodologie
que nous nous efforçons d'atteindre une compréhension approfondie
et rigoureuse du sujet étudié. Le modèle de croissance
linéaire développé par Mankiw et al (1992) sera
adopté.Nous utiliserons comme modèle d'estimation, la
méthode des moindres carrés ordinaires (MCO).
SECTION 1 :METHODOLOGIE DE LA RECHERCHE
Cette section met en évidence successivement la
présentation du modèle théorique, la source des
données, la liste des variables retenues, leurs descriptions et signes
attendus et la spécification du modèle empirique.
1.1 Présentation du
modèle théorique
Nous nous basons dans notre étude, sur le modèle
de croissance de Mankiw et al. (1992), Knight et al. (1993), Ghra et
Hadjmichael (1996) et Demetriades et Law (2006).
Notre point de départ est la fonction de production de
type CobbDouglass suivante :
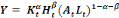 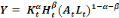 (1) (1)
Avec :
- Y, le Produit Intérieur Brut
réel par tête ;
- K, le stock de capital physique ;
- H, le stock de capital humain ;
- L, le travail brut ;
- A, facteur reflétant le niveau de
technologie et d'efficacité dans une économie donnée ;
- t, la période.
On suppose que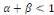 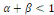 , c'est-à-dire que la recette est supposée
décroissante pour tout le capital (capital physique et capital humain).
Le travail brut (L) et le niveau de technologie (A) sont donnés par les
fonctions suivantes : , c'est-à-dire que la recette est supposée
décroissante pour tout le capital (capital physique et capital humain).
Le travail brut (L) et le niveau de technologie (A) sont donnés par les
fonctions suivantes :
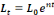 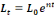 (2) (2)
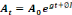 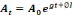 (3) (3)
Avec :
- n, le taux de croissance exogène du
travail ;
- g, le taux de croissance exogène du
progrès technologique ;
- I, un vecteur des variables
institutionnelles qui peuvent affecter le niveau de technologie et d'efficience
dans une économie donnée ;
 - -  , un vecteur des coefficients reliant ces variables institutionnelles. , un vecteur des coefficients reliant ces variables institutionnelles.
Dans ce modèle, la variable A dépend des
améliorations technologiques exogènes, du degré
d'ouverture commerciale et du niveau des autres variables. Il est
évident que la variable A, dans notre étude, diffère de
celle employée par Mankiw et al (1992). A l'état
d'équilibre, le rendement par ouvrier augmente à un taux constant
g (la composante exogène du taux de croissance de la variable
reflétant le niveau de technologie et d'efficience d'une
économie). Ces résultats peuvent être obtenus directement
à partir de la définition du rendement par ouvrier efficace
(productivité moyenne du travail) :
À partir des équations
précédentes, on obtient en log linéarisant
l'équation (4) suivante :
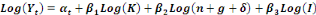 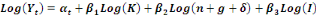 (4) (4)
Avec :
- Y, le Produit Intérieur Brut par
ouvrier (PIB/tête) ;
- I, un vecteur regroupant les variables
institutionnelles ;
- K, le stock du capital en investissement ou
accumulation du capital physique ;
- n, taux de croissance du travail (force de
travail) ;
- g, taux de croissance de la technologie ou
du progrès technologique ;
- ä, taux de dépréciation
du capital.
| 


