2.1.2. Estimation du modèle VECM
En effet, l'estimation du modèle VECM permet de
déterminer le vecteur de la cointégration â. Pour ce faire,
nous nous appuyons sur les procédures d'estimation fournies par le
package «vars» du logiciel R. Ainsi, l'équation de
cointégration nous offre une forme d'équilibre de long terme,
laquelle est obtenue à partir de l'équation de
cointégration suivante (Annexe6) :
åt-1 = NPLt-1 + 2.41ROAt-1 -
7.42????????-1 + 160.74IPCt-1 -
368.55IPIt-1 - 5.33TMMt-1 -
88.61USDt-1
En se basant sur ces résultats d'estimation, nous
pouvons dériver l'équation du modèle VECM comme suit :
NPLt = -17.838 + 0.665 NPLt-1 + 0.059
ROAt-1 + 0.443 ????????-1 - 3.509 IPCt-1 - 5.066 IPIt-1
+ 0.406 TMMt-1 - 2.239 USDt-1 + 0.071 NPLt-2 -
0.230ROAt-2 + 0.363 ????????-2 - 4.832 IPCt-2 - 2.758
IPIt-2 + 0.165 ????????-2 - 1.974 USDt-2 +
åt
Les résultats de validation du modèle VECM
montrent, selon l'annexe 7, que les résidus sont stationnaires, non
corrélés et suivent la loi normale d'après les tests ADF,
Breusch-Godfrey et Jarque Bera respectivement. Enfin, les résultats du
test d'hétéroscédasticité montrent que la
probabilité associée est supérieure à 5%, ce qui
signifie l'existence d'Homoscédasticité des résidus.
(Annexe7)
2.2.Application de l'approche BSVAR
Dans le cadre de notre objectif d'étude, nous
introduirons, dans cette partie, l'approche de la statistique structurelle et
bayésienne en utilisant les mêmes variables que celles
employées dans le modèle VECM.
Dans la méthode scientifique, il existe deux types de
probabilités différents, ce qui peut créer de la confusion
parmi les chercheurs. Ce sont fondamentalement deux façons de penser
distinctes, qui visent à élaborer des opinions sur le
fonctionnement de la nature et la composition de la réalité.
La principale différence entre les deux approches
réside dans le fait que l'approche fréquentiste raisonne en
termes de vraisemblance, tandis que l'approche bayésienne raisonne en
termes de
54
plausibilité (ou crédibilité) des
hypothèses. La raison qui explique ce choix par les fréquentistes
est qu'ils estiment que l'approche bayésienne comporte deux critiques
majeures :
- Trop complexe : Ce n'est pas le cas lorsque
des logiciels et des algorithmes sophistiqués tels que le logiciel
R-CRAN sont disponibles. Pour remédier à ce problème, les
fréquentistes raisonnent en termes de vraisemblance à travers la
statistique de Fisher, qui se base sur des intervalles de confiance
fixés par les chercheurs, pouvant aller jusqu'à 10 % pour
accepter une hypothèse. Cela pose un problème majeur, en
particulier dans les cas de crises et de stress. En revanche, l'approche
bayésienne fonctionne par inférence, ce qui signifie qu'il n'y a
pas de rejet des hypothèses, mais au fil de nombreuses
itérations, on s'approche de la réalité, avec la
possibilité de prendre en compte toutes les hypothèses existantes
et/ou d'intégrer de nouvelles hypothèses.
- Trop subjectif : Cette objection ne tient
pas non plus, car la statistique fréquentiste utilise également
une forme de subjectivité, en particulier à travers le principe
de parcimonie, souvent appelé « le Rasoir d'Ockham ».
Figure 3 : Différences entre les approches
fréquentiste et bayésienne
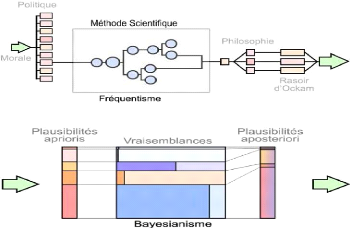
Source : Livre formule du savoir Lê Nguyên
2018
D'après (Nguyên, 2018), la statistique
bayésienne est une méthode globale qui a une grande portée
philosophique et qui contribue significativement à une réflexion
approfondie. Elle répond de manière adaptée au contexte
des tests de stress en évaluant la plausibilité des
hypothèses et en intégrant une dimension critique pour les
décideurs.
55
Cependant, avant de pouvoir procéder à ce
traitement, il est nécessaire de spécifier des contraintes
d'identification. Dans notre cas, avec un modèle à sept
variables, nous sommes amenés à introduire 21 contraintes
d'identification, conformément à la règle (??(?? -
1)/2).
Par conséquent, en s'inspirant, principalement, des
travaux de (Sims & Zha, 1998) et de (Waggoner & Zha, 2003), on
définira le cadre de notre modèle BSVAR, surtout concernant la
nature et les spécificités de la distribution à priori.
| 


