5.3.1 Calcul de pondération des critères
Les critères sont de différentes
catégories : certains sont qualitatifs et d'autres quantitatifs.
Cependant, par la pondération, il est possible de les comparer en
commençant par l'étape de la décomposition
hiérarchique.
5.3.1.1 Hiérarchisation des critères
La hiérarchisation entre les différentes
alternatives est une étape importante pour comprendre comment chaque
critère apporte sa contribution dans l'atteinte de l'objectif principal
ou cible.
43
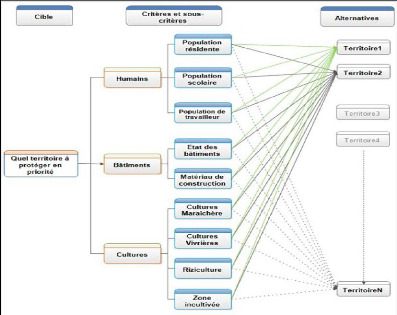
Figure 5.3: Structure explicative du système de
critères à comparer
D'abord, le schéma illustre le jeu d'influence des
critères et des sous-critères sur le degré de
vulnérabilité des alternatifs. Après la connaissance de la
vulnérabilité, il est aisé de connaitre les portions de
territoire les plus fragiles à protéger en toute
priorité.
5.3.1.2 Comparaison des critères
En effet, les critères sont comparés entre eux
suivant leurs niveaux hiérarchiques décrits dans la figure 5.3
précédente. La comparaison se fait deux à deux entre les
enjeux ainsi que deux à deux entre les propriétés de
chaque enjeu.
5.3.1.2.1 Comparaison entre les enjeux
La protection des personnes est l'élément le
plus important à considérer lors de la réalisation des
aléas et surtout des inondations. En plus, la présence des
personnes explique la plupart des enjeux présents dans une zone.
Ainsi, par cette comparaison, il est défini que la vie
humaine est très importante par rapport aux cultures et entre
modérément et fortement plus importante par rapport aux
44
bâtiments. De même, les bâtiments sont
modérément plus importants que les cultures car les
bâtiments abritent des vies humaines.
Tableau 5.1 : Matrice de calcul entre les
enjeux
|
Cultures
|
Bâtiments
|
Humains
|
Wi
|
Ti
|
|
Cultures
|
1,00
|
0,33
|
0,14
|
0,36
|
0,09
|
|
Bâtiments
|
3,00
|
1,00
|
0,25
|
0,91
|
0,21
|
|
Humains
|
7,00
|
4,00
|
1,00
|
3,04
|
0,70
|
|
Total
|
|
|
|
4,31
|
1,00
|
X=0.032 ; IC=0.016 ; RC=0,028
5.3.1.2.2 Comparaison entre les
propriétés des enjeux humains
La population résidente est très importante
comparant à la population scolaire et fortement plus importante que la
population de travailleur. Car, lors d'annonce d'averses importantes, il y a de
fortes possibilités que les travailleurs et les élèves
sont restés chez eux. En effet, au regard des horaires de travail et de
fonctionnement des écoles, la population résidente s'expose face
à cet aléa le plus longtemps que les autres types de population.
La population scolaire est modérément plus importante que la
population de travailleur vu la fragilité des enfants en
général.
Tableau 5.2 : Matrice de calcul entre les
propriétés des enjeux humains
|
Travailleur
|
Scolaire
|
Résidente
|
Wi
|
Ti
|
|
Travailleur
|
1,00
|
0,33
|
0,14
|
0,36
|
0,08
|
|
Scolaire
|
3,00
|
1,00
|
0,20
|
0,84
|
0,19
|
|
Résidente
|
7,00
|
5,00
|
1,00
|
3,27
|
0,73
|
|
Total
|
|
|
|
4,48
|
1,00
|
X=0.065 ; IC=0.032 ; RC=0,056
5.3.1.2.3 Comparaison entre les
propriétés des enjeux des bâtiments
Les matériaux de construction sont d'abord plus
importants à prendre en considération par rapport à
l'état des maisons. Puisque suivant les matériaux de
construction, les dégâts peuvent être plus marqués.
Le tuf est friable et se détériore facilement avec action de
l'eau de pluie qui est légèrement acide. Ce qui s'explique par la
solubilité du CaCO3 lors de la submersion. (CORTIAL, 2008)
45
Tableau 5.3 : Matrice de calcul entre l'état et
les matériaux des bâtiments
|
Etat
|
Matériau
|
Wi
|
Ti
|
|
Etat
|
1,00
|
0,20
|
0,45
|
0,17
|
|
Matériau
|
5,00
|
1,00
|
2,24
|
0,83
|
|
Total
|
|
|
2,68
|
1,00
|
Tableau 5.4: Matrice de calcul entre les deux types de
matériaux (bloc et tuf)
|
Bloc
|
Tuf
|
Wi
|
Ti
|
|
Bloc
|
1,00
|
0,50
|
0,71
|
0,33
|
|
Tuf
|
2,00
|
1,00
|
1,41
|
0,67
|
|
Total
|
|
|
2,12
|
1,00
|
Tableau 5.5 : Matrice de calcul entre les états
des bâtiments
|
Bon
|
Moyen
|
Mauvais
|
Wi
|
Ti
|
|
Bon
|
1,00
|
0,25
|
0,11
|
0,30
|
0,06
|
|
Moyen
|
4,00
|
1,00
|
0,25
|
1,00
|
0,22
|
|
Mauvais
|
9,00
|
4,00
|
1,00
|
3,30
|
0,72
|
|
Total
|
|
|
|
4,60
|
1,00
|
X=0.037 ; IC=0.018 ; RC=0,032
5.3.1.2.4 Comparaison entre les propriétés
des enjeux des cultures
Les pertes pour les cultures maraîchères seront
plus importantes lors des inondations puisque ces plantes ont des tissus
végétatifs plus sensibles et plus fragiles par rapport à
la submersion. Toutefois le riz est une culture inondée qui donne
généralement de meilleur rendement dans les zones
inondées. Les autres cultures vivrières sont relativement
sensibles par rapport à la durée de la submersion.
Tableau 5.6 : Matrice de calcul pour les enjeux
culturaux
|
Non-cultivée
|
Riz
|
Vivrière
|
Maraîchère
|
Wi
|
Ti
|
|
Non-cultivée
|
1,00
|
0,33
|
0,14
|
0,13
|
0,28
|
0,04
|
|
Riz
|
3,00
|
1,00
|
0,17
|
0,14
|
0,52
|
0,08
|
|
Vivrière
|
7,00
|
6,00
|
1,00
|
0,33
|
1,93
|
0,31
|
|
Maraîchère
|
8,00
|
7,00
|
3,00
|
1,00
|
3,60
|
0,57
|
|
Total
|
|
|
|
|
6,33
|
1,00
|
X=4.232 ; IC=0.077 ; RC=0,086
46
5.3.1.2.5 Comparaison entre les mailles
Les mailles sont comparées en fonction des
densités de la population résidente, de la population scolaire,
de la population de travailleur, de bâtiment en tuf, de bâtiment en
bloc, de bâtiments en bon état, de bâtiments en moyen
état, de bâtiments en mauvais état. Pour les cultures, les
différences entre les mailles ne sont portées que sur la nature
des cultures. Dans une maille, il n'est rencontré qu'un type de culture
parmi ceux définis.
Tableau 5.7: Calcul de matrice pour la population
résidente
|
Classe-
densité
|
Milieu-
classe
|
0
|
6
|
25,5
|
59
|
107
|
Wi
|
Ti
|
|
[0-0]
|
0
|
1,00
|
0,69
|
0,34
|
0,18
|
0,11
|
0,34
|
0,042
|
|
[0-12]
|
6
|
1,45
|
1,00
|
0,41
|
0,20
|
0,12
|
0,43
|
0,052
|
|
[12-39]
|
25,5
|
2,91
|
2,46
|
1,00
|
0,29
|
0,14
|
0,78
|
0,095
|
|
[39-79]
|
59
|
5,41
|
4,96
|
3,50
|
1,00
|
0,22
|
1,83
|
0,224
|
|
[79-135]
|
107
|
9,00
|
8,55
|
7,09
|
4,59
|
1,00
|
4,78
|
0,586
|
|
Total
|
|
|
|
|
|
|
8,16
|
1,000
|
X=5.194 ; IC=0.049 ; RC=0,043
Tableau 5.8: Calcul de matrice pour la population
scolaire
|
Classe-
densité
|
Milieu_ classe
|
0
|
17
|
143,5
|
346,5
|
614,5
|
Wi
|
Ti
|
|
[0-0]
|
0
|
1,00
|
0,82
|
0,35
|
0,18
|
0,11
|
0,36
|
0,043
|
|
[0-34]
|
17
|
1,22
|
1,00
|
0,38
|
0,19
|
0,11
|
0,40
|
0,048
|
|
[34-253]
|
143,5
|
2,87
|
2,65
|
1,00
|
0,27
|
0,14
|
0,78
|
0,095
|
|
[253-440]
|
346,5
|
5,51
|
5,29
|
3,64
|
1,00
|
0,22
|
1,88
|
0,229
|
|
[440-789]
|
614,5
|
9,00
|
8,78
|
7,13
|
4,49
|
1,00
|
4,79
|
0,584
|
|
Total
|
|
|
|
|
|
|
8,21
|
1,000
|
X=5.195 ; IC=0.049 ; RC=0,044
Tableau 5.9: Calcul de matrice pour la population de
travailleur
|
Classe-
densité
|
Milieu-
classe
|
0
|
16,5
|
45,5
|
75,5
|
118
|
Wi
|
Ti
|
|
[0-0]
|
0
|
1,00
|
0,47
|
0,24
|
0,16
|
0,11
|
0,29
|
0,037
|
|
[0-33]
|
16,5
|
2,12
|
1,00
|
0,34
|
0,20
|
0,13
|
0,45
|
0,056
|
|
[33-58]
|
45,5
|
4,08
|
2,97
|
1,00
|
0,33
|
0,17
|
0,92
|
0,116
|
|
[58-93]
|
75,5
|
6,12
|
5,00
|
3,03
|
1,00
|
0,26
|
1,89
|
0,238
|
|
[93-143]
|
118
|
9,00
|
7,88
|
5,92
|
3,88
|
1,00
|
4,39
|
0,553
|
|
Total
|
|
|
|
|
|
|
7,94
|
1,000
|
X=5.226 ; IC=0.056 ; RC=0,050
47
Tableau 5.10: Calcul de matrice pour les
bâtiments en tuf
|
Classe-
densité
|
Milieu_ classe
|
0
|
2,9
|
8,15
|
14,3
|
24,15
|
Wi
|
Ti
|
|
[0-0]
|
0
|
1,00
|
0,51
|
0,27
|
0,17
|
0,11
|
0,31
|
0,038
|
|
[0-5,79]
|
2,9
|
1,96
|
1,00
|
0,37
|
0,21
|
0,12
|
0,45
|
0,056
|
|
[5,79-10,5]
|
8,15
|
3,70
|
2,74
|
1,00
|
0,33
|
0,16
|
0,88
|
0,110
|
|
[10,5-18,1]
|
14,3
|
5,74
|
4,78
|
3,04
|
1,00
|
0,23
|
1,81
|
0,227
|
|
[18,1-30,2]
|
24,15
|
9,00
|
8,04
|
6,30
|
4,26
|
1,00
|
4,55
|
0,569
|
|
Total
|
|
|
|
|
|
|
8,00
|
1,000
|
X=5.264 ; IC=0.066 ; RC=0,054
Tableau 5.11: Calcul de matrice pour les
bâtiments en bloc
|
Classe-
densité
|
Milieu- classe
|
0
|
3,17
|
9,17
|
14,85
|
21
|
Wi
|
Ti
|
|
[0-0]
|
0
|
1,00
|
0,45
|
0,22
|
0,15
|
0,11
|
0,28
|
0,035
|
|
[0-6,34]
|
3,17
|
2,21
|
1,00
|
0,30
|
0,18
|
0,13
|
0,44
|
0,055
|
|
[6,34-12]
|
9,17
|
4,49
|
3,29
|
1,00
|
0,32
|
0,18
|
0,97
|
0,122
|
|
[12-17,7]
|
14,85
|
6,66
|
5,45
|
3,16
|
1,00
|
0,30
|
2,03
|
0,257
|
|
[17,7-24,3]
|
21
|
9,00
|
7,79
|
5,51
|
3,34
|
1,00
|
4,19
|
0,530
|
|
Total
|
|
|
|
|
|
|
7,90
|
1,000
|
X=5.345 ; IC=0.086 ; RC=0,077
Tableau 5.12: Calcul de matrice pour les
bâtiments en bon état
|
Classe-
densité
|
Milieu-
classe
|
0
|
1,47
|
4,5
|
8,08
|
16,15
|
Wi
|
Ti
|
|
[0-0]
|
0,00
|
1,00
|
0,58
|
0,31
|
0,20
|
0,11
|
0,33
|
0,041
|
|
[0-2,94]
|
1,47
|
1,73
|
1,00
|
0,40
|
0,23
|
0,12
|
0,46
|
0,056
|
|
[2,94-6,06]
|
4,50
|
3,23
|
2,50
|
1,00
|
0,36
|
0,15
|
0,84
|
0,105
|
|
[6,06-10,1]
|
8,08
|
5,00
|
4,27
|
2,77
|
1,00
|
0,20
|
1,64
|
0,203
|
|
[10,1-22,2]
|
16,15
|
9,00
|
8,27
|
6,77
|
5,00
|
1,00
|
4,79
|
0,594
|
|
Total
|
|
|
|
|
|
|
8,06
|
1,000
|
X=5.194 ; IC=0.049 ; RC=0,043
Tableau 5.13: Calcul de matrice pour les
bâtiments en moyen état
|
Classe-
densité
|
Milieu_ Classe
|
0
|
1,82
|
5,66
|
10,8
|
18,95
|
Wi
|
Ti
|
|
[0-0]
|
0
|
1,00
|
0,57
|
0,30
|
0,18
|
0,11
|
0,32
|
0,040
|
|
[0-3,63]
|
1,82
|
1,77
|
1,00
|
0,38
|
0,21
|
0,12
|
0,44
|
0,055
|
|
[3,63-7,69]
|
5,66
|
3,39
|
2,62
|
1,00
|
0,32
|
0,15
|
0,84
|
0,105
|
|
[7,69-13,9]
|
10,8
|
5,56
|
4,79
|
3,17
|
1,00
|
0,23
|
1,80
|
0,224
|
|
[13,9-24]
|
18,95
|
9,00
|
8,23
|
6,61
|
4,44
|
1,00
|
4,65
|
0,577
|
|
Total
|
|
|
|
|
|
|
8,06
|
1,000
|
X=5.208 ; IC=0.052 ; RC=0,046
48
Tableau 5.14: Calcul de matrice pour les
bâtiments en mauvais état
|
Classe-
densité
|
Milieu_ classe
|
0
|
1,39
|
4,42
|
8,78
|
15,05
|
Wi
|
Ti
|
|
[0-0]
|
0
|
1,00
|
0,58
|
0,30
|
0,18
|
0,11
|
0,32
|
0,040
|
|
[0-2,77]
|
1,39
|
1,74
|
1,00
|
0,38
|
0,20
|
0,12
|
0,44
|
0,054
|
|
[2,77-6,06]
|
4,42
|
3,35
|
2,61
|
1,00
|
0,30
|
0,15
|
0,83
|
0,103
|
|
[6,06-11,5]
|
8,78
|
5,67
|
4,93
|
3,32
|
1,00
|
0,23
|
1,85
|
0,229
|
|
[11,5-18,6]
|
15,05
|
9,00
|
8,26
|
6,65
|
4,33
|
1,00
|
4,64
|
0,574
|
|
Total
|
|
|
|
|
|
|
8,07
|
1,000
|
X=5.242 ; IC=0.060 ; RC=0,054
|
|



