CHAPITRE 4
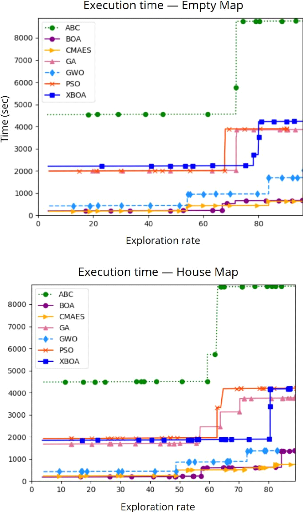
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.7 - Comparaison de la durée totale de la mission
d'exploration pour la stratégie à long terme
119
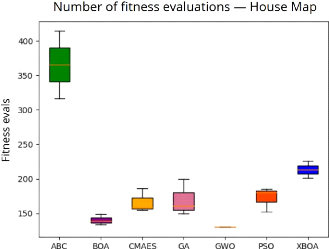
(a) Nombre d'évaluations de la fonction de fitness
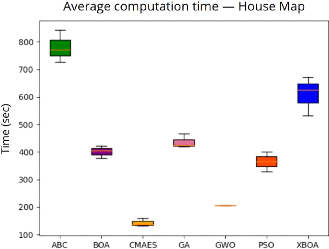
(b) Temps moyen de calcul pour chaque métaheuristique
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.8 - Nombre d'évaluations de la
fonction de fitness et temps moyen de calcul pour chaque
métaheuristique
120
CHAPITRE 4
4.7 Expérience 5 : Evaluation de la robustesse de
l'algo-rithme xBOA face à la réduction de taille de la
population
Afin d'étudier la possibilité
d'accélérer les algorithmes BOA et xBOA en réduisant la
taille de la population, nous avons effectué une série
d'expériences afin de mesurer l'in-fluence de la taille de la population
sur ces algorithmes et la robustesse de ces derniers.
Dans un premier temps, nous avons effectué une
expérience sur l'algorithme BOA original en variant la taille de la
population de 20 à 5 papillons tout en gardant les autres
paramètres fixes.
Les résultats présentés sur la figure 4.9
montrent que la réduction du nombre de solutions candidates (papillons)
réduit considérablement le temps d'exécution de la
métaheu-ristique. En effet, ce temps a diminué de 320 secondes
à 110 secondes en divisant la taille de la population en quatre.
Toutefois, ceci affecte aussi la qualité de l'exploration puisque
TABLE 4.3 - Evolution du taux d'exploration selon la taille de
la population en utilisant l'algorithme BOA
|
Short-term exploration - House map
|
|
Pop size
|
Average
|
Min
|
Max
|
|
05 butterflies
|
86.11
|
81.77
|
95.13
|
|
10 butterflies
|
88.66
|
79.68
|
95.13
|
|
20 butterflies
|
92.84
|
89.75
|
94.27
|
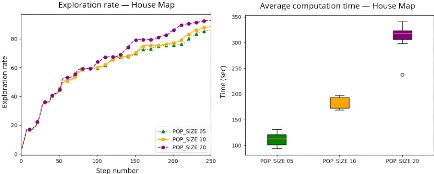
*Les résultats présentent les valeurs
moyennes de 3 exécutions
FIGURE 4.9 - Comparaison des résultats en utilisant
l'algorithme BOA avec différentes tailles de population sur
l'environnement House Map
121
le taux total de la surface explorée a baissé de
6.73%, tel que nous pouvons le voir sur le tableau 4.3.
Bien que cette baisse du taux d'exploration est importante, le
gain apporté de pouvoir calculer le prochain point de destination en
moins de 110 secondes apporte son lot d'avan-tages puisque ce temps d'attente
est acceptable pour beaucoup de scénarios de robotique dans le monde
réel par rapport au temps initial qui était trois fois plus
long.
En prenant ces résultats comme ligne de base, nous
avons effectué d'autres expériences pour mesurer les performances
de notre méthode ainsi que celles des autres métaheuris-tiques
lorsque la taille de la population est réduite à 5
solutions. Les résultats sont présentés sur le
tableau 4.3 et les figures 4.10 et 4.11.
La première remarque notable que nous pouvons constater
en observant les graphes se trouve au niveau du taux d'exploration des
méthodes PSO et GWO dont l'amélioration s'est
arrêtée après avoir atteint les valeurs de 75% et
62% respectivement, malgré qu'elles démontraient des
résultats proches de ceux des autres méthodes lorsque la taille
de la population était plus grande.
La deuxième observation notable c'est que la surface de
la zone visitée à la fin de la mission n'a pas pu dépasser
le taux de 97% pour l'environnement Empty Map et 93.35%
pour l'environnement House Map, et ceci, même si le niveau
d'énergie du robot n'a pas encore atteint 0. Après la
visualisation des trajectoires des robots dans le simulateur, nous avons
remarqué que ceci est dû au blocage des robots dans un minima
local où ils revisitent des régions déjà
explorées. Ceci s'explique par le manque de diversification dans les
solutions puisque le nombre très réduit de la population a
engendré une convergence prématurée vers une solution
unique. C'est-à-dire que tous les cinq individus de la population
avaient (presque) la même valeur.
Une potentielle solution pour éviter ce problème
serait d'augmenter l'espace de recherche graduellement en augmentant la taille
de la population lorsque le taux de la surface explorée dépasse
un certain seuil (par exemple 80%). En d'autres termes : commencer la recherche
en utilisant une taille de population réduite afin
d'accélérer le temps de calcul, puis augmenter le nombre
d'individus à la fin de la mission pour diversifier la population et
échapper aux minimas locaux. Ceci devrait être une meilleure
stratégie pour profiter des avantages des deux paramétrages, sans
sacrifier la qualité du résultat obtenu à la fin de la
mission.
Nous observons également que la méthode xBOA
domine toutes les autres méthodes sur les critères du taux
d'exploration et de la convergence de la valeur de fitness, mais elle souffre
d'un temps d'exécution élevé. De l'autre
côté, la méthode CMAES est dominante sur le critère
du temps moyen de calcul qui avoisine les 25 secondes, mais elle
souffre d'un taux d'exploration inférieur à xBOA de 10%. La
méthode ABC est la plus lente de toutes les méthodes, elle
nécessite 175 secondes de temps de calcul pour arriver à
un résultat presque similaire à celui de xBOA. Tandis que GA
offre un bon compromis entre qualité et vitesse d'exécution. La
figure 4.12 montre la différence de ces résultats avec
ceux obtenus lors de la série d'expériences
précédente qui utilisait une taille de population de 20
individus.
Étant donné que la méthode xBOA a pu
garder un taux d'exploration supérieur aux
122
| 


