CHAPITRE 2
autoadaptative qui ne nécessite plus l'utilisation des
deux paramètres c (sensory modality) et a (power exponent).
Cette nouvelle variante est appelée SABOA (Self-Adaptative
BOA). D'un autre côté, les auteurs de [44] ont modifié
l'équation de la recherche globale dans le but d'améliorer la
convergence de l'algorithme, couplé avec une stratégie de
réinitialisation périodique de la population afin d'éviter
le blocage dans un minima local.
Les variantes citées ci-haut ont montré des
résultats prometteurs pour la résolution des problèmes
d'optimisation globaux à grandes dimensions, ce qui constituait une des
faiblesses de l'approche BOA classique. Une autre faiblesse consiste en la
lenteur de la convergence de l'algorithme causée par le faible taux de
diversité des solutions dans la population.
Pour résoudre ces deux problèmes, nous proposons
de modifier la méthode en introduisant l'opérateur de croisement
et modifiant la stratégie de mouvement des papillons dans les phases de
recherches globale et locale. Ces changements ont permis l'introduction d'une
nouvelle variante de l'algorithme appelée xBOA (crossover BOA)
[16].
La figure 2.15 résume l'état de l'art des variantes
de BOA citées ci-haut.
FIGURE 2.15 - Résumé de l'état de l'art de
l'algorithme BOA et ses différentes variantes
75
2.9 Amélioration de l'Algorithme d'Optimisation des
Papillons en utilisation l'opérateur de croisement (xBOA)
L'équation 2.7 déplace tous les papillons vers
la meilleure solution de la population, ce qui ignore les autres solutions qui
ont la même valeur de fitness ou qui ont le potentiel de devenir de
meilleures solutions après quelques itérations. Afin de
dépasser cette limitation, nous proposons de modifier l'algorithme BOA
en remplaçant cette équation avec l'opérateur de
croisement durant la phase de recherche globale.
L'opérateur de croisement a été introduit
dans l'Algorithme Génétique [41]. Il consiste à combiner
deux individus parents pour créer de nouveaux individus appelés
enfants (ou offsprings en anglais). L'idée de base
inspirée de la nature simule la manière dont les enfants
héritent une partie des caractéristiques de chaque parent.
Plusieurs stratégies de combinaisons ont
été proposées dans la littérature [69]. Pour des
raisons de simplicité, nous allons utiliser la stratégie de
croisement à un point (Single-point Crossover). Elle consiste
à diviser le vecteur de données du premier parent en deux
sous-vecteurs, puis les permuter avec les sous-vecteurs du deuxième
parent afin de produire deux nouveaux individus.
L'exemple présenté dans la figure 2.16 montre le
résultat de cette opération pour deux individus de taille 5 ainsi
que le pseudo-code de cette opération.
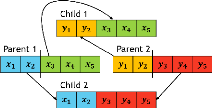

FIGURE 2.16 - Exemple et pseudo-code de l'opérateur de
croisement
76
| 


