CHAPITRE 2
Vu que l'insertion de nouveaux individus dans la population
peut rapidement faire croître sa taille, nous avons choisi de remplacer
un individu parent par un de ses enfants; le meilleur enfant est choisi dans ce
cas. Ceci nous permet de garder une taille de population fixe pendant toute la
durée du processus d'optimisation.

FIGURE 2.17 - Pseudo-code de l'algorithme xBOA
En utilisant l'opérateur de croisement, nous
encourageons les papillons à se déplacer vers plusieurs
potentielles solutions au lieu de converger tous vers la meilleure solution
connue. Ceci crée une diversité dans la population et permet
à l'algorithme d'échapper au piège de converger
prématurément vers un minima local. En d'autres termes, la
population de papillons va inspecter plusieurs régions de l'espace de
recherche simultanément afin de
77
trouver la solution globale plus rapidement.
L'utilisation de l'opérateur de croisement à
chaque itération pourrait toutefois déséquilibrer la
balance entre les propriétés d'exploration et d'exploitation de
l'algorithme xBOA, nous utilisons donc un paramètre qui
déterminera à quelle fréquence cet opérateur est
utilisé. Ce paramètre est appelé probabilité de
croisement (crossover probability). Il remplacera le paramètre
Switch Probability utilisé dans l'algorithme BOA original.
Une autre différence entre les deux algorithmes se
situe au niveau de la recherche locale. En effet, dans xBOA l'équation
2.8 est utilisée même si elle engendre une dégradation de
la qualité des solutions, contrairement à l'algorithme original.
Ceci semble contre-productif, néanmoins cela permet à
l'algorithme d'augmenter la diversité des solutions en leur permettant
de se déplacer aléatoirement dans l'espace de recherche et
d'explorer de nouvelles régions qui pourraient cacher la solution
globale. La stratégie est d'accepter une perte en qualité
à court terme pour pouvoir découvrir des solutions encore
meilleures que celles trouvées jusqu'ici.
Les résultats des expériences effectuées
durant notre thèse ont montré que les modifications
proposées ont permis à xBOA de trouver la solution globale plus
rapidement que l'algorithme BOA original, et d'être plus robuste aux
minima locaux.
Le diagramme de la figure 2.18 décrit toutes les
opérations de l'algorithme xBOA, son pseudo-code est
présenté dans la figure 2.17.
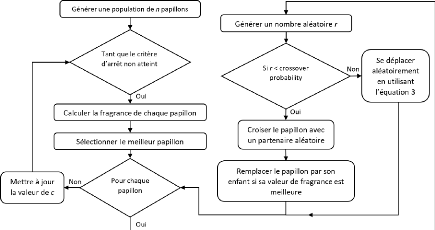
FIGURE 2.18 - Diagramme de l'algorithme xBOA
78
CHAPITRE 2
2.10 Conclusion
Nous avons présenté dans ce chapitre le principe
de fonctionnement des métaheuris-tiques et leurs mécanismes
internes. Nous avons également présenté les fondements
théoriques de plusieurs métaheuristiques populaires
utilisées dans la littérature pour résoudre divers
problèmes d'optimisation globale, dont les problèmes de
robotique.
Ce chapitre a aussi présenté les fondements
mathématiques de la méthode BOA (Butterfly Optimization
Algorithm) ainsi que ses avantages et limitations. Nous avons
proposé des modifications visant à l'améliorer ce qui a
donné lieu à une nouvelle variante de l'algo-rithme que nous
avons appelé xBOA (crossover Butterfly Optimization
Algorithm).
Cette variante se base sur l'intégration de
l'opérateur de croisement durant la recherche globale afin de lui
permettre de diversifier les solutions et échapper aux optimums locaux.
Elle intègre aussi une modification dans la stratégie de la
recherche locale pour éviter de converger trop rapidement vers un
optimum local.
Ce chapitre conclut la partie théorique de notre
thèse. Les deux autres chapitres restants seront consacrés
à l'étude expérimentale.
79
Deuxième partie
Etude expérimentale

80
| 


