CHAPITRE 2
68
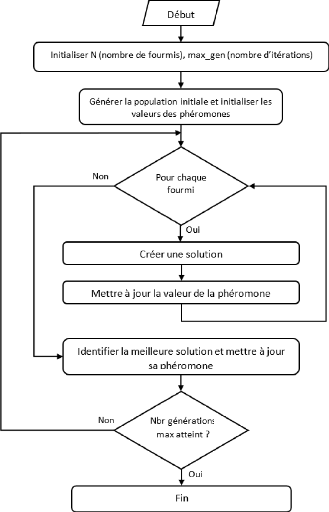
FIGURE 2.12 - Pseudo-code de l'algorithme ACO
69
Après un certain nombre d'itérations, les
solutions les plus visitées auront une quantité de
phéromones plus grande, ce qui augmente la probabilité que les
fourmis les choisissent. La baisse régulière de la
quantité de phéromones permet aux fourmis d'explorer des
solutions différentes pendant le processus de recherche. C'est un
mécanisme de diversification sans lequel l'algorithme risque de
converger rapidement vers un optimum local. Un autre mécanisme est de
garder en mémoire la liste des solutions que la fourmi a
déjà visitées, de sorte à les éliminer dans
ses futurs mouvements.
2.7 Les Fondements théoriques de l'Algorithme
d'Opti-misation des Papillons (BOA)
Butterfly Optimization Algorithm (BOA) est une
métaheuristique à base de populations s'inspirant du comportement
des papillons, elle a été proposée par S. Arora
et S. Singh [11] en tant qu'algorithme d'optimisation globale.
Au départ, l'algorithme génère une
population de solutions aléatoires (les papillons), puis les modifie
à travers plusieurs itérations jusqu'à ce qu'un
critère d'arrêt soit atteint.
Dans la nature, les papillons utilisent l'odorat pour trouver
des sources de nourriture et des partenaires de reproduction, pour y arriver,
ils utilisent des cellules dans leurs corps pour percevoir les odeurs
(fragrance) et mesurer leurs intensités [11]. Plus la fragrance
est intense, plus le papillon est attiré vers la source de cette
odeur.
L'algorithme BOA modélise ce comportement en calculant
une valeur de fragrance proportionnelle à la valeur de fitness de
l'individu. Plus la valeur de fitness d'un papillon est de meilleure
qualité, plus sa fragrance est grande, et plus les autres papillons y
sont attirés. Toutefois, la fragrance émise par un papillon dans
la nature est souvent altérée par les conditions
météorologiques. Deux paramètres sont donc introduits dans
l'algorithme pour simuler ce phénomène et modifier
l'intensité de la fragrance qui sera captée par les autres
papillons.
Ces paramètres sont les suivants:
-- Sensor modality (c) : Un facteur de multiplication
contrôlant la proportion de la fragrance qui sera perçue.
-- Power exponent (a) : Un exposant qui
contrôle la puissance à laquelle l'intensité originale de
la fragrance est amplifiée.
L'équation 2.6 décrit la règle de calcul de
la fragrance:
F = c * Ia (2.6)
Où :
-- c = sensor modality;
-- a = power exponent; et
-- I = intensité originale de la fragrance, qui est
égale à la valeur de fitness du papillon.
CHAPITRE 2
Générer une population de n papillons
Calculer la fragrance de chaque papillon
Sélectionner le meilleur papillon
r N
Mettre à jour
la valeur de c
ti
Générer un nombre aléatoire r
Non
Se déplacervers le meilleur papillon en utilisant
l'équation 2
i
Remplacer l'ancienne solution par la
nouvelle si
meilleure
N
Se déplacer aléatoirement en
utilisant
l'équation 3
70
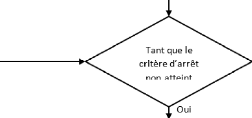
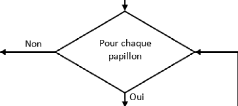
FIGURE 2.13 -- Diagramme de l'algorithme
BOA
71
Une fois les fragrances calculées, les papillons vont
se déplacer graduellement vers le meilleur papillon qui
représente la meilleure solution trouvée jusqu'à
présent dans l'espace de recherche. Cette étape est
appelée « recherche globale » [11]
Afin d'éviter une convergence prématurée,
une phase de recherche locale a été introduite par les auteurs de
l'algorithme pendant laquelle les papillons se déplacent
aléatoirement dans la région où ils se trouvent.
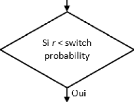
À chaque itération, l'algorithme
exécutera soit la phase de recherche globale, soit celle de la recherche
locale, selon la valeur d'une probabilité d'alternance (switching
probability).
Les équations suivantes décrivent respectivement
comment les individus sont mis à jour pendant les phases de recherche
globale et locale:
xt+1
i = xt i + (r2 * g* - xt
) * fi (2.7)
i
xt+1
i = xt i + (r2 * xt j - xt )
* fi (2.8)
k
Où :
-- xi est le papillon n° i;
-- r est un nombre aléatoire appartenant à
l'interval [0, 1];
-- g* est le meilleure papillon dans la population;
-- fi est la fragrance du papillon n° i;
-- xj et xk sont deux papillons sélectionnés
aléatoirement parmi la population.
En exécutant l'équation 2.7 plusieurs fois
à travers les itérations, les papillons convergeront vers
l'individu ayant la meilleure valeur de fitness qui représente la
meilleure solution connue. Toutefois, une convergence trop rapide pourrait
piéger les individus dans le voisinage d'un optimum local alors qu'une
meilleure solution se trouve ailleurs dans l'espace de recherche.
L'équation 2.8 évite à ce problème en poussant les
papillons à se déplacer aléatoirement pour explorer de
nouvelles solutions.
À chaque itération, les valeurs de fitness des
papillons augmenteront en qualité, et leurs fragrances seront de plus en
plus grandes. Afin d'éviter une convergence trop rapide engendrée
par une trop grande augmentation de la fragrance, les auteurs de l'algorithme
ont introduit une règle pour diminuer le facteur de multiplication c
(sensor modality) à la fin de chaque itération [9].
L'ajout de cette règle - décrite par l'équation 2.9 - leur
a permis d'améliorer les résultats de l'algorithme.
f 0.025 )
ct+1 = ct + (2.9)
ct * nbr_iterations
72
| 


