CHAPITRE 2
2.5 Structure de base d'une métaheuristique
Malgré la diversité des métaheuristiques et
leurs types, elles partagent toutes la même structure de base.
L'algorithme de base d'une métaheuristique se découpe en 3
parties:
2.5.1 La phase d'initialisation
Cette phase est exécutée une seule fois au
début de l'algorithme, son but est de définir toutes les
variables et les paramètres nécessaires pour son bon
fonctionnement. Ceci implique généralement d'effectuer les
actions suivantes:
-- Définir le problème : taille de la population,
dimensions des individus, contraintes.
-- Définir la fonction objectif et ses
paramètres.
-- Définir les autres hyperparamètres : nombre
d'itérations, critère d'arrêt...etc.
-- Générer la solution - ou la population de
solutions - initiale.
-- Evaluer les solutions initiales en utilisant la fonction
objectif.
2.5.2 Le corps de l'algorithme
Il s'agit d'exécuter les opérations constituant le
coeur du processus d'optimisation. Cette phase est répétée
jusqu'à ce que le critère d'arrêt soit atteint:
-- Exécuter l'ensemble des opérations constituant
la logique de l'algorithme. -- Evaluer la qualité des solutions.
-- Mémoriser la meilleure solution trouvée
jusqu'ici.
-- Répéter les opérations jusqu'à ce
que le critère d'arrêt soit atteint.
2.5.3 La phase finale
C'est la dernière phase qui sera exécutée
lorsque le processus d'optimisation est terminé. Elle comprend
généralement des actions d'aide à l'analyse des
résultats:
-- Sauvegarder les résultats : meilleure solution,
qualité de la solution finale, temps d'exécution...etc.
-- Tracer les graphes de performances, historique
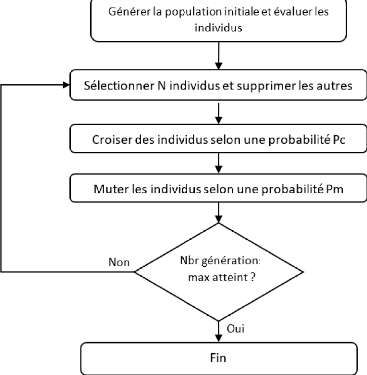
d'évolution de la fonction objectif...etc. La figure 2.10
schématise la structure de base d'une métaheuristique.
63
Début
Initialiser N (nombre d'individus), max gen (nombre
d'itérations), Pc (probabilité de croisement), et Pm
(probabilité de mutation)
t
Sélectionner N individus et supprimer les
autres
Nbr génération: max atteint ?
Générer la population initiale et évaluer
les individus
Croiser des individus selon une probabilité
Pc
Muter les individus selon une probabilité Pm
Fin
FIGURE 2.10 -- Structure de base d'une
métaheuristique
64
CHAPITRE 2
2.6 Fondements théoriques de métaheuristiques
populaires
Dans cette section, nous allons présenter les
fondements théoriques et le principe de fonctionnement de quelques
métaheuristiques populaires. Ces métaheuristiques seront
utilisées dans les chapitres suivants lors des expériences de
benchmarking et de résolution du problème d'exploration
multirobots.
Les algorithmes seront présentés en suivant l'ordre
chronologique de leur apparition.
2.6.1 Les algorithmes génétiques (GA)
Les Algorithmes Génétiques utilisent des
concepts issus de la génétique et de la sélection
naturelle. Ils ont été introduits par les travaux de John Holland
[75] et D. Goldberg [41].
La population dans un algorithme génétique est
constituée d'un certain nombre d'indi-vidus, eux-mêmes
constitués d'un ensemble de gènes (regroupés en
chromosomes). Un gène représente une variable spécifique
au problème qu'on veut optimiser et est généralement
codé par un nombre binaire ou réel.
Les individus dans cet algorithme sont soumis aux 3
opérations suivantes: Sélection
Durant cette opération, les meilleurs candidats sont
choisis pour servir de parents à la génération
suivante. Ce processus est similaire au processus de sélection naturelle
: les individus les plus adaptés à leur environnement
sont conservés tandis que les moins adaptés meurent avant la
reproduction.
Toutefois, des stratégies sont parfois mises en place
pour conserver certains individus de mauvaise qualité afin de
diversifier la population et éviter une convergence trop rapide vers
l'optimum local.
L'adaptation d'un individu est calculée en fonction de
sa valeur de fitness. L'opération de sélection nécessite
donc d'évaluer l'ensemble des individus de la population à
chaque itération afin de pouvoir les comparer, ce qui a un impact
sur la complexité globale de l'algorithme. Pour une population de N
individus et M itérations, la complexité sera
égale à N x M.
Croisement (crossover)
Cette opération est parfois appelée
reproduction, elle vise à combiner deux individus au
hasard afin d'en produire d'autres. Pour ce faire, l'algorithme
sélectionne quelques gènes
65
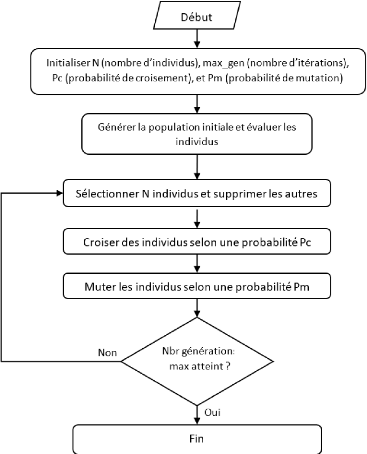
FIGURE 2.11 - Diagramme de l'algorithme
génétique
66
| 


