CHAPITRE 2
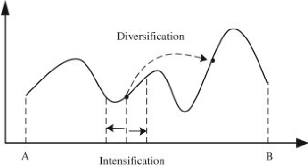
FIGURE 2.7 - Difference entre les
stratégies d'exploration et d'exploitation d'une métaheu-ristique
[70]
2.4.3 La convergence
On dit qu'une métaheuristique converge, lorsque la
majorité des individus constituant sa population aboutissent à la
même solution (voir figure 2.8).
Cette convergence est le résultat d'une comparaison
avec différentes solutions trouvées de l'espace de recherche,
puis l'élimination des solutions de mauvaise qualité, de sorte
à ne garder à la fin que la solution optimale.
Dans le cas idéal, la convergence vers la meilleure
solution se fait après que l'algorithme ait exploré toutes les
régions de l'espace de recherche afin de garantir de tomber sur la
solution optimale. On appelle cette solution Optimum Global ou
Minima Global. Toutefois, il se pourrait dans certains cas que
l'algorithme converge vers une certaine région sans avoir exploré
d'autres, et pourra donc rater la solution optimale en convergeant vers une
solution de moindre qualité. On appelle cette solution Optimum Local
ou Minima Local.
L'objectif d'une métaheuristique est donc de trouver un
compromis entre les phases d'exploration et d'exploitation afin d'éviter
de converger trop rapidement vers un optimum local, mais sans pour autant
perdre trop de temps à explorer chaque région en détail.
L'idée est d'éliminer les mauvaises régions rapidement
afin de pouvoir se concentrer sur les régions les plus prometteuses.
D'un point de vue mathématique, une solution
s* est appelée optimum global si et seulement si
elle respecte l'équation 2.2.
f(s*) f(s)Vs E S. (2.2)
Sachant que S est l'espace de recherche et f : S ?- R+ 0 est la
fonction objectif à minimiser.
59
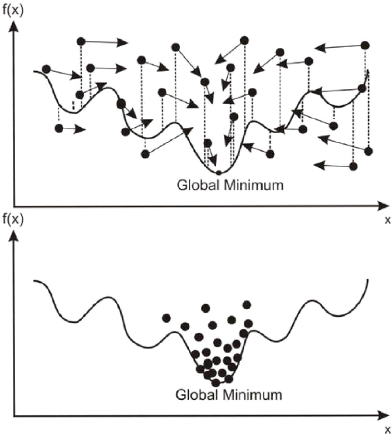
FIGURE 2.8 - Exemple de convergence d'une
population de solutions [21]
2.4.4 Les hyperparamètres
Ce sont les paramètres spéciaux que l'utilisateur
doit définir manuellement pour réguler le comportement de
l'algorithme. Ces hyperparamètres sont définis avant le
début de l'exécution, souvent de manière
expérimentale en essayant plusieurs combinaisons.
Parmi les hyperparamètres les plus utilisés dans
les métaheuristiques, nous retrouvons:
-- La taille de la population : qui représente le nombre
d'individus (ou nombre de solutions candidates).
-- La taille de l'individu : nombre de variables constituant une
solution.
60
CHAPITRE 2
-- Nombre d'itérations : nombre maximal
d'itérations avant l'arrêt de l'algorithme. -- Le taux de mutation
: probabilité à laquelle une solution est modifiée.
-- ...etc.
2.4.5 Les contraintes
Des contraintes peuvent être ajoutées à la
modélisation d'un problème d'optimisation. Ces contraintes
divisent l'espace de recherche en deux catégories : d'une part
l'ensemble des solutions valides satisfaisant toutes les contraintes du
problème, d'autre part l'ensemble des solutions non valides où au
moins une contrainte est violée.
Le moyen le plus simple pour intégrer une contrainte
à la fonction objectif d'un problème est d'ajouter un facteur qui
pénalise les solutions non conformes. Ceci prend
généralement la forme d'une multiplication entre le nombre de
contraintes violées et un paramètre de pénalité
fixé manuellement par l'utilisateur.
2.4.6 Les générations
Les métaheuristiques se basent sur un principe de
répétition d'un ensemble d'opéra-tions. Suivant l'analogie
des algorithmes évolutionnaires, une itération dans le
contexte des métaheuristiques à base de population est souvent
appelée génération ou
évolution.
Le principe est qu'à chaque génération,
la population subit plusieurs transformations de sorte qu'elle devienne
meilleure que ce qu'elle n'était durant la génération
précédente.
Le meilleur individu de la dernière
génération constitue donc la meilleure solution trouvée au
cours du processus d'optimisation. Il est parfois appelé le
champion.
2.4.7 Les critères d'arrêt
Les métaheuristiques étant un processus
itératif, des critères d'arrêts doivent être mis en
place afin d'éviter le prolongement de l'exécution de
l'algorithme indéfiniment.
Les critères d'arrêts les plus populaires
utilisés dans le domaine de l'optimisation combinatoire sont les
suivants:
-- Atteindre un nombre maximal d'itérations.
-- Atteindre un nombre maximal de solutions
évaluées en utilisant la fonction objectif.
-- Atteindre un nombre maximal d'itérations où
aucun changement n'a été mesuré sur les valeurs de la
fonction objectif (early stopping).
-- Atteindre une certaine valeur de la fonction fitness.
61
2.4.8 L'optimalité et la dominance
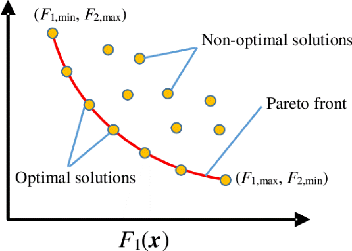
FIGURE 2.9 - Visualisation d'un front optimal
(Pareto Front) séparant les solutions dominées des solutions non
dominées [65]
Les métaheuristiques peuvent résoudre des
problèmes d'optimisation ayant plusieurs objectifs contradictoires.
Une stratégie est de réduire ces objectifs
à un seul facteur d'optimisation en utilisant une somme
pondérée. Une autre stratégie consiste à garder ces
objectifs contradictoires et explorer plusieurs espaces de recherches en
parallèle, selon le nombre d'objectifs à optimiser.
Lorsque l'algorithme optimise un problème
mono-objectif, la meilleure solution est celle qui obtient la meilleure valeur
de fitness.
Dans le cas d'une optimisation multi-objectifs nous pouvons
avoir deux cas de figure: soit une solution obtient la valeur optimale dans
tous les espaces de recherches, nous disons donc que cette solution domine les
autres solutions. Soit, nous nous retrouvons avec plusieurs solutions, chacun
domine l'autre dans un objectif en particulier, mais pas dans l'autre. Ces
solutions sont donc toutes les deux optimales et on les appelle solutions non
dominées. L'ensemble des solutions non dominées est appelé
Pareto-front. La figure 2.9 illustre ceci d'une manière graphique.
62
| 


