CHAPITRE 2
Une autre méthode populaire dans cette catégorie
est appelée Optimisation par Essaim de Particules (PSO : Particle
Swarm Optimization) [58]. Elle imite le comportement social de groupe de
poissons et d'oiseaux en vol où chaque individu modifie sa direction de
mouvement en réponse à ses propres expériences et à
celles de ses voisins. Elle a été appliquée avec
succès dans de nombreux domaines et a donné des résultats
satisfaisants, en particulier pour les problèmes non
linéaires.
Le nombre de métaheuristiques qui rentre dans la
catégorie de l'intelligence en essaim ne cesse de croître, et il
est difficile de toutes les citer. Il s'agit d'un axe de recherche très
actif puisant sa source d'inspiration de la nature. Citons par exemple les
algorithmes d'op-timisation inspirés du comportement des abeilles par
exemple (ABC : Artificial Bee Colony) [55], les loups (GWO : Grey
Wolf Optimizer) [66], les chauves-souris (Bat Algorithm) [91],
les lucioles (Firefly Algorithm)[93]...etc.
Algorithmes inspirés de la physique
Il s'agit d'un type d'algorithmes à base de populations
-toujours inspiré de la nature-mais cette fois des
phénomènes physiques. Ces techniques suivent les mêmes
principes que les algorithmes d'intelligence en essaim et sont parfois
considérées comme une sous-catégorie de ceux-ci.
Parmi ces algorithmes nous retrouvons ceux basés sur
les principes d'interaction entre les masses telles que l'algorithme de
recherche à gravitation (GSA : Gravitational Search Algorithm)
[71] dont les équations sont inspirées de la loi de la
gravité de Newton.
La population de solution dans cet algorithme est
représentée par un ensemble d'atomes qui interagissent entre eux
proportionnellement à leurs masses. Plus une solution sera de meilleure
qualité, plus sa masse augmentera et attirera donc les autres atomes
vers elle.
Nous retrouvons aussi des méthodes basées sur
les principes de la mécanique des fluides, telles que le Vortex
Search Algorithm [30]. Ainsi que d'autres inspirées des principes
d'élec-tromagnétisme tel que l'algorithme des champs
électriques artificiels (Artificial Electric Field Algorithm)
[88].
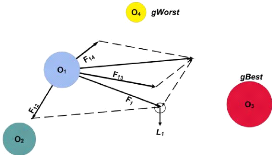
56
FIGURE 2.6 - Optimisation à base d'interactions
physiques entre les atomes [67]
57
2.4 Les mécanisme des métaheuristiques
2.4.1 La fonction objectif
Une fonction d'évaluation - communément
appelée fonction objectif ou fonction fitness - est
une fonction mathématique qui évalue la qualité d'une
solution dans un problème d'optimisation spécifique.
Elle prend une solution candidate en entrée et retourne un
nombre scalaire (voir équation 2.1). Ce scalaire sera utilisé par
l'algorithme pour comparer les solutions trouvées et sélectionner
la meilleure. De ce fait, elle dirige le processus de recherche de
l'algorithme.
En d'autres termes, pour chaque solution s E S(I), une
valeur de fitness f(s) existe définie par la
formulation suivante:
f : S -? R (2.1)
0
s = {Xi/i = 1..n}
Sachant que S est l'espace de recherche à n
dimensions lié à notre problème, et I est l'ensemble
des contraintes du problème.
2.4.2 L 'exploration et l'exploitation
L'exploration et l'exploitation sont deux concepts clés
des métaheuristiques qui doivent constamment être balancées
afin de garantir une bonne convergence vers la solution optimale.
L'exploration, aussi appelée diversification,
est l'habilité de l'algorithme à diversifier les solutions en
couvrant plusieurs régions de l'espace de recherche. Tandis que
l'exploitation, aussi appelée intensification, est l'aptitude
à se concentre sur une seule région de l'espace de recherche dans
le but d'améliorer une solution en cherchant une meilleure solution dans
son voisinage.
La figure 2.7 schématise cette différence. La
phase d'intensification revient donc à faire une recherche locale. Alors
que la phase de diversification à pour but d'explorer l'espace de
manière générale.
58
| 


