CHAPITRE 2
Elle pourra être acceptée avec une certaine
probabilité afin de permettre à l'algorithme d'éviter un
blocage dans une région non optimale, tel que l'on peut voir dans
l'exemple présenté dans la figure 2.2.
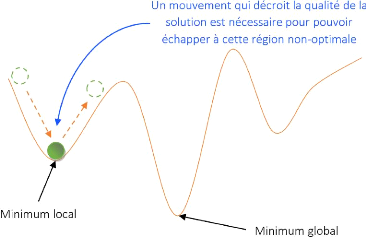
FIGURE 2.2 - Exemple d'une recherche à solution
unique
Ces méthodes se basent généralement sur
des stratégies de recherche locale et recherche de voisinage
couplée avec des mécanismes de mémorisation ou de sauts
[64]
Parmi les méthodes les plus connues de cette
catégorie, nous pouvons citer les suivantes:
-- La méthode du recuit simulé
(Simulated Annealing) [59]
Inspirée de la technique de traitement des
métaux, cet algorithme choisit à chaque étape s'il faut
accepter de déplacer la solution vers un état voisin qui risque
de décroître sa qualité ou s'il faut maintenir le
même état.
Ce choix se fait sur la base d'un calcul de probabilité
dont la valeur décroît régulièrement après
chaque itération jusqu'à atteindre zéro. En d'autres
termes, l'algorithme aura de moins en moins de chances d'accepter les mauvaises
solutions au fur et à mesure que le nombre d'itérations augmente.
Il finira par converger vers une solution de meilleure qualité.
-- La recherche tabou (Tabu Search)
[40]
Cet algorithme se base sur une recherche locale, tout en
évitant activement les points de l'espace de recherche
déjà visités. Ceci se fait en gardant en mémoire
ces points visités dans le but d'éviter les boucles dans les
trajectoires de recherche qui conduiront vers le blocage dans un minimum
local.
53
-- La recherche guidée (Guided Local Search)
[27]
Cet algorithme se base sur une recherche locale classique,
à la différence que lors-qu'un minimum local est
détecté (aucune amélioration de la qualité de la
solution n'est possible), une pénalité est rajoutée
à la fonction objective de sorte à encourager la solution
à sortir du voisinage courant et passer vers un nouveau voisinage.
2.3.2 Les méthodes à base de population
Ce type de méthodes démarre avec une population
de solutions et les améliore toutes en même temps afin d'explorer
plusieurs régions de l'espace de recherche en parallèle. Ceci
permet une plus grande flexibilité et une robustesse plus
élevée par rapport aux minimas locaux (voir figure
2.3).
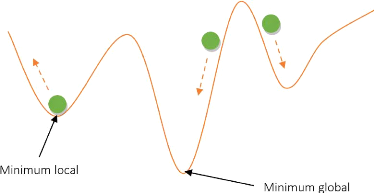
FIGURE 2.3 - Exemple d'une recherche à
base de population de solutions
Le choix de la population initiale est crucial pour la
réussite du processus d'optimisation. En effet, si toutes les solutions
de la population initiale sont presque identiques, il n'y aura pas suffisamment
de diversité et elles convergeront prématurément vers la
même solution.
Généralement les solutions sont
initialisées aléatoirement, cependant, des heuristiques peuvent
être utilisées pour influencer cette initialisation de
façon à avoir une population suffisamment diversifiée pour
pouvoir explorer la plus grande partie de l'espace de recherche.
Les méthodes à base de population peuvent
être classées en plusieurs catégories selon le type
d'inspiration:
| 


