CHAPITRE 2
LES MÉTAHEURISTIQUES
2.1 Introduction 50
2.2 Les métaheuristiques 50
2.3 Les types de métaheuristiques 51
2.3.1 Les méthodes à base de trajectoires
51
2.3.2 Les méthodes à base de population 53
2.4 Les mécanisme des métaheuristiques 57
2.4.1 La fonction objectif 57
2.4.2 L'exploration et l'exploitation 57
2.4.3 La convergence 58
2.4.4 Les hyperparamètres 59
2.4.5 Les contraintes 60
2.4.6 Les générations 60
2.4.7 Les critères d'arrêt 60
2.4.8 L'optimalité et la dominance 61
2.5 Structure de base d'une métaheuristique 62
2.5.1 La phase d'initialisation 62
2.5.2 Le corps de l'algorithme 62
2.5.3 La phase finale 62
2.6 Fondements théoriques de métaheuristiques
populaires 64
2.6.1 Les algorithmes génétiques (GA) 64
2.6.2 L'optimisation par Essaim de Particules (PSO) 66
2.6.3 L'otimisation par Colonie de Fourmies (ACO) 67
2.7 Les Fondements théoriques de l'Algorithme
d'Optimisation des
Papillons (BOA) 69
2.8 Les variantes de l'algorithme BOA 73
2.9 Amélioration de l'Algorithme d'Optimisation des
Papillons en uti-
lisation l'opérateur de croisement (xBOA) 75
2.10 Conclusion 78
50
CHAPITRE 2
2.1 Introduction
L'optimisation dans le domaine mathématique est un
terme utilisé pour désigner la recherche de la meilleure solution
à un problème donné. L'optimisation peut être
considérée comme un processus essayant de répondre
à la question suivante: « existe-t-il ou non une meilleure solution
au problème? ».
Nous allons présenter dans ce chapitre une famille de
méthodes utilisées dans le domaine de l'optimisation
numérique qui ont connu un grand succès durant le
demi-siècle dernier en raison de leur capacité à s'adapter
à différents types de problèmes et fournir des
résultats satisfaisants.
Nous introduisons aussi dans ce chapitre les fondements
théoriques d'une nouvelle technique appelée xBOA [16] et qui
constitue l'une des contributions principales de cette thèse.
2.2 Les métaheuristiques
Avec l'augmentation rapide des ressources de calcul
introduites par les ordinateurs, le besoin de résoudre des
problèmes plus complexes est devenu de plus en plus important. Des
techniques d'optimisation stochastique ont été
développées pour fournir des solutions efficaces à ce type
de problèmes.
Les heuristiques sont une classe d'algorithmes visant à
trouver des solutions approximatives à des problèmes
d'optimisation dont la complexité est combinatoire. L'optimisation
stochastique est un type de techniques d'optimisation se basant sur une
recherche aléatoire afin d'explorer plus efficacement l'espace de
solutions possibles.
Les métaheuristiques combinent le concept d'heuristique
avec l'optimisation stochastique dans le but de trouver des solutions
acceptables à des problèmes non linéaires dans un
intervalle de temps raisonnable comparé aux techniques de programmation
mathématique traditionnelles qui garantissent l'optimalité, mais
peuvent entraîner une explosion du temps d'exécution [57].
Le succès des métaheuristiques est causé
par leur capacité à résoudre des problèmes à
très haute complexité ainsi que des problèmes
d'optimisation ayant des objectifs contradictoires. Elles peuvent
également gérer des contraintes non linéaires et
être appliquées à une variété de
problèmes du monde réel sans nécessiter de gros changement
du point de vue de la programmation. Un autre avantage important des
métaheuristiques est leur capacité à résoudre des
problèmes dont le formalisme mathématique n'est pas connu avec
précision.
Toutefois, elles peuvent être coûteuses en temps
de calcul dans certains cas et ne garantissent pas toujours de trouver la
solution optimale. De plus, elles sont difficiles à paramé-trer
à cause de leur sensibilité aux valeurs initiales, ce qui peut
amener à une convergence prématurée.
Elles fournissent un moyen efficace pour trouver des solutions
optimales lorsque l'es-
51
pace de recherche est trop grand ou lorsque les données
sont incomplètes. Elles sont facilement adaptables et peuvent être
utilisées dans une variété de domaines, tels que
l'ingénierie, l'informatique, l'économie ou les finances.
2.3 Les types de métaheuristiques
Les métaheuristiques peuvent être classées
en deux grandes catégories : les algorithmes à trajectoire et les
algorithmes à base de population.
Les algorithmes à trajectoire, aussi appelés
algorithmes à solution unique (Single-Solution Based) proposent
une seule solution et la modifient afin de la faire déplacer dans
l'espace de recherche, tandis que les algorithmes basés sur une
population (Population Based) maintiennent un groupe de solutions
potentielles et les font évoluer itérativement, puis
sélectionnent la meilleure.
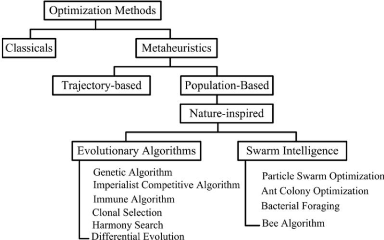
FIGURE 2.1 - Classification des
métaheuristiques [28]
2.3.1 Les méthodes à base de trajectoires
Ce type de méthodes se concentre sur
l'amélioration d'une solution en la faisant déplacer dans
l'espace de recherche formant ainsi une trajectoire.
Les trajectoires qui améliorent la solution seront
automatiquement acceptées, tandis qu'une trajectoire qui
décroît la qualité de la solution n'est pas
forcément refusée.
52
| 


