6. c.3. Evaluation de la qualité
des données sur les variables à utiliser
Tableau 2.2 : Récapitulatif des
observations sur les variables du modèle
|
Variables de l'étude
|
Effectif concerné
|
Effectif
non-concerné
|
Effectif enquêté
|
Taux de non réponse
|
|
Age de la femme
|
6896
|
0
|
6896
|
0,0
|
|
Milieu de résidence
|
6896
|
0
|
6896
|
0,0
|
|
Région de résidence
|
6896
|
0
|
6896
|
0,0
|
|
Taille du ménage
|
6896
|
0
|
6896
|
0,0
|
|
Condition de vie du ménage
|
6896
|
0
|
6896
|
0,0
|
|
Milieu de socialisation
|
6896
|
0
|
6860
|
0,6
|
|
Religion de la mère
|
6896
|
0
|
6855
|
0,6
|
|
Niveau d'instruction de la mère
|
6896
|
0
|
6896
|
0,0
|
|
Niveau d'instruction du conjoint
|
6635
|
261
|
6618
|
0,3
|
|
Activité économique de la mère
|
6896
|
0
|
6890
|
0,1
|
|
Activité économique du conjoint
|
6635
|
261
|
6616
|
0,3
|
|
Pratique contraceptive
|
6896
|
0
|
6896
|
0,0
|
|
IIP
|
5577
|
1319
|
5577
|
0,0
|
|
Rang de la naissance
|
6896
|
0
|
6896
|
0,0
|
|
Age à l'accouchement
|
6896
|
0
|
6896
|
0,0
|
|
Nombre de visites prénatales
|
6896
|
0
|
6896
|
0,0
|
|
Lieu d'accouchement
|
6896
|
0
|
6873
|
0,0
|
|
Assistance à l'accouchement
|
6896
|
0
|
6896
|
0,0
|
|
Taille à la naissance
|
6896
|
0
|
6883
|
0,2
|
|
Vaccination (Polio 0 et BCG)
|
6896
|
0
|
6896
|
0,0
|
|
Survie de l'enfant
|
6896
|
0
|
6896
|
0,0
|
NB : Lors des analyses,
sera créer une modalité résiduelle pour chaque variable
ayant fait l'objet d'un filtre (c'est-à-dire ayant des
non-concernés) afin de conserver la même taille de
l'échantillon.
d. Conclusion sur
l'évaluation de la qualité des données
Dans toute opération de collecte on enregistre toujours
des erreurs et des biais dû soit aux mauvaises déclarations
(observations) ou aux techniques de collectes utilisées. L'EDSR-III non
plus n'a pas échappée à cette réalité.
Cependant, les analyses précédentes faites sur la qualité
de ses données montrent que ces erreurs ne sont pas de nature à
compromettre les résultats des analyses futures. Ainsi, sans être
parfaites, les données issues de l'EDSR-III sont de qualité
acceptable.
La prise en compte du contexte (espace et temps) de
l'étude peut aider à comprendre certains résultats.
S'agissant des erreurs liées à la déclaration de
l'âge, plusieurs méthodes de lissage sont disponibles pour y
remédier (méthodes de Carrier et Farrag; Arriaga ; etc.). De
même, de nombreuses méthodes indirectes (P/F de Brass,
modèle de Gompertz, tables types de mortalité, etc.) permettent
d'ajuster les niveaux et les structures que ça soit pour la
fécondité ou la mortalité en cas de mauvaise
qualité des données. Cependant, dans le cadre de ce travail, ces
techniques ne seront ni développées, ni utilisées.
Malgré les quelques insuffisances soulignées ici et là,
les données seront finalement analysées sans aucun ajustement.
L'évaluation de leur qualité nous a permis de déceler
certaines limites que l'on prendra en compte, en cas de
nécessité, lors de l'interprétation des résultats
de nos analyses.
Après avoir présenté et
évalué la qualité des données à utiliser,
nous allons entrer dans les analyses proprement dites. Ces analyses auront pour
objectif de vérifier empiriquement les hypothèses de cette
étude. Les résultats obtenus vont permettre de formuler, par la
suite, des suggestions que se soient au niveau de la perspective de recherche
ou au niveau des stratégies à mettre en oeuvre en matière
de santé. Pour cela, il nous faut d'abord construire le fichier
d'analyse et choisir les méthodes d'analyse à utiliser.
e. Construction du fichier
d'analyse
Afin de pouvoir mener à bien nos analyses et obtenir
des résultats fiables, il nous est indispensable de construire un sous
fichier d'analyse de données contenant toutes les informations dont
nous avons besoin pour tester nos hypothèses et atteindre les objectifs
de l'étude. Rappelons que l'un des objectifs de cette étude est
d'évaluer la contribution de la planification familiale des femmes dans
l'amélioration de la survie des enfants de moins d'un an au Rwanda. La
population en observation est donc l'ensemble des enfants de moins d'un an. Or,
comme évoqué dans le paragraphe concerne d'effet de troncature,
la plupart des informations recueillies lors de l'enquête
démographique et de santé du Rwanda 2005 pour étudier la
mortalité des enfants portait sur les événements des cinq
dernières années qui ont précédé
l'enquête. La prise en compte de ce groupe quinquennal nous permet
d'éviter les effets de troncature.
Concrètement, à partir du fichier femme de la
base de données de l'EDSR-III renfermant les informations sur les femmes
et leur histoire génésique, nous extrayons toutes les
informations concernant l'étude, c'est-à-dire, les variables
contextuelles, les caractéristiques des ménages et des parents,
les comportements des mères vis - à - vis de leurs enfants telle
que les visites prénatales, la vaccination,..., les comportements
procréateurs, l'utilisation de la contraception et les
caractéristiques de l'enfant.
- L'âge à l'accouchement a été
construit à partir des dates de naissance de la mère et de
l'enfant saisies en CMC selon la relation suivante : âge de la
mère à l'accouchement (en années révolues)=
partie entière de {[date de naissance de l'enfant (en CMC) -
date de naissance de la mère (en CMC)]/12} ou grâce
à SPSS en prenant la valeur de {[date de naissance de
l'enfant (en CMC) - date de naissance de la mère (en CMC)]/12 -
0,5} arrondi à l'entier le plus
proche.
- La variable dépendante « survie
infantile (S.I) » a été créée
à partir de l'âge de l'enfant au décès (variable B7)
de la façon suivante :
S.I =1 si B7<12 et S.I = 0 sinon.
Construction de l'indicateur condition de vie du
ménage
L'indicateur condition de vie a
été construit en recourant à l'AFCM (Analyse factoriel de
classifications multiples) à l'aide du logiciel SPADV55. Les variables
utilisées dans la construction de cet indicateur sont :
ü l'approvisionnement en eau potable ;
ü le type de toilette ;
ü Type de matériaux du sol ;
ü la possession de l'électricité ;
ü le réfrigérateur ;
ü la possession d'une télévision ;
ü la possession d'une automobile ;
ü la possession d'un téléphone ;
ü la possession d'un vélo ;
ü la possession d'une radio ;
ü la possession d'un
réfrigérateur ;
ü la possession d'une moto/scooter.
Cette méthode nous a permis de distinguer 3
modalités :
ü Condition de vie faible : ce groupe
est composé, en moyenne, de ménages ne possédant ni radio,
ni télévision, ni téléphone, ni
réfrigérateur, ni électricité, ni vélo, ni
moto/scooter, ni voiture, utilisant des toilettes sommaires, ayant des maisons
construisent en sable ou en terre et s'approvisionnant en eau de surface ou
dans un puit. On peut dire que ces sont des ménages pauvres.
ü Condition de vie moyenne : ce
groupe est composé, en moyenne, de ménages ne possédant ni
télévision, ni électricité, ni
réfrigérateur, ni voiture. Ils possèdent par contre des
radios et des vélos, une toilette aménagée, des maisons en
ciment et s'approvisionnant en eau de robinet extérieur. Ce groupe est
susceptible d'avoir un niveau de vie moyen vu les conditions de vie des
ménages qui le composent.
ü Condition de vie
élevée : ce groupe est composé, en moyenne,
de ménages possédant un télévision et ayant
l'électricité comme mode d'éclairage, utilisant des
toilettes aménagées, s'approvisionnant en eau de robinet
intérieur et habitat dans des maisons en ciment. Ce groupe est
visiblement celui des ménages riches.
NB : La distribution statistique
des variables entrant dans la construction de cette indicateur sera
donnée en annexe.
Remarquons enfin que les informations concernant les enfants
décédés qui n'avaient pas été saisies au
moment de l'enquête sur les variables comme la vaccination, nombres de
visites prénatales,... ne causent plus de problèmes du faite que
ces variables ont été remplacées par les comportements des
mères malgré les conséquences évoquées
ci-haut.
f. METHODES D'ANALYSE DES
DONNEES
L'analyse des données est une démarche qui nous
permet de mesurer les effets et les mécanismes d'action de la
planification familiale des femmes appréhender à travers la
pratique contraceptive moderne sur la survie infantile au Rwanda. Dans cette
étude, trois niveaux d'analyses seront retenu: l'analyse
univariée, l'analyse bivariée et l'analyse multuvariée.
f.1. Analyse
univariée
Cette analyse permet de donner la distribution statistique
d'une variable pour déterminer le poids de chacune de ses
modalités, le taux de non-réponse, les non-concernés, les
valeurs manquantes et/ou les valeurs aberrantes mais aussi la manière
dont les valeurs sont dispersées par rapport à la moyenne, les
caractéristiques de tendances centrales et la forme de la courbe de
distribution (pour les variables quantitatives). C'est une analyse
essentiellement descriptive qui ne vise pas à rendre compte des
relations entre variables mais peut constituer une étape
préliminaire pour une analyse plus poussée. Elle fait partie de
l'étape de contrôle de la phase d'abstraction et permet enfin de
recoder certaines modalités, de tester l'hypothèse de
normalité, etc. (Anderson, 2001).
Dans cette étude, elle sera utilisée en vue du
recodage des variables, de la mesure des taux de réponse et des
non-concernés.
f.2. Analyse
bivariée
Ce niveau d'analyse permet d'étudier l'association
entre les variables explicatives et la survie infantile à l'aide des
tableaux croisées et du statistique du Khi deux.
En effet, notre variable dépendante étant
qualitative dichotomique (survie infantile ou décès infantile) et
les variables indépendantes qualitatives ou catégorielles, cette
statistique est la mieux indiquée pour rendre compte de l'association
entre ces variables. L'interprétation se fera à l'aide de la
probabilité associée au Khi-deux. Ce niveau d'analyse sert aussi
à connaître les différentielles de survie infantile entre
les différentes modalités de la variable indépendante
utilisée. Cependant, comme l'a bien dit Emile DURKHEIM :
«lorsque deux faits sociaux sont en relation et qu'on pense que
l'un est la cause de l'autre, il faut se demander si cette association ne
serait pas due à quelque cause de
cachée» (Legrand, 2008), les
relations observées au niveau bivarié peuvent être
fallacieuses du faite que ces observations sont faites toutes choses
n'étant pas égales. En d'autres termes, elles ne tiennent pas
compte des effets des autres variables en présence susceptibles de les
influencer. Ainsi, est-il indispensable de recourir à une analyse
multivariée afin de contrôler l'influence cachée de ces
variables pour pouvoir évaluer les effets nets des variables
analysées et confirmer ou d'infirmer les résultats
observés au niveau bivarié.
f.3. Analyse
multivariée
L'analyse multivariée s'attache à résumer
les données issues de plusieurs variables en minimisant la
déperdition de l'information. Elle recouvre un ensemble de
méthodes destinées à synthétiser l'information
issue de plusieurs variables, pour mieux l'expliquer (Taffé, 2004).
L'utilisation des différentes méthodes dépend de la nature
des variables (variables qualitatives ou quantitatives).
Dans notre étude, nous ferons recours à la
méthode de Régression Logistique Binomiale. Le
choix de cette méthode vient du fait que nous sommes en présence
d'une variable dépendante qualitative dichotomique et des variables
indépendantes qui, elles aussi sont qualitatives ou
catégorielles. Les résultats présentés par cette
méthode cadre bien avec l'objectif poursuivi par cette étude car
elle fournie les effets nets (rapport de côtes) de chaque variable
indépendante.
f.4.1. Le principe de
la méthode est le suivant :
La régression est une méthode à
partir de laquelle on cherche à faire passer une courbe
mathématique par un ensemble de points expérimentaux afin
d'appréhender l'évolution du phénomène
étudié (Leblanc, 2000 ; Essafi, 2003 cité par
Taffé, 2004). L'évolution de la variable observée peut
être expliquée à partir d'un ensemble de variables (les
variables explicatives). Cette méthode vise donc à trouver la
courbe passant au mieux par tous les points mesurés, soit en minimisant
l'erreur (la distance entre courbe théorique et points
expérimentaux).
La régression permet d'une part d'analyser dans quelle
proportion les variables explicatives concourent à la formation de la
variable d'intérêt ; d'autre part, le modèle ainsi
réalisé peut être utilisé à des fins
prédictives.
La régression linéaire dite « classique
» cherche à faire passer la « meilleure » droite par un
ensemble de points en minimisant l'erreur au sens des moindres carrés ;
dans ce cas le modèle est l'équation d'une droite, soit Y =
aX+b+å où Y représente la variable expliquée et X le
vecteur de mesure (a et b sont les coefficients, å représente le
résidu, ou l'erreur). Ainsi la mise en oeuvre de la régression
linéaire sous tend donc que la variable d'intérêt Y soit de
nature numérique car il semble difficile de borner le domaine de
variation d'un domaine classique aux valeurs [0,1] reflétant une
probabilité et donc une variable traduisant l'appartenance ou non
à une catégorie. La variable d'intérêt doit
être continue et les variables explicatives, quantitatives ou binaires.
De plus les variables utilisées doivent vérifier la condition de
normalité de la distribution et ne pas être fortement
inter-corrélées (condition de multi-colinéarité)
(Box, 1966 cité par Legrand, 2008).
Dans le cas où la variable expliquée est
qualitative, la régression logistique permet d'étudier l'effet
des variables explicatives de nature qualitative et quantitative. La nature
exacte de la variable d'intérêt (binaire, ordinale, nominale), va
donc imposer l'utilisation de régressions logistiques binaire,
ordonnée, polytonale ou encore conditionnelle (Thomas, 2000 cité
par Taffé 2004). Pour une variable dépendante binaire, une
régression logistique « classique » peut être mise en
oeuvre. Si la variable à expliquer comporte plus de deux
modalités, il faudra alors avoir recours à une régression
logistique multinomiale.
En tant que procédure non paramétrique, la
régression logistique présente l'avantage de « ne
pas exiger de contraintes quant à la normalité »
des distributions des variables. Les variables explicatives ne sont pas
forcément de nature continue et le lien entre variable
expliquée et explicatives n'est pas forcément
linéaire. La régression logistique est moins une
méthode d'inférence statistique qu'une méthode de
classification; en effet, l'équation étudiée traduit la
probabilité d'appartenance d'un individu a une catégorie ou un
groupe (Sheskin, 2007 cité par Taffé 2004). Ainsi, contrairement
à la régression traditionnelle (linéaire), les variables
expliquées peuvent être de nature quantitative et/ou qualitative.
Soit Y une variable binaire (oui/non par exemple). Soit X une
variable indépendante concourant à l'explication de Y. Y peut
prendre la valeur 1 avec la probabilité P(Y=1/X) et la valeur 0
avec la probabilité (1-P(Y=1/X)). Le modèle s'exprime
alors comme :
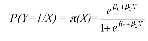
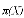 traduisant une probabilité, sa valeur doit être comprise
dans l'intervalle [0,1]. traduisant une probabilité, sa valeur doit être comprise
dans l'intervalle [0,1].
Soit la fonction logit définie par : g (p) =
ln (P/1-P)
Graphique 2.8 : Fonction Logit
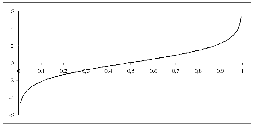
Source : Legrand, 2008
Si on applique la fonction logit à  , l'expression devient : , l'expression devient :
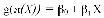
Le domaine de variation de  est compris entre est compris entre 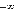 et et 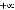 ., alors que ., alors que 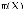 varie entre 0 et 1 ; une régression peut donc être mise en
oeuvre. L'estimation des paramètres varie entre 0 et 1 ; une régression peut donc être mise en
oeuvre. L'estimation des paramètres  et et 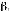 est faite par la méthode du maximum de vraisemblance. est faite par la méthode du maximum de vraisemblance.
Dans le cas où plusieurs variables (x1,x2, ..., xn)
explicatives sont intégrées à la régression, le
modèle s'exprime alors comme étant :

Pour calculer les coefficients de la régression
logistique, il suffit de prendre le logarithme du rapport des
probabilités :  Ces coefficients sont estimés par la méthode du maximum
de vraisemblance. Le rapport des probabilités est appelé «
Odds» (côte). On définit l'Odd comme étant le rapport
: Ces coefficients sont estimés par la méthode du maximum
de vraisemblance. Le rapport des probabilités est appelé «
Odds» (côte). On définit l'Odd comme étant le rapport
:
Odd = P/1-P
Où p traduit, par exemple, la
probabilité de réussir une action et 1- p, la
probabilité d'échouer. Il est important de noter que les
coefficients de la régression logistique ne présente pas les
odds mais les odds ratio (OR). Ces derniers traduisent les
chances que la variable y prenne la modalité j versus
la modalité de référence y=0, lorsque x=mod1,
versus x=mod2. Si on note p0 la probabilité de
réussir cette action pour une femme et p1 la probabilité de
réussir cette même action pour un homme, alors l'OR associé
au genre est égal au rapport :
Odd Ratio= (P1/1-P1)/
(P0/1-P0)
Si l'OR prend la valeur 1, cela traduit le fait que la
probabilité de réussir l'action est la même pour les hommes
que pour les femmes. Une valeur supérieure à 1 indique par contre
que les hommes ont plus de chance de réussir l'action que les femmes.
Dans le modèle logistique, les coefficients
calculés sont en fait égaux au logarithme népérien
de l'OR. Il faut donc appliquer la fonction exponentielle aux coefficients de
la régression afin de pouvoir analyser les Odds Ratio.
f.4.2. Interprétation des résultats
La plupart des logiciels offrent deux types de
résultats, les coefficients des X ou les odds ratio qui y sont
associés.
L'interprétation par les coefficients est
difficile :
Un coefficient négatif signifie que le Log odds (Ln?)
décroît d'une proportion équivalente au coefficient pour
tout accroissement unitaire de la variable indépendante. Le
résultat observé concerne alors la variation du Log de odds en
fonction de la variation de X et non la variation de la probabilité. Il
est donc difficile de l'interpréter directement.
L'interprétation par les odds ratio est
plus instructive :
Si â est négatif ; eâ
< 1 : on a moins de chance de vérifier la
propriété. Les individus appartenant à la modalité
considérée de la variable indépendante ont donc (1-
eâ) moins de chance de subir l'événement
étudié.
Si â = 0 ; eâ = 1 : pas de relation
entre X et Y.
Si â est positif, eâ > 1 : on a
plus de chance de vérifier la propriété. Les individus
appartenant à la modalité considérée de la variable
indépendante ont donc (eâ -1) plus de chances de subir
l'événement étudié ou eâ fois
plus de chance de subir le événement étudié.
Où â représente la valeur du coefficient de X dans
l'équation du modèle (Rwenge, 2008).
f.4.3. Adéquation
du modèle
La statistique du khi-deux sert à s'assurer de
l'efficacité globale du modèle. Elle permet de rejeter ou non
l'hypothèse selon laquelle tous les coefficients dans le modèle
sont nuls. Elle sert donc de test d'adéquation du modèle à
prédire le phénomène étudié.
Ce test d'adéquation du modèle est fait à
partir de la probabilité associée à cette statistique du
khi-deux. Si cette probabilité est inférieure au seuil choisi, le
modèle est adéquat. Ceci signifie que les variables
indépendantes considérées dans l'ensemble expliquent la
variation de la variable dépendante. Elles peuvent donc prédire
la valeur de Y. Dans cette étude nous estimerons que le modèle
est adéquat lorsque la probabilité associée au khi-deux
est inférieure ou égale à 5%.
Evaluation du pouvoir discriminant du
modèle : sensibilité, spécificité et courbe ROC
(Taffé, 2004)
On utilise le modèle Logistique pour modéliser
la probabilité des attributs 0/1 de la variable dépendante y
en fonction des co-variables x1, x2, ..., xp. A
partir des probabilités estimées on décide en fixant un
seuil, par exemple à 5%, de classer l'individu dans la catégorie
y = 1 si sa probabilité est supérieure au seuil et dans
la catégorie y = 0 sinon. Il est donc intéressant de
déterminer la performance du classement et comme celui-ci dépend
du seuil (ou de la règle) choisi, nous allons considérer les
notions de sensibilité et spécificité.
La sensibilité est définie comme la
probabilité de classer l'individu dans la catégorie y =
1 (on dit que le test est positif) étant donné qu'il est
effectivement observé dans celle-ci, c'est -à- la capacité
de prédire un événement :
Sensibilité = Prob (test + | y = 1)
La spécificité est définie comme la
probabilité de classer l'individu dans la catégorie y =
0 (on dit que le test est négatif) étant donné qu'il est
effectivement observé dans celle-ci, c'est -à- la capacité
à prédire un non-événement :
Spécificité = Prob (test - | y = 0)
Graphique 2.9 : Courbe de
sensibilité-spécificité

Source : P. Taffé, cours
de égression logistique, Lausanne 2004
Comme indicateur de la capacité du modèle
à discriminer nous utiliserons la courbe ROC
(Receiver Operating Characteristic). L'aire sous cette courbe est une mesure du
pouvoir prédictif de la variable X.
Nous retiendrons ainsi comme règle du pouce :
Si aire ROC = 0.5 il n'y a pas de discrimination ;
Si aire 0.7 <= ROC ?< 0.8 la discrimination est
acceptable ;
Si aire 0.8 <= ?ROC ?<0.9 la discrimination est
excellente ;
Si aire ROC >= ?0.9 la discrimination est
exceptionnelle.
Cependant, le pseudo R2 en est aussi un indicateur
du pouvoir prédictif du modèle mais l'interprétation de
cette dernière peut conduire à des résultats
biaisés du fait que l'appréciation de sa grandeur dépend
de l'expérience de l'utilisateur. En d'autres termes, il n'y a pas de
règle de décision permettant de conclure si le modèle est
bon ou pas. Ainsi, nos interprétations se feront grâce à la
courbe ROC.
Pour ce qui concerne la présentation des
résultats d'analyse aussi bien au niveau bivarié que
multivarié, les conventions suivantes seront adoptées :
ü Trois astérisques (***) pour les
paramètres significatifs à un seuil de 1% ;
ü Deux astérisques (**) pour les paramètres
significatifs au seuil de 5 % ;
ü Un astérisque (*) pour les paramètres
significatifs au seuil de 10 % ;
ü Le symbole «ns», pour les paramètres
non significatives ;
ü Le symbole « ® » servira
à l'identification de la modalité de référence pour
les modèles de régression logistique.
Ces méthodes statistiques ainsi
présentées nous permettront de vérifier nos
hypothèses et de répondre à la question de l'étude.
La constitution du fichier d'analyse permettra dans les chapitres suivants
l'utilisation de ces méthodes d'analyse statistiques en vue de mettre en
évidence des effets de la planification familiale des femmes sur la
survie des enfants de moins d'un an au Rwanda et les mécanismes
d'action.
| 


