|
5. Survie Infantile
Niveau ménage
- Milieu de socialisation de la mère
- Religion de la mère
- Niveau d'instruction de la mère
- Niveau d'instruction du conjoint
- Activité économique de la mère
- Activité économique du conjoint
Niveau individuel
- Condition de vie
- Taille du ménage
- Milieu de résidence
- Région de résidence
Niveau contextuel
eur
Facteurs comportementaux
Utilisation des méthodes contraceptives moderne
- Nombre de visites prénatales
- Lieu d'accouchement
- Assistance à l'accouchement
- Taille de l'enfant à la naissance
- Vaccination
- Age au sevrage partiel
- Intervalle intergénésique
précédent
- Age de la mère à l'accouchement
- Rang de la naissance
2.4 METHODOLOGIE DE L'ETUDE
Tout
travail scientifique cherche à tester les hypothèses
émises dans cette recherche afin d'atteindre les objectifs fixés
au départ. Il doit donc s'appuyer sur des données réelles
de qualité et des méthodes d'analyses bien
élaborées qui sont un préalable à celui-ci.
Ainsi,
ce chapitre traite de la source et de l'évaluation de la qualité
des données, de la construction du fichier d'analyse, et des
méthodes et modèles d'analyses utilisés.
a. Sources de
données utilisées
Pour tester nos hypothèses d'étude, nous
utiliserons les données de l'Enquête Démographique et de
Santé du Rwanda (EDSR-III) réalisée en 2005. Cette
enquête est la troisième du genre après celles
menées successivement en 1992 et 2000. Elle visait la population des
individus qui résidaient dans les ménages ordinaires à
travers tout le pays. Elle a été réalisée sur un
échantillon représentatif de femmes de 15-49 ans et d'hommes de
15-59 ans (cependant, notre étude portera uniquement sur l'enquête
femme).
La méthode d'enquête utilisée est un
sondage par grappes stratifiée à deux degrés. La base de
sondage est la liste des zones de dénombrement (ZD) du Recensement
Général de la Population et de l'Habitat de 2002 (RGPH-2002),
préparé par le Service National de Recensement. A cause de la
répartition non proportionnelle de l'échantillon parmi les
strates, et du fait qu'on a fixé le nombre de ménages dans chaque
grappe, des taux de pondération ont été utilisés
pour assurer la représentativité actuelle de l'échantillon
au niveau national et au niveau régional.
Au total, 10 644 ménages ont été
sélectionnés pour l'EDSR-III et, parmi eux, 10.307 ménages
ont été identifiés au moment de l'enquête, soit
96,8% de ménages sélectionnés. Parmi ces 10.307
ménages, 10.272 ont pu être enquêtés avec
succès, soit un taux de réponse de 99,7 %. A l'intérieur
des 10.272 ménages enquêtés, 11.539 femmes
âgées de 15-49 ans ont été identifiées comme
étant éligibles pour l'enquête individuelle, et pour 11.321
d'entre elles, l'interview a pu être menée à bien. Le taux
de réponse s'établit donc à 98,1 % pour les interviews
auprès des femmes.
a.1.
Questionnaires
Trois questionnaires ont été utilisés au
cours de l'EDSR-III : le Questionnaire Ménage, le Questionnaire Femme et
le Questionnaire Homme (les deux premiers nous concernent dans cette
étude).
Le Questionnaire Ménage a été
utilisé pour lister tous les membres habituels et les visiteurs des
ménages sélectionnés. Des informations de base sur les
caractéristiques de chaque personne ont été
collectées, y compris l'âge, le sexe, l'éducation et le
lien avec le chef de ménage. L'objectif principal de ce Questionnaire
était d'identifier les femmes et les hommes éligibles pour des
interviews individuelles. Il a aussi permis de collecter des informations sur
les caractéristiques du ménage.
Le Questionnaire Femme a été utilisé pour
collecter des informations sur toutes les femmes en âge de
procréer (15-49 ans). Ces informations concernaient entre autres,
l'histoire génésique, les comportements en matière de
santé de la reproduction, de nutrition de l'enfant, ...
xviii. a.2. Objectif de l'EDSR-III
L'EDSR-III avait plusieurs objectifs principaux entre autres
:
- Recueillir des données à l'échelle
nationale qui permettent de calculer des taux démographiques essentiels,
plus particulièrement les taux de fécondité et de
mortalité infantile et infanto juvénile et d'analyser les
facteurs directs et indirects qui déterminent le niveau et la tendance
de la fécondité et de la mortalité infanto
juvénile ;
- Mesurer les niveaux de connaissance et de pratique
contraceptive des femmes et des hommes;
- Recueillir des données sur la santé
familiale : vaccination, prévalence et traitement de la
diarrhée, des Infections des Voies Respiratoires Aiguës (IRA) et
de la fièvre et/ou de convulsions chez les enfants de moins de cinq
ans, visites prénatales et assistance à l'accouchement ;
- Recueillir des données sur les pratiques
nutritionnelles des enfants, y compris l'allaitement, et dans la moitié
des ménages échantillonnés, prendre des mesures
anthropométriques pour évaluer l'état nutritionnel des
femmes et des enfants, et réaliser un test d'anémie auprès
des enfants de moins de cinq ans, des femmes de 15-49 ans et des hommes de
15-59 ans ;
b. Limites
méthodologiques et évaluation de la qualité des
données de l'EDSR-III
Les résultats des enquêtes sont
tributaires de la qualité des données. Une première
tâche à laquelle on doit s'atteler avant d'effectuer une
quelconque analyse consiste donc à  évaluer la qualité des données à utiliser.
Ceci permet de connaître les biais pouvant exister et les limites de
l'étude. évaluer la qualité des données à utiliser.
Ceci permet de connaître les biais pouvant exister et les limites de
l'étude.
b.1. Biais de
sélection
Comme toutes les enquêtes rétrospectives, seules
les femmes survivantes ayant passé la nuit précédent le
passage de l'agent enquêteur dans les ménages ont
été enquêtées. Les femmes
décédées ou celles n'ayant pas passé la nuit de
référence dans leurs ménages sont ainsi exclues de
l'échantillon. Ceci entraîne un biais de sélection du fait
que les enfants dont les mères sont décédées sont
susceptibles d'avoir un risque de mortalité élevé que les
autres alors qu'ils ont été exclus de l'échantillon. De
plus, n'ayant aucune idée sur la durée ou le motif d'absence des
mères qui n'ont pas passés la nuit de référence
dans leurs ménages, il pratiquement impossible de contrôler les
effets de celle-ci sur la survie de leurs enfants. Ainsi, on est conduit
à émettre l'hypothèse de non sélection pour les
femmes enquêtées qui suppose que l'échantillon choisit est
représentatif de la population cible. En d'autres termes, elle stipule
que les mères décédées ou absentes auraient eu les
mêmes comportements que ceux observés chez les mères
enquêtées et que donc les enfants orphelins ou dont les
mères sont absentes seraient soumises aux mêmes risques de
mortalité que ceux des mères enquêtées. Cette
hypothèse est peu réaliste dans le contexte africain où la
mère reste irremplaçable pour
la santé de son enfant. De plus, les mères
décédées étaient probablement les moins robustes
que celles qui sont encore en vie. Ce qui pouvait augmenter les risques de
mortalité chez leurs enfants. De même pour les mères
absentes à cause de longues maladies, surtout si celles-ci souffraient
pendant la grossesse ou même lors de la période infantile.
Nous supposons aussi qu'il n'y a pas d'effet sélection
pour les enfants observés parmi tous les enfants nés vivants
d'une femme enquêtée. En d'autres termes, nous supposons que les
mères ont eu les mêmes comportements tant pour les enfants
décédés que pour les survivants. Ce qui est
invraisemblable du fait qu'une mère peut être amenée
à changer de comportements suivant les expériences vécues
des précédentes naissances ou des événements
survenus à celles-ci. De plus, le fait que ces enfants soient
décédés et non les autres peut être dû
effectivement à ces comportements différentiels des mères.
Cette démarche pose un problème. En effet, il est impossible
d'associer les variables relative aux comportements de la mère en
matière de santé à un enfant décédé
si sa mère n'a eu que lui seul au cours de la période retenue
pour l'enquête ou si les autres enfants nés avant ou après
lui au cours de la période de l'enquête sont aussi
décédés.
b.2. Biais
d'observation
Lorsqu'on cherche à expliquer la mortalité des
enfants par les caractéristiques et comportements de leurs mères,
comme la pratique contraceptive moderne, les enquêtes EDS
présentent une autre limite : il existe souvent un décalage entre
les caractéristiques et comportements de la mère au moment de
l'enquête et au moment du décès de l'enfant. La mère
peut avoir eu recours à la pratique contraceptive moderne après
la naissance ou même le décès de son enfant,
peut-être même pour éviter que ne se reproduise un
problème constaté sur l'enfant décédé. Tout
de même, les enquêtes biographiques permettraient de surmonter un
tel inconvénient. Ainsi, les résultats peuvent conduire à
des conclusions mitigées lorsque l'écart est important.
b.3. Effet de
troncature
Le caractère rétrospectif des renseignements
recueillis lors des EDS entraîne un autre problème
méthodologique qu'est la
« troncature » lorsque l'on
s'intéresse à la mortalité des enfants sur une
période de 5 ans avant la date de l'enquête. En effet, tous les
enfants n'ont pas été exposés au risque de
décéder pendant une même durée. Les
générations les plus récentes comme celle d'enfants
nés l'année qui précède l'enquête ne l'ont
été que pendant 0,5 an en moyenne (sous l'hypothèse
d'uniforme répartition des naissances durant ces douze derniers mois) :
C'est l'effet de troncature. Il est alors
nécessaire de délimiter une période d'analyse dans
laquelle tous les enfants ont été soumis au risque de
connaître l'événement
« décès » pendant la même durée.
Cette exigence est satisfaite comme le montre la Graphique 2.1
qui explicite la délimitation des quatre
générations d'enfants sur lesquelles porte l'étude.
Graphique 2.1 : Diagramme de Lexis pour
les cinq dernières générations précédent
l'enquête

Où t représente à la
date exacte de l'enquête.
En particulier, pour l'étude de la survie infantile,
les enfants concernés doivent avoir été exposés aux
risques de décès infantile durant une année (pour ceux qui
sont encore en vie) ou l'auraient été s'ils n'étaient pas
décédés. Ainsi, sommes-nous obligés d'exclure la
dernière génération de notre analyse, c'est -à-
dire celle des enfants nés au cours de la période annuelle
[t-1, t], puisqu'elle ne satisfait pas
à cette condition. En effet, rien ne permet de dire qu'un enfant
survivant de cette génération atteindra ou non son premier
anniversaire.
Compte tenu de ce problème et du faible effectif de
décès qu'on enregistrerait dans les générations
totalement exposées au risque de décéder si nous
considérons une période annuelle, [t-2, t-1]
uniquement par exemple, nos analyses porteront sur la cohorte d'enfants
nés au cours de la période [t-5, t-1],
c'est-à-dire les quatre dernières générations
précédent les douze mois avant de l'enquête.
b.4. Erreurs dues au choix
de l'échantillon
Les limites des enquêtes par sondage tiennent
essentiellement aux erreurs d'échantillonnage et aux difficultés
de désignation de l'échantillon. On distingue pour cela trois
sources d'erreurs : erreur d'échantillonnage, biais
d'échantillonnage, erreur indépendante de
l'échantillonnage. La première source d'erreur est le
degré de variation des réponses suivant l'échantillon. En
effet, l'échantillon constitué étant aléatoire, le
tirage aurait pu tomber sur un autre et les réponses enregistrées
auraient été au moins quelques peu différentes de celles
qui l'ont été effectivement. Cette erreur peut être
contrôlée par le dispositif de collecte. Des biais pourraient
être dus au plan de sondage utilisé (base de données
défectueuse, éléments manquants, méthode de tirage
de l'échantillon, etc.) et/ou à une mauvaise procédure
d'estimation. Enfin, indépendamment des problèmes liés
à l'échantillon, il existe des sources d'erreurs dues
principalement aux variations causées par les enquêteurs, les
opérations de codage, des erreurs de mesure, des données
manquantes, etc.
b.5. Biais relatifs
aux informations spécifiquement liées à la santé de
l'enfant
Certaines informations liées aux comportements
nutritionnels et sanitaires de la mère vis-à-vis de son enfant
(vaccination, visites prénatales, durée d'allaitement,...) n'ont
été posées que pour les enfants encore en vie au moment de
l'enquête. Ainsi, il pratiquement impossible d'utiliser ces informations
pour étudier l'influence de ces comportements sur les risques de
décès ou les chances de survie infantile. Pour pallier à
ce problème, nous sommes conduit à poser une hypothèse
forte considérant que les mères ont observées les
mêmes comportements pour ces enfants que ceux qui sont encore en vie.
Cependant, cette hypothèse n'est pas toujours vérifiée
puisque les comportements d'une mère peuvent varier suivant les
circonstances et le temps. Cela risque donc de sous estimer la mortalité
infantile du fait que les enfants décédés ont en moyenne
plus de chances d'avoir eu un comportement défavorable de la part de
leurs mères.
Une autre limite vient de la mauvaise qualité des
données sur les variables poids à la naissance et mesures
anthropométriques rendant compte de l'état sanitaire et
nutritionnel de l'enfant et de la mère pour lesquelles les valeurs
manquantes sont d'environ 70%. Ces facteurs sont en effet capital pour une
étude sur la survie infantile du faite qu'elles font partie des
déterminants proches de la mortalité infantile. Cela nous a
conduit à chercher des facteurs approximatifs comme la taille de
l'enfant à la naissance qui ne montre pas en réalité le
vrai poids puisque l'enquêteur devrait se contenter de la simple
déclaration de la mère estimant que son enfant était
né très petit, petit, moyen, grand ou très grand sans
donner aucune précision sur la vraie valeur de ce signifie ces termes.
Par ailleurs, les données dont nous disposons ne nous
permettent pas d'utiliser le facteur « allaitement »
malgré toute son importance pour rendre compte de l'état
nutritionnel de l'enfant. En effet, ce dernier peut être saisi, par ordre
d'importance, à travers : la durée d'allaitement,
l'âge au sevrage partiel, le type d'allaitement ou la consommation du
colostrum. Or, ces données ne permettent l'utilisation d'aucune de ces
variables :
L'utilisation de la variable « durée
d'allaitement » présente une limite liée à la
manière dont elle a été saisie. En effet, pour saisir
l'information concernant cette variable, l'enquêtée
répondait aux questions suivantes :
- « avez-vous allaité
(nom) ? »,
- Si oui, « allaitez-vous
encore ? », et au cas où elle
n'allaitait plus son enfant, « pendant combien de
mois avez-vous allaité (nom) ? » (uniquement
si l'enfant est en vie).
Ainsi, pour les enfants encore allaités, il est
difficile de connaître à priori le moment auquel leur mère
va arrêter l'allaitement, leur durée d'allaitement correspond
alors à leur âge actuel. En revanche, pour ceux qui sont
décédés, on peut se demander si c'est l'arrêt
précoce d'allaitement qui a provoqué le décès
(auquel cas l'allaitement serait un des facteurs explicatifs du
décès de l'enfant) ou bien au contraire si l'arrêt de
l'allaitement était dû au décès de l'enfant
(auquel cas la durée d'allaitement n'a rien à voir avec
le décès de l'enfant) (RAKOTONDRABE., 2004). A titre
d'exemple, un enfant qui décède un jour après sa naissance
aura tété au plus un jour. Pouvons-nous penser que c'est le fait
qu'il soit allaité uniquement un jour qu'il est
décédé ? ou que cela ait contribué à
cette mort ?
L'utilisation de cette variable peut dans ce cas introduire un
biais dans les résultats des analyses du fait que la durée
d'allaitement saisie par l'enquête ne correspond pas au moment de sevrage
de l'enfant. En effet, la durée moyenne d'allaitement (ou âge
moyen au sevrage total) pour les enfants décédés ne peut
pas dépasser un an du fait que les décès qui nous
concernent sont ceux des enfant de moins d'un an alors que la moyenne de
l'ensemble était d'environ 25 mois en 2005. Cela peut conduire à
des conclusions erronées affirmant que les enfants
décèdent parce que leurs mères observent un mauvais
comportement en refusant des les allaiter. Or, l'enquête n'a saisie
aucune information sur l'âge au sevrage de l'enfant (ni sur le sevrage
partiel, ni sur le sevrage total). De plus, le type d'allaitement n'est
même pas saisi alors que la consommation du colostrum ne l'a
été que pour la dernière naissance uniquement et ne peut
donc pas être utilisée dans notre étude puisque la prise en
compte de cette naissance uniquement surestimerait largement la survie
infantile. Ainsi, malgré toute l'importance de l'allaitement sur la
survie infantile, elle ne sera pas utilisée dans nos analyses.
c. Evaluation de la
qualité des données
c.1. Evaluation des
données sur l'âge des femmes
enquêtées
L'âge est l'une des variables les plus importante dans
l'analyse démographique. Cependant, cette variable est d'ordinaire
à la source d'erreurs de mémoire et d'autres types de biais
surtout dans le contexte de faible alphabétisation. Une mauvaise
déclaration de l'âge peut donc conduire à des analyses
détournées et à des conclusions fallacieuses. L'examen des
données sur l'âge des femmes déclaré à
l'enquête peut donner une idée sur la qualité de celles-ci.
Ainsi s'impose avant toute chose une évaluation de la qualité
des données sur l'âge déclaré des femmes.
L'échantillon étant aléatoire (aucun quota imposé
selon l'âge des femmes parmi celles éligibles), on s'attend
à ce que les effectifs des femmes décroissent avec l'augmentation
de l'âge à cause de la mortalité. Les femmes plus
âgées ayant été exposées à la
mortalité plus longtemps que leurs petites soeurs, leur effectif
devraient diminuer toutes choses égales par ailleurs.
Graphique 2.1: Répartition des
femmes enquêtées (en %) selon l'âge
déclaré.

La figure précédente n'indique aucune
préférence pour les âges ronds ou semi-ronds, ce qui laisse
penser à une bonne déclaration sur cette variable. Afin
d'approfondir un peu plus cette évaluation de la qualité des
données sur l'âge et en savoir plus sur une éventuelle
attraction ou répulsion, nous calculons ci-après les indices de
Whipple et de Myers.
c.1.1. Indice de Whipple
L'indice de Whipple (I w) permet
de mesurer le degré de préférence des âges se
terminant par 0 ou 5. Le calcul de cet indice consiste à prendre
l'effectif total des femmes âgées de 23 à 62 ans, calculer
la somme des effectifs des femmes de cet intervalle dont les âges se
terminent par les chiffres 0 ou 5, et faire le rapport de cette dernière
au un cinquième de l'effectif total. L'indice ainsi obtenu varie entre
zéro et cinq. Mais pour les données issues des EDS (Gendreau et
al, 1985), concernant uniquement les femmes de 15 ans à 49 ans, la
formule est la suivante :

Les valeurs proposées par les Nations Unies pour
apprécier la qualité des données sur l'âge à
partir de cet indice sont (Roger et al, 1981) :
ü Si I w = 0, il y a
répulsion total pour les âges se terminant par 0 et 5 ;
ü Si I w = 5, tous les
âges enregistrés se terminent par 0 ou 5 ;
ü Si I w < 1, il y a
répulsion pour les âges se terminant par 0 et 5 ;
ü Si I w = 1, il n'y a
préférence ni répulsion pour les âges terminant par
0 ou 5 ;
ü Si 1 < I w < 5, il y a
attraction d'autant plus forte que I w
est proche de 5.
Cependant, ces valeurs sont très théoriques,
ainsi, les Nations Unies propose la classification suivante relative à
l'Indice de Whipple (Roger et al, 1981) :
ü Si Indice de Whipple < 1,05 : les données
sont très exactes ;
ü Si 1,05 = Indice de Whipple = 1,099 : les
données sont relativement exactes ;
ü Si 1,10 = Indice de Whipple = 1,249 : les
données sont approximatives ;
ü Si 1,25 = Indice de Whipple = 1,749 : les
données sont grossières ;
ü Si Indice de Whipple = 1,75 : les données sont
très grossières.
Le calcul de l'indice de Whipple pour les données des
EDSR-III 2005 donne une valeur de I w =1,013. Cette
valeur est inférieur à 1,05 et suggère que les
données sont très exactes. Cela signifie en outre qu'il n'y a
aucune attraction ni répulsion pour les âges ronds et semi ronds.
On peut donc dire que les femmes enquêtées ont globalement bien
déclaré leurs âges. Cela confirme les observations faites
sur le graphique précédent. Cependant, l'indice de Whipple
présente certaines limites. Il ne permet de se prononcer que sur la
préférence aux âges se terminant par zéro ou cinq.
c.1.2. Indice de Myers
Contrairement à l'indice de Whipple, celui de Myers
mesure la répulsion ou l'attraction pour chacun des chiffres compris
entre zéro et neuf. Il permet aussi de se prononcer de façon
globale sur l'ensemble des chiffres. Cet indice présente aussi
l'avantage d'éliminer, au moins en partie, la diminution des chiffres
entre les âges en se servant des effectifs pondérés. Il
varie entre 0 et 180. Plus il est proche de zéro, meilleure est la
déclaration des âges. Pour chaque chiffre, le signe négatif
du coefficient indique une répulsion, tandis que le signe positif
traduit une attraction. La valeur absolue du coefficient renseigne sur
l'ampleur de la préférence (Gendreau, 1993). Elle sera chaque
fois comparée à 20 pour apprécier la force de cette
attraction ou répulsion aux âges se terminant par le chiffre
concerné alors que la valeur de l'indice sera comparé à 0
et à 180 pour apprécier la qualité globale des
données en rapport aux éventuelles préférences ou
répulsions.
Procédé de calcul
Etape 1 :
On calcul les sommes   des effectifs des personnes 10 ans et plus, dont les âges se
terminent respectivement par chacun des chiffres de 0 à 9. des effectifs des personnes 10 ans et plus, dont les âges se
terminent respectivement par chacun des chiffres de 0 à 9.
Soit P (10d+u), l'effectif des personnes dont l'âge a
pour chiffre des dizaines « d » et pour chiffre des
unités « u » :
  . .
Etape 2 :
On calcul de même les sommes   pour les 20 ans et plus : pour les 20 ans et plus :
 
Etape 3 :
Les effectifs remaniés de Myers sont les
quantités Tu définies par :
Tu = (u+1)  +(9-u) +(9-u)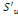 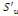
Etape 4 :
On calcul l'effectif remanié total T :
T=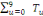 
Etape 5 :
L'indice de Myers vaut alors :
IM=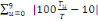 
Tableau 2. 1 : Indices de Myers EDSR-III
2005
|
u
|
Su
|
u+1
|
S'u
|
9-u
|
Tu
|
100Tu/T
|
100T/T-10
|
|100T/T-10|
|
|
0
|
1033
|
1
|
565
|
9
|
6121
|
8,328
|
-1,7
|
1,7
|
|
1
|
948
|
2
|
483
|
8
|
5763
|
7,840
|
-2,2
|
2,2
|
|
2
|
1045
|
3
|
540
|
7
|
6916
|
9,410
|
-0,6
|
0,6
|
|
3
|
1017
|
4
|
531
|
6
|
7254
|
9,868
|
-0,1
|
0,1
|
|
4
|
911
|
5
|
481
|
5
|
6959
|
9,468
|
-0,5
|
0,5
|
|
5
|
870
|
6
|
484
|
4
|
7158
|
9,738
|
-0,3
|
0,3
|
|
6
|
819
|
7
|
449
|
3
|
7081
|
9,634
|
-0,4
|
0,4
|
|
7
|
785
|
8
|
429
|
2
|
7139
|
9,712
|
-0,3
|
0,3
|
|
8
|
1013
|
9
|
493
|
1
|
9607
|
13,070
|
3,1
|
3,1
|
|
9
|
950
|
10
|
519
|
0
|
9504
|
12,930
|
2,9
|
2,9
|
|
TOTAL
|
|
|
|
|
73503
|
100
|
|
12,0
|
Le tableau précédent donne les écarts des
pourcentages de chacun des effectifs remaniés avec l'effectif
théorique 10. On remarque que ces écarts ne se pas
élevés, ce qui signifie qu'il n'y a pas de
préférence prononcée d'âge. La somme des valeurs
absolues de ces écarts donne l'indice de Myers qui est ici de
12. Cet indice confirme encore une fois l'absence de
préférence ou d'aversion d'une manière globale.
L'étude des écarts observés à chaque âge se
terminant par un chiffre de 0 à 9 montre des faibles attractions aux
âges se terminant par 8 et 9 et de faibles répulsions aux
âges 0 et 1. Cependant, ces écarts sont suffisamment faibles qu'on
ne peut pas affirmer qu'il y a eu préférence ou aversion à
ces âges. Ainsi, ces résultats nous laissent penser que les
données observées sur l'âge des femmes sont de bonne
qualité.
Néanmoins, le graphique 2.1 a
montré de petites irrégularités sur la courbe
représentative des effectifs des femmes enquêtées par
année d'âge déclaré au moment de l'enquête.
Pour corriger ces irrégularités, nous procédons à
un lissage de cette courbe en opérant des regroupements des femmes par
groupes quinquennaux. De même, on s'attend à ce que la courbe
représentant les effectifs des femmes enquêtées par groupes
d'âges quinquennaux soit monotone décroissante. En d'autres
termes, plus l'âge augmente, l'effectif femmes du groupe devrait
diminuer. Le graphique suivant représente les effectifs des femmes
enquêtées pas groupes d'âges quinquennaux.
Graphique 2.2 : Répartition (en %)
des femmes enquêtées par groupes d'âges quinquennaux.

L'examen de ce graphique montre effectivement une
décroissance régulière des effectifs des femmes à
mesure que l'âge augmente. Ainsi, nous pouvons confirmer encore une fois
que la qualité des données sur l'âge des femmes
enquêtées est bonne d'autant plus que nos analyses utiliseront les
données agrégées et non les données en année
d'âge.
c.2. Omission des
naissances et des décès
Dans les enquêtes rétrospectives, les femmes
oublient généralement certaines naissances,
particulièrement lorsque les enfants n'habitent plus avec elles ou
lorsque la naissance est suivie du décès de l'enfant à un
âge très jeune. L'omission des naissances ou des
décès peut donc être volontaire, surtout dans le contexte
africain (pour des raisons culturelles ou de superstition), ou due à une
défaillance de mémoire. En procédant à l'examen des
tendances internes observées (naissances et décès), on
peut avoir une idée sur l'importance de ces omissions. Ces tendances ne
doivent pas s'écarter beaucoup de l'ordinaire, dans le cas contraire,
cela traduirait une omission des naissances ou une hausse récente de la
mortalité après une baisse dans les périodes moins
récentes, ce qui peut être improbable (connaissant le contexte du
pays).
c.2.1. Nombre d'enfants
nés vivants
Dans un pays à fécondité naturelle, le
nombre moyen d'enfants par femme croît avec l'âge jusqu'à 49
ans. Ceci pourrait s'expliquer par le fait que la durée moyenne
d'exposition au risque de conception augmente avec l'âge jusqu'à
la ménopause. De ce fait, en l'absence d'une forte hausse de la
fécondité dans le temps, l'observation d'une baisse de la
parité moyenne lorsqu'on l'âge augmente ne peut alors s'expliquer
que par une omission d'enfants nés vivants ou un rajeunissement (ou
vieillissement) de certaines mères.
Graphique 2.3: Répartition du nombre
moyen d'enfants nés vivants selon le groupe d'âge
des femmes

Le graphique précédent montre globalement une
augmentation régulière de la parité moyenne selon
l'âge déclaré de la femme. Remarquons cependant de petites
perturbations aux âges 39 et 48 ans où la parité atteinte
chute spontanément en faveur des âges qui suivent.
Théoriquement, une diminution brusque de la parité s'expliquerait
soit par un vieillissement de certaines mères, des omissions d'enfants
ou un changement de la fécondité dans le temps. Pour le cas
présent, il est difficile de se prononcer puisque les attractions sont
souvent observées pour les âges ronds ou semi ronds et non sur 39
et 48 ans. De plus, il n'est pas aussi réaliste de penser que les
omissions ou le changement de la fécondité aient des effets
observables uniquement à 39 et 48 ans. Nous n'oublions pas aussi que la
taille de l'échantillon est un élément important dans la
précision des estimations, le fait observé peut donc être
dû à la non représentativité de l'échantillon
(quand les données sont désagrégées, la taille de
l'échantillon peut devenir insuffisant et l'échantillon non
représentatif à tous les âges) et non à une
mauvaise déclaration des âges. Ainsi, on peut estimer que les
naissances sont à peu près bien déclarées.
Pour essayer de remédier à ces petites rancunes
observées, on va procéder à un regroupement de femmes en
groupes quinquennaux. Ainsi, le graphique ci-après représente les
parités moyennes des femmes par groupes d'âge quinquennaux au
moment de l'enquête.
Graphique 2.4 : Parités moyennes
des femmes selon leurs groupes d'âges à l'enquête.

L'examen de cette courbe montre une croissance
régulière des parités moyennes en fonction de l'âge
de la femme au moment de l'enquête. Ainsi, on peut penser que, les
naissances ont été globalement bien déclarées ou
que si mauvaises déclarations il y a eu, elles n'ont pas
été trop importantes pour mettre en cause la qualité des
résultats des analyses sur les naissances vivantes.
c.2.2. Evaluation de la
qualité des données sur les enfants décédés
selon l'âge de la mère
Il est généralement observé à
partir des enquêtes présentant des résultats
cohérents, une corrélation positive régulière du
nombre moyen d'enfants décédés ou de la proportion
d'enfants décédés par femme et l'âge de celle-ci au
moment de l'enquête à partir du groupe d'âge 20-24 ans
(Gendreau, 1985). En effet, la durée moyenne d'exposition aux risques de
décéder est plus élevée pour les enfants nés
des femmes plus âgées au moment de l'enquête du fait que ces
enfants sont en moyenne plus âgés que ceux issus des femmes plus
jeunes.
Graphique 2.5 : proportion de
décès observés selon l'âge de la mère
à l'enquête

L'analyse du graphique précédent montre
globalement que le nombre d'enfants décédés par femme
croît avec l'âge de la femme au moment de l'enquête. On peut
alors dire que les omissions de décès ne sont pas importantes
même pour les femmes aux âges avancés. Cependant, on
remarque un pic prononcé à 18 ans qui serait peut-être
dû à la surmortalité généralement
observée chez les enfants issus des femmes très jeunes
ajouté à un transfert des naissances issues des femmes de mois de
18 ans qui déclarent avoir 18 ans. Ça peut être dû
aussi au faite que c'est âge l'égal d'entrée en union. En
effet, les jeunes mères en union au moment de l'enquête
chercheraient à déclarer un âge de 18 ans pour
légaliser leur union, tout au moins socialement, dans un pays où
les unions libres sont réprimandées. Or, les enfants nés
de ces dernières courent plus le risque de mourir que ceux issus des
femmes un peu plus âgées. Cette hypothèse est
confortée par le fait qu'aux âges 15, 16 et 17 ans il n'y a eu
aucun décès déclaré. Ce qui n'est pas vraisemblable
puisqu'au cas où on supposerait que l'échantillon est
représentatif, cela voudrait que durant les quatre années
précédent les douze mois avant l'enquête les enfants
nés vivants issus des femmes âgées de 15 à 17 ans au
moment de l'enquête n'ont couru aucun risque de décès.
Ainsi, nous exclurons ces enfants de nos analyses ultérieures. Cela ne
causera pas de problèmes du fait qu'ils ne représentent que 0,2%
de l'ensemble des enfants nés vivants dans cette période.
Une première correction peut être
effectuée en agrégeant les données par groupe d'âges
quinquennaux.
Graphique 2. 6 : Proportion d'enfants
décédés selon le groupe d'âges des mères au
moment de l'enquête.

L'étude du graphique précédent montre une
croissance régulière de la proportion d'enfants
décédés à partir du deuxième groupe
d'âge (20-24 ans). La proportion élevée observée
pour le premier groupe s'expliquerait comme nous l'avons dit par la
surmortalité observée les mères très jeunes. Cela
peut provenir aussi au faible effectif des enfants issus de ces femmes. Cela
nous permet d'affirme que malgré qu'il y ait eu de mauvaises
déclarations, l'agrégation des données sur les
décès des enfants permet de les corriger.
c.2.3. Evaluation des
données sur l'âge de l'enfant au
décès
Graphique 2.7 : Répartition des
décès de moins d'un an selon l'âge en mois

Dans les pays en développement, l'insuffisance du suivi
médical de la grossesse, de l'accouchement et du nouveau-né,
joint à d'autres facteurs culturels, entraînent le plus souvent un
nombre important de décès au cours du premier mois de la vie. Ce
nombre de décès diminue régulièrement au fur et
à mesure que les enfants avancent en âge. Cette tendance est
confirmée par la proportion des décès néonatals
dans la mortalité infantile qui ne devrait pas s'écarter de un
tiers (Akoto, 1985). Le calcul de la proportion des
décès néonataux dans la mortalité infantile,
à partir des données de l'EDSR-III est de 0,47 (confer graphique
précédent). Cette dernière est largement supérieure
au tiers. De plus, on observe certaines irrégularités comme une
petite diminution à 5 mois suivie d'une augmentation à 6 mois et
une forte augmentation à 9 mois suivie directement d'une forte baisse
à 10 mois. Cela suggère une l'existence petite attraction
à 6 mois et une autre plus importante à 9 mois. Néanmoins,
l'allure générale de la courbe montre que ces attractions ne sont
pas d'ampleur à entraver la qualité des résultats des
analyses d'autant plus que l'étude ne distinguera pas les
décès des enfants par mois d'âge. Ainsi, nous en concluons
que les imperfections observées sont faibles pour compromettre
l'utilisation des ces données.
| 


