Mise en place d'une technologie voip et d'une téléassistance dans une institution d'enseignement supérieur et universitaires; cas de l'ISTIA Kabinda

II..4.2.1.3. Méthode Program Evaluation And Review Technic (PERT)

La méthode PERT est une technique permettant de gérer l'ordonnancement dans un projet, elle consiste à représenter sous forme de graphe, un réseau de tâches dont l'enchaînement permet d'aboutir à l'atteinte des objectifs d'un projet (³⁴).

La méthode PERT (Program Evaluation and Review Technique) utilise une représentation en graphe pour déterminer la durée minimum d'un projet connaissant la durée de chaque tâche et les contraintes d'enchaînement. Elle est complétée par l'établissement du diagramme de Gantt le graphe des tâches. Son but est de :

Trouver le bon enchainement des taches pour que l'ensemble du projet soit réalisé dans les délais convenables ;

Identifier les marges existantes sur les tâches avec dates du début (au plus tôt et au plus tard) ;

³⁴ KAMBAJA,J., Op.Cit

Page 58 sur 119

Identifier les activités critiques pour leur assurer une gestion rigoureuse ;

Etudier les couts en rapportant les activités qui nécessitent les mêmes ressources et faire une meilleure affectation des ressources ;

Prévoir à l' avance les actions correctives à entreprendre en cas de retard ou de dépassement des charges et Suivre quotidiennement l'état d'avancement de projet.

Cette méthode présente les caractères suivants :

Un et un seul node initial, un et un seul node terminal ; contrainte dont peu de packages tiennent compte ;

Un et un seul arc entre chaque paire de nodes connectées :

Caractéristique non obligatoire en notation A on N

Pour le réseau en notation A on A, et des arc sont à créer si cette propriété n'existe pas.

Pas de circuit ;

Pas de boucles ;

Au moins un chemin de node initial jusqu'à tous les nodes suivants, et en particulier le node terminal.

A chaque activité, peut être assignée une durée déterminée ou probable, idem par chemin.

La durée du projet entier est celle du plus long chemin le composant (chemin critique). Les activités sur ce chemin sont des activités critiques.

Il peut y avoir plus d'un chemin critique. Tout délai ou temps consommé pour la réalisation d'une activité appartenant à chaque chemin, augmente la durée de projet global, tandis que des délais apportés sur les activités non critiques ne reconduisent pas à la même conséquence.

II.4.3. Problèmes d'ordonnancement

II.4.3.1. But de l'ordonnancement

Il s'agit d'ordonner dans le temps un ensemble d'opérations contribuant à la réalisation d'un même projet.

Pour définir un problème d'ordonnancement, il faut :

Décomposer le problème en tâches élémentaires ;

Respecter certaines contraintes qui peuvent être :

Soit les contraintes d'antériorité :

Une tâche j ne peut commencer que lors qu'une tâche i est terminée (contrainte de succession) ;

Une tâche j ne peut commencer qu'un certain laps de temps après la tâche i ait commencée.

2) Soit des contraintes de date :

Une tâche ne peut commencer avant une certaine date (indépendamment du fait qu'elle soit succédée à d'autres tâches).

L'objectif consiste à minimiser la durée totale de la réalisation du projet : Compte tenu de la durée nécessaire à la réalisation de chacune des opérations ;

Page 59 sur 119

Compte tenu des contraintes qu'elles doivent respecter.

Résoudre un problème d'ordonnancement c'est choisir parmi toutes les solutions, celle qui est optimale à partir d'un critère fixé à priori.³⁵

II.4.3.2. Avantages du modèle d'ordonnancement choisi Le modèle d'ordonnancement a comme avantages :

Ø De faciliter l'établissement d'un planning optimal de réalisation des tâches dans un projet ;

Ø D'indiquer l'ordre de déroulement des opérations, c'est-à-dire l'exécution des tâches ;

Ø De minimiser la durée totale de réalisation du projet ;

Ø De définir avec exactitude les dates de début des travaux au plus tôt et celle de fin des travaux au plus tard.

³⁵ KAMBAJA,J., Op.Cit

Page 60 sur 119

II.4.3.3. Identification des taches du projet

Le tableau suivant comprend toutes les tâches identifiées, les opérations ainsi que la durée de la réalisation de chacune d'elles.

Tableau n°6

TACHES	LIBELLE	TACHESS ANTERIEURS	DUREE (JOURS)
A	Création du Groupe de travail	-	5
B	Prise de contact	A	3
C	Analyse de besoin	B	7
D	Rapport de l'Analyse	C	2
E	Critique du système d'information	D	4
F	Etude des Scénarios	E	4
G	Etablissement du Cahier des Charges	F	10
H	Inventaire des matériels	G	4
I	Appel d'offre	H	6
J	Dépouillement d'offres	I	1
K	Achat des matériel	J	25
L	Acquisition des matériels	K	1
M	Installation des matériels	L	4
N	Conception de l'architecture du réseau LAN avec la VoIP	H	15
O	Implémentation du réseau avec la VoIP	N,M	40
P	Teste du fonctionnement	O	20
Q	Formation des utilisateurs	P	12
R	Lancement	Q	1
TOTAL JOURS			164

Source : Nous-même

Page 61 sur 119

II.4.3.4. Estimation des couts pour la réalisation du projet

Nous distinguons trois méthodes d'estimation de charges à savoir :

V' La méthode Delphi ;

V' La méthode de répartition proportionnelle, et ;

V' La méthode COCOMO.

Dans le cadre de notre travail, nous avons choisi la méthode de répartition proportionnelle

qui permet d'identifier analytiquement les tâches à entreprendre dans les phases du

projet et ensuite, dégager une synthèse avec une estimation des charges globales qui seront

réparties proportionnellement pour chaque cycle de vie 30.

Ainsi, nous avons

Scope d'application : 3% de la charge totale ;

Spécification des besoins utilisateurs : 3% de la charge globale ;

Architecture de l'application : 20% de la charge de réalisation ou

développement ;

Développement : 2 fois la charge spécification des besoins ;

Test : 5% de la charge de développement ;

Planification : 2% de spécification des besoins utilisateurs.

Arc

Page 62 sur 119

II.4.3.5. Détermination des charges

Tableau n°7

TACHES	LIBELLE	TACHESS ANTERIEURS	COUT/$
A	Formation du groupe de travail	-	500
B	Prise de contact	A	120
C	Analyse de besoin	B	50
D	Rapport de l'analyse de besoin	B	100
E	Bilan	D	120
F	Etude de scenarios	E	250
G	Cahier des charges matériels et logiciels	F	15985
H	Inventaire des matériels	G	100
I	Appel d'offre	H	200
J	Dépouillement des matériels	I	250
K	Commande des matériels	J	70
L	Acquisition des matériels	K	150
M	Installation des matériels	L	150
N	Conception de l'architecture du LAN avec VoIP	H	400
O	Implémentation du réseau avec VoIP	M,N	500
P	Test de fonctionnement	O	90
Q	Formation des utilisateurs	P	700
R	Lancement	Q	50
COUT TOTAL D'EVALUATION (ETE)			19785

Source : nous-même

Nous estimons les imprévus à 400$

CTP (Coût Total du Projet) = CTE + Imprévus = 20.185 $

II.4.3.6. Construction du graphe non ordonne

Pour construire le graff, les sommets se présentent de gauche à droite et entre les deux, on trouve l'Arc qui définit une relation d'antériorité comme nous l'avons dit au debut de ce chapitre.

Figure n°24

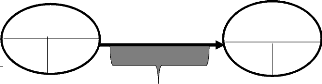
Ti TZ*

X

Ti TZ*

X

Sommet

Source : Nous-même

Page 63 sur 119

X: le noeud de la tâche;

Ti: la date de début ou date au plus tôt de la tâche; II.4.3.7. Principes de présentation

Il y a deux notations pour présenter le graphe PERT : A on A qui signifie activité sur l'arc et A on N qui signifie activité sur le noeud.

Dans le cadre du présent travail, nous utiliserons la notation A on A pour une meilleure représentation en fin de ne pas prêter des confusions.

Un sommet du graphe correspond à un noeud ;

Un arc du graphe définit l'opération ou la tâche ;

La longueur de l'arc donne le temps minimum qui doit s'écouler entre le début de la tâche d'origine et le début de la tâche d'extrémité finale.

Date au plutôt

D'une manière générale, la date au plutôt d'un sommet i d'un graphe PERT commence par le sommet 1, est la marque i du sommet i dans la recherche du chemin de longueur maximal pour relier 1 à i (1).

ü Date au plus tard

Si un retard se produisait sur une opération critique, le projet est d'autant retardé, la date à laquelle se termine cette opération est aussi retardée. Pour calculer cette date, il faut partir du sommet. Obtient obligatoirement l'égalité entre la date les plutôt et les dates au plus tard.

· Calcul des marges libres et marges totale

La marge libre est le délai qu'on dispose pour la mise en route de la tâche (i) sans dépasser la date au plutôt (³⁶).

Pour la tâche i, cette marge si on la dépasse, certaines tâches suivantes sont retardées. Pour calculer la marge libre, la formule est la suivante :

· Marge Totale (MT)

La marge totale d'une tâche (i) le délai de frottement dont on dispose pour la mise en route de la tâche (i) sans dépasser la date au plus tard. Si l'on dépasse la marge totale, la durée du projet va augmenter.

La formule pour trouver la marge totale est la suivante :

· Représentation des dates et des marges

Après avoir estimé les durées de toutes les tâches qui constituent notre graphe, nous pouvons calculer les dates de début et de fin de chacune des tâches. Nous allons procéder comme suit :

(³⁶)KIPUPI KITENGE A., Op.Cit

Page 64 sur 119

· Dates au plus tôt (DTO): ici, nous chercherons à quelles dates au plus tôt peuvent être exécutées les différentes tâches du projet. La technique est la suivante :

- On initialise la date au plus tôt de la première tâche (début) à 0 ;

- S'il n'y a qu'un seul chemin (pour les autres) pour aboutir à une tâche N, alors la date au plus tôt de N = date au plus tôt de i + durée TiN de la tâche i.

- S'il y a plusieurs chemins pour aboutir à N, alors la date au plus tôt N = max[(date au plus tôt i + durée TiN) ; (date au plus tôt K + durée TKN)]

Page 65 sur 119

II.4.3.7. Présentation du graphe non ordonne Figure n°25

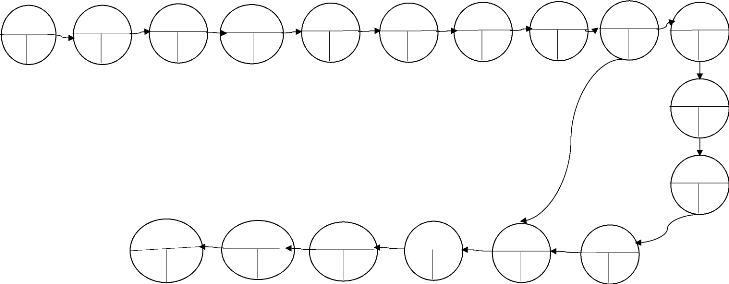
0 0

D A 1 B

5

5 5

3

8 8

2

7

C

15 15

3

2

D

17 17

4

4

E

21 21

5

4

F

25 25

6

G

10

35 35

7

H

4

39 39

8

I

6

9

45 23

1 J

15

N

10

46 24

25 K

11

71 49

1

F

1 16 12

15

20

14

40

13

4

12

L

127 127

R

126 126

Q 114 114

P

94 94

O 54 54

M 72 50

Source : Nous-même

Page 66 sur 119

II.4.3.8. Tableau d'enchainement des taches avec durée

Tableau n°8

TACHE	DUREE (JOUR)	Ta	Date de début Plus tard	Date de début Plus tôt	Marche Libre
A	5	-	5	5	0
B	3	A	8	8	0
C	7	B	15	15	0
D	2	B	17	17	0
E	4	D	21	21	0
F	4	E	25	25	0
G	10	F	35	35	0
H	4	G	39	39	0
I	6	H	45	23	22
J	1	I	46	24	22
K	25	J	71	49	23
L	1	K	72	50	22
M	4	L	54	54	0
N	15	H	39	39	0
O	40	M,N	94	94	0
P	20	O	114	114	0
Q	12	P	126	126	0
R	1	Q	127	127	0

Source : Nous-même

Recherche du chemin critique

La recherche du chemin critique consiste à sortir du graphe le chemin qui, formé par la

succession des différentes tâches, nous donne le temps le plus long (³⁷). Ce chemin est appelé critique car, tout retard pris sur l'une des tâches de ce chemin entraine un retard dans l'achèvement du projet, on part du point terminal et on repère toutes les étapes qui satisferont l'égalité suivante : date au plus tard, date au plutôt, durée de (i) = 0 DTA-DTO-d (i) = Tâches critiques : A,B,C,D,E,F,G,H,N,O,P,Q,R

Chemin critique : A B C D E F G H N O P Q R

Nombre Total de la marge : 89

Pour calculer la durée du projet on fait la sommation de durée de taches critiques.

Nombre Total de la durée : 131 Jours

(³⁷) Seraphin NGOYI., op.cit

Page 67 sur 119

II.4.3.9. Présentation du graphe ordonné

Le graphe Ordonné c'est le chemin critique qui est défini par l'ensemble des tâches dont les dates au plus tôt sont égales aux dates au plus tard, c'est-à-dire l'ensemble des tâches dont les marges totales sont nulles. Voici notre chemin critique:

Figure n°

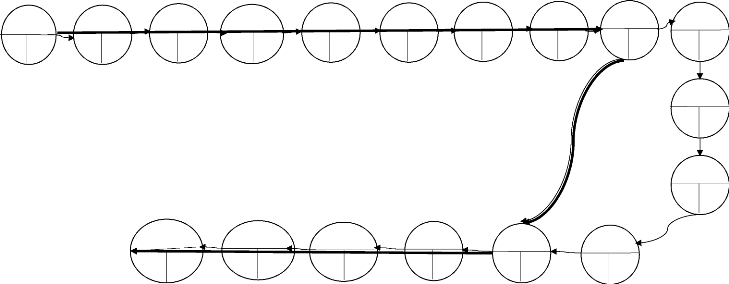
22

D A 1 B

2

C

3

D

4

E

5

F

6

G

7

H

8

I

9

0 0

5 5

3

8 8

7

15 15

2

17 17

4

21 21

4

25 25

10

35 35

4

39 39

6

45 23

5

1 J

15

N

10

46 24

25 K

11

71 49

1

F

1

L

15

20

14

40

13 4

12

127 127

R

126 126

Q 114 114

P

94 94

O 54 54

M 72 50

16 12

Source : Nous-même

Page 68 sur 119