1.4.
Méthode d'analyse des données
Pour ces données, l'analyse minutieuse des
caractéristiquessociodémographique et économique des
ménages agricoles a été faite. Cette analyse a
été appuyée par des statistiques descriptives (moyenne,
fréquence relative et écart-type). L'objectif de cette analyse
est de présenter le profil des ménages agricoles et certaines
caractéristiques de l'environnement socioéconomique
immédiat de ces derniers. Une telle description est essentielle dans la
mesure où ces caractéristiques socioéconomiques peuvent
influencer la demande du maïs et de ses dérivés au
Bénin.
De même, la connaissance des élasticités
de la demande en matière de politique alimentaire estfondamentale. Les
élasticités étant les nombres sans dimension et permettent
de prédire, les effetsde changements de certaines variables telles que
les prix et les salaires sur la quantité des biens consommés.Par
exemple, quel sera l'effet d'une augmentation (en pourcentage) du salaire ou
des prix (du maïs ou des autres biens) sur la demande du maïs.
Ilfaut cependant noter que ce schéma est théorique et que la
demande alimentaire subit, trèssouvent, l'influence de certaines
variables extra-économiques, notamment socioculturelles (Ethnie,
Religion, Age, Sexe, Classe sociale etc...). Concernant l'analyse des
données proprement dite, nous avons utilisé le logiciel
SATAT12
1.4.1.
Présentation du modèle à utiliser
Pour estimer les élasticités, nous avons
adopté le modèle AIDS (AlmostIdealDemand System) qui a
été proposé par Deaton&Mullebauer (1980). Comme son
nom l'indique, c'est jusqu'à maintenant le meilleur modèle pour
estimer une fonction de consommation. Sa popularité provient du fait que
le modèle AIDS est très général (il n'exige pas une
spécification explicite de la fonction d'utilité), facile
à estimer (étant linéaire), et il est conforme avec les
restrictions de la théorie économique qui sont nécessaires
afin d'assurer une maximisation de l'utilité du consommateur. Le
modèle AIDS s'écrit comme suit:
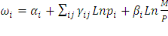 (1) (1) 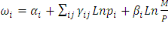
Où 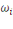 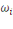 sont les coefficients budgétaires ; sont les coefficients budgétaires ;
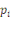 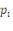 : les prix des biens : les prix des biens  , ,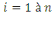 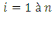 ; ;
M : la dépense totale par tête ;
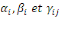 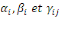 sont les paramètres à estimer ; sont les paramètres à estimer ;
P : une approximation linéaire de l'indice de Stone qui
s'écrit :
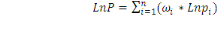 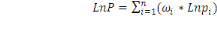 .. ..
L'équation relie donc, les coefficients
budgétaires des biens avec le logarithme des prix à la
consommation et de la consommation réelle. Pour qu'il soit issu de la
maximisation d'une fonction d'utilité, le système
d'équations va être estimé sous les contraintes
d'additivité (1.1), d'homogénéité (1.2) et de
symétrie (1.3).
(1.1) Additivité
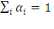 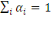 ; ;
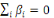 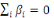 ; ;
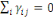 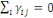 ; ;
(1.2) Homogénéité
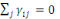 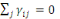 ; ;
(1.3) Symétrie
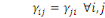 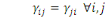 . .
· Méthode d'estimation
Cette méthode d'estimation a été
utilisée par Oloukoi et Adégbola (2005b) lorsqu'ils cherchaient
à estimer les élasticités de demande des amandes de noix
d'anacarde au Bénin.
- Coefficients budgétaires 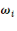 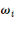 : La technique a consisté à calculer dans un premier temps
les coefficients budgétaires c'est-à-dire la part que
représentent les dépenses sur un bien i dans les
dépenses totales du ménage. : La technique a consisté à calculer dans un premier temps
les coefficients budgétaires c'est-à-dire la part que
représentent les dépenses sur un bien i dans les
dépenses totales du ménage.
- Indice de Stone P : Pour l'indice de
Stone, d'abord le logarithme népérien des prix d'achat moyens de
chaque bien a été calculé. Ensuite, le logarithme
népérien de l'indice de Stone a été obtenu par la
somme du produit des coefficients budgétaires et du logarithme
népérien des prix d'achat moyens de chaque bien.
- Dépenses par ménage M :
Le logarithme népérien des dépenses a été
obtenu par le logarithme népérien du montant total alloué
par chaque ménage à l'acquisition des neuf biens
considérés. Les informations sur les revenus ne sont pas souvent
fiables. Il a été préféré dans cette
étude d'utiliser les dépenses totales de consommation issues des
enquêtes auprès des ménages. Le niveau de consommation
varie très peu d'une saison à une autre contrairement au revenu.
Selon Ravelosoa et al (1999), «la consommation, qui varie moins, est
considérée comme une mesure plus exacte du revenu permanent des
ménages, et pour cette raison elle est souvent considérée
préférable comme mesure agrégée du bien-être
du ménage ».
- Dépenses réelles par ménage
M/P : Le logarithme népérien des dépenses
réelles est le logarithme népérien du rapport de M et de
P.
- Elasticités : Les
élasticités revenus et prix sont déduites de ces
estimations par les relations suivantes:
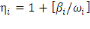 (1.3) (1.3) 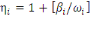
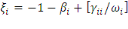 (1.4) (1.4) 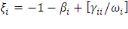
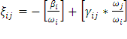 (1.5) (1.5) 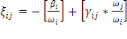
Où 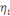 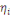 représente l'élasticité de la demande, représente l'élasticité de la demande, 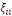 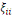 l'élasticité prix propre et l'élasticité prix propre et 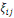 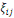 l'élasticité noncompensée de Marshal. l'élasticité noncompensée de Marshal.
| 


