1.6.4 Démarche de la méthode
La méthode AHP a recours à différentes
formes de connaissances, au fur et à mesure de
son déroulement. Elle fait en particulier appel
à l'imagination et à l'expérience pour définir la
hiérarchie du problème. Lors du diagnostic ou de l'expertise,
elle fait appel à la logique et à l'intuition des
décideurs pour proposer des appréciations. Elle permet ainsi
d'identifier, de comprendre et d'évaluer les interactions d'un
système considéré dans sa globalité (T.Saaty,
1980)
La méthode AHP est construite à partir de
différents niveaux de critères. Elle permet ainsi
? décomposer un problème complexe et non
structuré en ses éléments constituants.
? modéliser ces éléments sous la forme
d'une structure hiérarchique.
? quantifier l'importance relative de chaque
élément à partir de jugements subjectifs.
? et enfin, de synthétiser l'importance relative de
chaque élément de la hiérarchie en une
préférence globale afin de déterminer des priorités
parmi les actions potentielles.
La méthode AHP permet de compenser la
dégradation de performance d'une action sur certains critères par
sa performance sur d'autres. Une telle méthode est dite compensatoire.
Afin de mesurer les qualités intangibles d'éléments de
nature différente, elle repose sur l'utilisation d'une échelle de
mesure unique. Elle permet ainsi de résoudre un grand nombre de
problèmes décisionnels de façon quantitative en
élaborant un modèle d'aide à la décision,
représenté sous la forme d'une hiérarchie, elle repose
principalement sur une démarche descriptive afin de tenir en compte la
nature « humaine » plutôt que de lui imposer un mode de
pensée particulier.
1.6.4.1 Les étapes de l'application
Nous allons détailler dans ce qui va suivre les
différentes étapes de la méthode AHP (voir la figure
1.4).
13
Chapitre 1 Aide à la décision
Multicritère
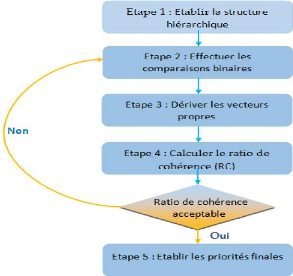
Figure 1.4 les étapes d'application de
l'AHP
Étape 1 : Etablir la structure
hiérarchique
La première étape consiste à
décomposer le problème complexe en une structure
hiérarchique à travers des niveaux qui sont :
Niveau 0 : Définir l'objectif cible.
Niveau 1 : Définir les critères de
décision ou d'analyse.
Niveau intermédiaire : Il peut y avoir
plusieurs pour déterminer les sous critères
Dernier Niveau : Définir les alternatives
ou les actions possibles.
La figure 1.5 donne un aperçu sur la hiérarchie
d'un problème.
14
Chapitre 1 Aide à la décision
Multicritère
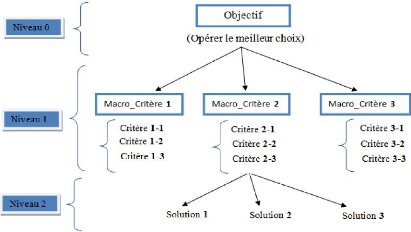
Figure 1.5 la hiérarchie du
problème
Étape 2 : Effectuer les pondérations
binaires
Cette étape consiste à étudier les points
suivants :
- Comparer l'importance relative de tous les
éléments appartenant à un même niveau de la
hiérarchie pris deux par deux, par rapport à
l'élément du niveau immédiatement supérieur. -
configurer une matrice carrée réciproque formée par les
évaluations (K*K), K étant le nombre d'éléments
comparés, nous obtenons une matrice (voir exemple).
aij = 1 et
a = aij avec aji = liaij (valeur réciproque)
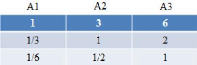
Tableau 1.1 Exemple d'une matrice de
comparaison par paire.
Chapitre 1 Aide à la décision
Multicritère
Degré de préférence
|
1
|
|
Importance égale
|
|
|
|
|
2
|
|
Importance faible
|
|
3
|
|
Importance assez modérée
|
|
|
|
|
4
|
|
Importance modérée
|
|
5
|
|
Importance assez forte
|
|
6
|
|
Importance forte
|
|
7
|
|
Importance très forte
|
|
8
|
|
Importance extrême
|
|
|
|
|
9
|
|
Importance capitale
|
Tableau 1.2 Echelle de Saaty (Fiat, 2007).
Étape 3 : Déterminer les vecteurs
propres
La détermination des priorités des
éléments de chaque matrice se fait par la résolution du
problème de vecteurs propres. Calculer l'importance relative de chacun
des éléments de la hiérarchie à partir des
évaluations obtenues à l'étape précédente,
et l'importance relative des différents critères est
exprimée par les valeurs du vecteur propre normalisé à 1.
Plus grande est cette valeur et plus important est le critère
correspondant.
Étape 4 : Calculer le ratio de
cohérence (RC)
Les réponses obtenues présentent souvent un
certain degré d'incohérence. La méthode AHP n'exige pas
que les jugements soient cohérents ni transitifs, par contre Saaty a
défini un indice de cohérence (IC). Plus l'indice de
cohérence devient grand et plus les jugements de l'utilisateur sont
incohérents et vice versa. IC est ensuite comparé à des
valeurs critiques obtenues par simulation. Saaty a
défini, par expérimentation, un ratio de cohérence comme
le rapport de l'indice de cohérence calculé sur la matrice
correspondante aux jugements du décideur et de l'indice aléatoire
(IA) d'une matrice de même dimension. Une idée est donnée
dans le tableau 1.3.

Tableau 1.3 Les indices de cohérence
aléatoire Satty (1984).
15
16
Chapitre 1 Aide à la décision
Multicritère
Le ratio de cohérence est donné par la formule
suivante :
RC = IC/I??
RC : est le ratio de cohérence.
IA : est un indice aléatoire.
IC : est l'indice de cohérence.
L'indice de cohérence aléatoire est calculé
par cette formule :
IC = ( ??max - K) / (K - ??)
Avec : K est le nombre d'élément
comparé ëmax est la valeur propre maximale.
Le ratio de cohérence peut être
interprété comme la probabilité que la matrice soit
complétée aléatoirement. La cohérence globale
d'appréciation est évaluée au moyen de ce ratio de
cohérence RC. Toujours selon Saaty, la valeur de ce dernier doit
être au plus égale à 10%. Dans le cas où cette
valeur dépasse 10%, les appréciations peuvent exiger certaines
révisions.
Une fois calculé, le ratio de cohérence (RC)
final doit être vérifié selon le niveau acceptable
proposé par (T.Saaty, 1980) en fonction de la taille de la matrice.
Lorsque le ratio de cohérence dépasse la valeur respective du
tableau ci-dessous, on considère que les jugements sont trop
aléatoires. Il faut alors réviser l'analyse afin de parfaire les
jugements et ainsi, obtenir un ratio de cohérence final qui soit
acceptable. Les valeurs données dans le tableau 1.4 montrent les ratios
de cohérence acceptables par Saaty.
|
Taille de la matrice (n)
|
|
Ratio de cohérence acceptable
|
|
3
|
|
0,05
|
|
|
|
|
4
|
|
0,08
|
|
5 et +
|
|
0,10
|
Tableau 1.4 Les ratios de cohérence
acceptable (Satty, 1984). Étape 5 : Etablir les
priorités finales
17
Chapitre 1 Aide à la décision
Multicritère
Le principe de la synthèse des priorités est de
multiplier les priorités locales de chaque niveau par les
priorités globales du niveau père pour obtenir les
priorités globales de toute la hiérarchie par la suite on ajoute
les priorités globales du niveau le plus bas (généralement
ce sont les alternatives).
| 


