Chapitre 3- Procédure de synthèse d'une
cellule capacitive
3.2.3.1 Transformation passe-bas/coupe-bande
Nous allons transformer le filtre passe-bas avec inverseurs
d'admittances idéaux de la Figure 2. 16 en un filtre
coupe-bande avec inverseurs d'admittances correspondant en s'appuyant sur les
transformations de la Figure 3. 6 [28, pp. 727-729].
On obtient le filtre coupe-bande d'ordre 3 constituée de
trois résonateurs séries séparés par deux
inverseurs d'admittance représenter sur la Figure 3. 7.
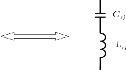
Figure 3. 6: Opération de transformation
d'un filtre passe-bas en un filtre coupe-bande.
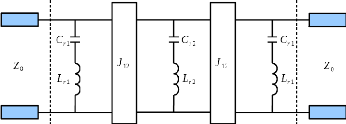
Figure 3. 7: Filtre coupe-bande avec inverseurs
d'admittances
Les éléments des résonateurs séries
(?????? - ??????) sont calculés en utilisant l'équation (3.
1).
?? ?? ?????????? = = ' ?????? (3. 1)
?????????? ??????
- ??1' : représente la
fréquence de coupure du prototype passe-bas normalisé ; cette
dernière est égale à 1.
- ???? : pulsation associée à la fréquence
du zéro.
Finalement, Les valeurs des résonateurs série
(????1 - ????1) et (????2 - ????2) sont données par les
équations (3. 2) et (3. 3).
|
??.??????
=
|
(3. 2)
??????.????.??
|
????
|
??.??????
=
|
(3. 3)
|
|
??????
??
??
{
=
|
??????
??
??
{
=
|
|
??????
|
??????
??????.????.??
|
3.2.3.2 Implémentation des inverseurs d'admittance
a. Solution 1 : Structure en pi avec des inductances
On utilise le circuit équivalent de l'inverseur
d'admittance de la Figure 2. 19 et on aboutit au circuit de la
Figure 3. 8.
55
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
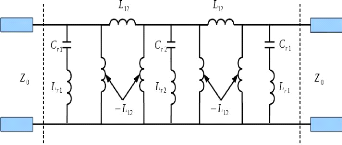
Figure 3. 8: Filtre coupe-bande d'ordre 3
constitué de résonateurs séries et de deux structures en
pi avec des selfs
b. Solution 2 : Structure en pi avec des capacités
On remplace les inverseurs d'admittance par la structure en pi
avec capacités de la Figure 2. 22. Et on obtient le circuit de
la
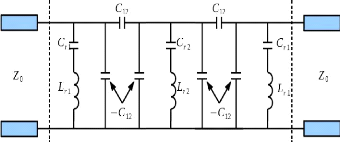
Figure 3. 9: Filtre coupe-bande d'ordre 3
constitué de résonateurs séries et de deux structures en
pi avec capas
A ce niveau, il nous est impossible d'intégrer les
inductances ou capacités négatives parallèles aux
résonateurs séries.
3.2.3.3 Equivalence de la structure en T centrale avec la ligne
(2h ; Zc)
On montre que la structure en T centrale des figures obtenue
après implémentation des inverseurs d'admittances est
équivalente à la ligne de longueurs 2h et d'impédance
caractéristique Zc à la condition que la relation (2.
13) soit vérifiée.
a. Solution 1 : Structure en pi avec des inductances
On aboutit au circuit illustré sur la Figure 3.
10. Ce dernier est composé de deux résonateurs
d'entrée/sortie identiques séparés par une ligne de
longueur 2h et d'impédance caractéristique Zc. Les
résonateurs d'entrée/sortie sont constitués de la mise en
parallèle d'un résonateur série (Lr1 - Cr1) avec une
inductance négative -L12.
b. Solution 2 : Structure en pi avec des capacités
Dans ce cas, le quadripôle équivalent
synthétisé est le même à la différence que
les résonateurs d'entrée/sortie sont ici composés par la
mise en parallèle d'un résonateur série (Lr1 - Cr1) avec
une capacité négative -C12 (cf. Figure 3. 11).
| 


