Chapitre 3- Procédure de synthèse d'une
cellule capacitive
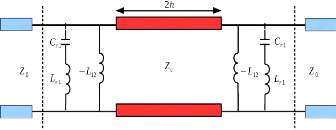
Figure 3. 10: Quadripôle équivalent
obtenue avec la solution 1
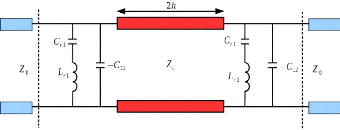
Figure 3. 11: Quadripôle équivalent
obtenu avec la solution 2
A l'issue de cette synthèse, les quadripôles
équivalents obtenus avec les deux solutions sont différents du
quadripôle souhaité de la Figure 3. 2.
Dans la prochaine étape, nous essayerons de simplifier ces
circuits et ainsi déterminer les composants (??1"
- ??1") du quadripôle équivalent final.
3.2.3.4 Détermination des éléments des
circuits
a. Solution 1 : Structure en pi avec des inductances
??12 = ????0??12
D'après la Figure 3. 8,
{2????2????2)
??2 " = ?? ??12??0(??0
2+??0 2????2(??12-2????2)
Avec la première équation du système
ci-dessus et celle du système (2. 13) on trouve que :
?????? = ??????????
????
= ?????? (?? ??) (3. 4)
????
??
56
1
A partir de la seconde et sachant que ????2????2 = 2 , on trouve
les valeurs de ????2 ???? ????2
????
|
?????? = (?? - ???? ??) [??????(??????)
?? ???????? - ??
???? ????????]
????
{
?????? = ??
???? ????????
|
(3. 5)
|
En remontant les équations, on trouve ????2 à
partir de la relation (3. 3), puis ????1 avec l'équation (2. 3) et enfin
????1 ???? ????1 peuvent être obtenus en appliquant la relation (3.
2).
Mais un problème important se pose dans la
réalisation de ces cellules, car nous ne savons pas encore faire des
inductances négatives.
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
Pour des phases à ??0, ??11(??0) ?
[90°;180°], ??12 est de l'ordre de 10-8. Cette
valeur est obtenue avec l'équation (3. 6). De ce fait, nous ne pouvons
pas négliger son impact dans le circuit ni l'associer aux autres
éléments puisqu'elle est montée en parallèle. Donc
nous utiliserons la solution 2 pour synthétiser des phases à ??0,
??11(??0) ? [90°;180°] même si, a priori les résultats
obtenus avec la solution 1 seraient meilleurs comme dans le cas passe-bande.
b. Solution 2 : Structure en pi avec des capacités
??12 = 1/????0??12
D'après la Figure 3. 9, {1-??0
2????2????2
??2 " = ????0[????2-2??12+2????2????2??12??0 2]
|
De la même manière on trouve :
?????? = ?????? ????
Ensuite :
|
-??
=
??????????????(????) (3. 6)
|
(3. 7)
????1 ???? ????1 peuvent ainsi être déterminer avec
la relation (3. 2).
?????? = (?? - ???? ??) [??????(??????)
??
???????? - ????????]
????
{ ??
??????= ???? ????????
57
Pour des phases ??11(f0) ? [-180°; -90°]
??12 est de l'ordre de 10-15 (3.8), son impédance
??12 sera de l'ordre de 104 qui est très grand. Donc ??12
sera vue comme un circuit ouvert dans le circuit. Le quadripôle de la
Figure 3. 11 peut dès lors être simplifier pour obtenir
le quadripôle équivalent de la Figure 3. 2.
Avec : {???? " = ?????? (3. 8)
???? " = ??????
3.3 Résultats de la synthèse
Dans cette partie nous allons déterminer la
précision de la méthode de synthèse
développée précédemment. Nous allons
considérer deux familles de spécifications sur la loi de phase.
Dans la première famille, la phase à ??0, ??11(??0) est positive
et varie de 0° à 180° avec une dispersion
???11(??0) = 30°/?????? alors que dans la
deuxième famille, elle est négative et varie de 0° à
- 180° avec la même dispersion. Nous ne présenterons ici que
les résultats obtenus avec la solution 2.
3.3.1 Première famille de spécification : ??11(??0)
> 0°
Les résultats de la synthèse pour ??11(??0) =
100° et ??11(??0) = 120° avec une dispersion constante égale
à ???11 = 30°/?????? sont présentés à travers
la Figure 3. 12. Le Tableau 3. 3 donne les erreurs moyennes
et maximales des différentes cellules synthétisées pour
des phases à ??0, ??11(??0) > 0°.
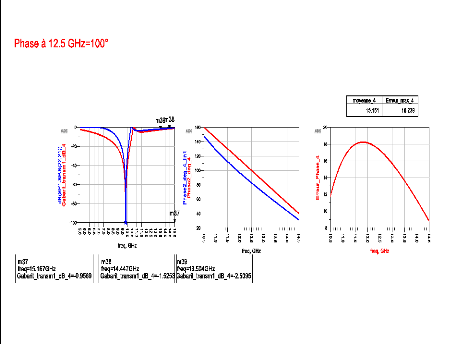
(a)
58
| 


