Chapitre 3- Procédure de synthèse d'une
cellule capacitive
52
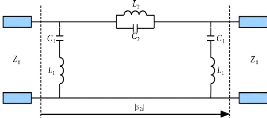
Figure 3. 3: Prototype de filtre
coupe-bande
3.2.2 Spécifications
Comme souligné à la section 2.2.2, lorsque les
zéros de transmissions basses et hautes de la réponse en
amplitude du gabarit entrent dans la zone d'intérêt [10,5-14,5]
GHz, la réponse du filtre s'apparente à celle d'un filtre
coupe-bande d'ordre n=3. La Figure 3. 4 présente les lois de
phase à synthétiser dans le cas d'une phase à
??0 positive ??11(??0) = 160° (Figure 3. 4 (a)) et
dans le cas où elle est négative ??11(??0) = -160°
(Figure 3. 4(b)). Ces dernières sont obtenues avec la
même dispersion fréquentielle ???11 = -30°/?????? et sont
étudiées dans la bande d'intérêt [10,5-14,5] GHz
avec ??0 = 12,5??????.
Ces lois sur la phase en réflexion peuvent dès
lors être traduites en une loi sur l'amplitude en transmission sur les
deux axes du quadripôle équivalent (Figure 3. 5). Les
gabarits en transmission des Figure 3. 5(a) et Figure 3. 5(b)
sont respectivement associés aux lois de phase des Figure 3.
4(a) et Figure 3. 4(b).
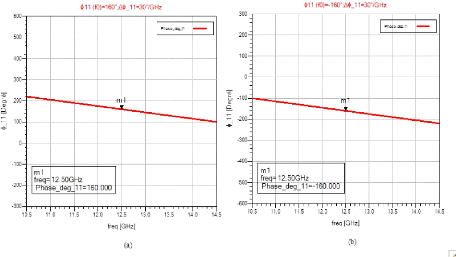
Figure 3. 4: Lois de phase à
synthétiser dans la bande d'intérêt [10,5- 14, 5] GHz. (a)
?11(f0) = 160°. (b) ?11(f0) = -160°
La zone remarquable que nous allons maintenant approximer est
celle contenant le zéro de transmission et non celle contenant le
pôle comme dans d'une cellule inductive.
A partir du gabarit en transmission, nous allons relever
différents paramètres décrivant le zéro de
transmission à savoir : la fréquence du zéro de
transmission ???? ????????, l'ondulation ??????
???????? prise
??11(??0) est négative ou après la bande
rejetée quand
avant la bande rejetée quand la phase à
??0,
53
Chapitre 3- Procédure de synthèse d'une
cellule capacitive
??11(??0) est positive et ??1????????, ??2???????? les
fréquences de coupures basse et haute définies à
l'ondulation ??????
????????.
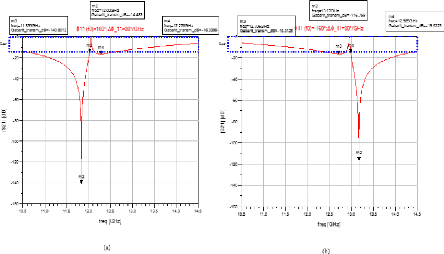
Figure 3. 5: Gabarits en transmission associés
aux lois sur la phase en réflexion (a) ?11(f0) = 160°. (b) ?11(f0)
= -160°.
Le Tableau 3. 1 donne les valeurs de ces
paramètres pour les spécifications précédentes. Ces
valeurs serviront ensuite à paramétrer la réponse du
prototype coupe-bande. En appliquant les formules de la section 2.3.3, on
obtient les valeurs des paramètres coupe-bande du Tableau 3.
2.
|
???11(°/??????)
|
??11(??0)(°)
|
???????? (????) ??????
|
?????? ?????? (??????)
|
??1?? ?????? (??????)
|
??2?? ?????? (??????)
|
|
-30
|
160
|
16,347
|
11,833
|
-
|
12,012
|
|
-30
|
-160
|
16,347
|
13,164
|
12,988
|
-
|
Tableau 3. 1: Valeurs des paramètres du
gabarit à synthétiser
|
???11(°/??????)
|
??11(??0) (°)
|
????9 (????) ??????
|
???? ???? (??????)
|
??1???? (??????)
|
??2 ???? (??????)
|
|
-30
|
160
|
16,347
|
11,833
|
11,657
|
12,012
|
|
-30
|
-160
|
16,347
|
13,164
|
12,988
|
13,342
|
Tableau 3. 2: Valeurs des paramètres de la
réponse du filtre coupe-bande
3.2.3 Synthèse du quadripôle équivalent
La procédure de la synthèse se fait par
étape comme nous l'avions défini dans le cas d'une cellule
inductive. Nous distinguerons aussi deux solutions que nous essayerons
d'exploiter. Les trois premières étapes de cette synthèse
sont équivalentes aux trois premières de celle
développée pour la cellule Phoenix d'ordre de type inductif.
9 L'exposant CB fait référence aux
paramètres du prototype coupe-bande
54
| 


