Chapitre 2- Procédure de synthèse d'une
cellule inductive
La Figure 2. 32 présente l'erreur moyenne en
fonction de la phase à f0, ??11(f0).
Pour une spécification fixée à ??11(f0) = 0°
, l'erreur moyenne entre la loi de phase souhaitée et la phase
réalisée par le dipôle est de 7.545°. Cette erreur
augmente jusqu'à ??11(f0) = -40°, puis diminue
pour des phases à f0 comprises entre
-60° et -90°. Au-delà,
l'erreur augmente fortement.
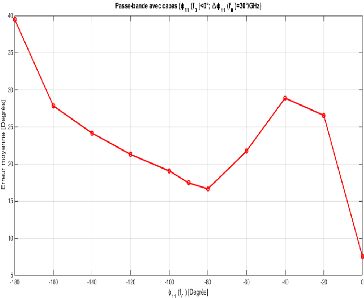
Figure 2. 32: Erreur moyenne solution 2 lorsque
??ll(????) v??r??e de ??° à - l????° ??vec
???ll (?? ??)=-30°/GHz
2.4.2.3 Troisième famille de spécification :
variation de ???11
Pour cette dernière famille, le phase à
f0, ??11(f0), est fixée à
-20° et la dispersion ???11(f0) varie en prenant trois
valeurs : -30°/GHz, -45°/GHz et -60°/GHz. La Figure 2. 33
illustre les résultats de la synthèse. Pour cette
spécification, le pôle du gabarit en transmission se trouve dans
la bande d'intérêt et est presque centré à la
fréquence f0. Le Tableau 2. 8 présente
l'erreur moyenne et l'erreur maximal de la cellule pour chaque dispersion. Nous
remarquons que l'erreur moyenne ainsi que l'erreur maximale augmentent lorsque
la dispersion augmente.
|
???11(°/GHz)
|
??11(f0) (°)
|
Em??y (°)
|
Em??x (°)
|
|
-30
|
-20
|
26,566
|
35,706
|
|
-45
|
-20
|
35,169
|
51,679
|
|
-60
|
-20
|
46,415
|
66,886
|
Tableau 2. 8: Erreurs moyenne et maximale solution
1 avec ??ll (?? ??) = -????° pour chaque
dispersion
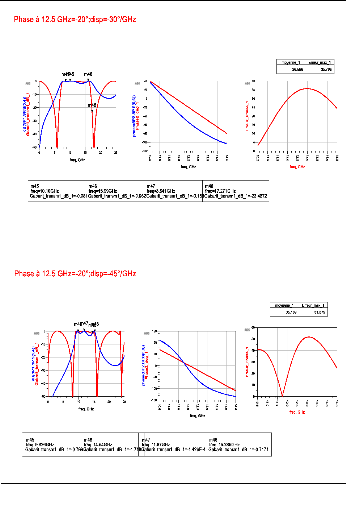
(a)
48
(b)
Chapitre 2-Procédure de synthèse d'une
cellule inductive
49
Chapitre 2- Procédure de synthèse d'une
cellule inductive
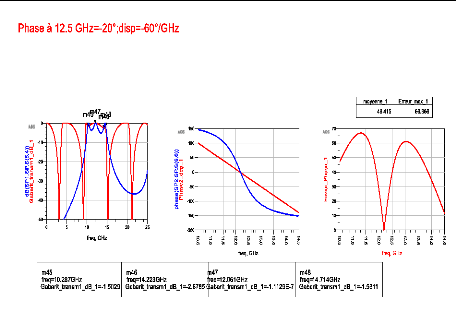
(c)
Figure 2. 33: Résultats de la
synthèse passe-bande solution 2. (a) ???????(??
??)= -30°/GHz. (b) ??????? (??
??)=-45°/GHz. (c)
???????(????)=-60°/GHz
2.4.3 Bilan sur la précision de la procédure de
synthèse passe-bande
La Figure 2. 34 présente l'évolution de
l'erreur moyenne en fonction de ??11(??0) pour trois dispersions ???11(??0) =
{-30°/??????; -45°/??????; -60°/??????}. Pour des valeurs de
?11(f0) comprises entre ]0° ; -40° ]et]0° ; 40°], l'erreur
augmente fortement en fonction de la dispersion. Bien que cette zone soit
idéale, dans le sens où le pôle du gabarit se trouve dans
la bande
40°; -60°/??????).
d'intérêt, l'erreur moyenne atteint une valeur
maximale de 32,914° pour (??11(??0); ???11) = (-
50
Chapitre 2-Procédure de synthèse d'une
cellule inductive
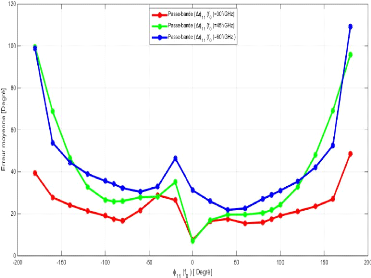
Figure 2. 34: Bilan sur les performances de la
procédure de synthèse de type passe-bande
Pour conclure, les résultats obtenus par l'utilisation
de la synthèse de type passe-bande ne sont pas globalement satisfaisants
et méritent d'être améliorés.
2.5 Conclusion
Dans ce chapitre, nous avons développé une
nouvelle méthode de synthèse d'une cellule Phoenix d'ordre 2 de
type inductif basée sur les techniques classiques de filtrage. Cette
méthode permet la conversion d'une loi à l'entrée d'un
dipôle équivalent en une loi sur le gabarit en transmission entre
les deux accès du quadripôle équivalent. Au cours de la
synthèse, deux solutions ont été retenues : la solution 1,
obtenue en remplaçant les inverseurs d'admittances par une structure en
pi avec des inductances et la solution 2, obtenue par utilisation d'une
structure en pi avec des capacités.
Pour tester les performances de la synthèse et
définir le domaine de validité de chaque solution, nous avons
considéré trois familles de spécifications sur la loi de
phase à synthétiser. Les résultats obtenus
révèlent que selon que ??11(J0) E [0°; 90°] ??u
[0°; -90°] , la solution 1 ou la solution 2 était la plus
appropriée. Ces résultats montrent aussi que dans ces deux
intervalles, la synthèse passe-bande offre de bonne précision qui
mérite néanmoins d'être améliorer et que les
performances se dégradent à mesure qu'on s'éloigne de ces
valeurs.
Nous allons maintenant montrer que pour les autres valeurs de
??11(J0), il est plus judicieux de s'appuyer sur une synthèse
coupe-bande.
Chapitre 3 : Procédure de synthèse d'une
cellule capacitive 3.1 Introduction
Dans ce dernier chapitre, nous proposons une nouvelle
procédure de synthèse appliquée à la cellule
Phoenix d'ordre 2 capacitive en utilisant les techniques classiques de
filtrage. Le motif capacitif de la cellule Phoenix d'ordre 2 se
caractérise par un comportement en amplitude de type coupe-bande d'ordre
3 dans la bande d'intérêt [10,5-14,5] GHz.
L'objectif de cette procédure est de synthétiser
le quadripôle équivalent composé de deux résonateurs
séries d'entrée et de sortie (L1 " - C1 ")
séparée par une ligne de transmission de longueur 2h et
d'impédance caractéristique Z?? (cf. Figure 3.
2) en utilisant le prototype de filtre coupe-bande se rapprochant au mieux
de l'amplitude du gabarit en transmission. Cette structure est
constituée de deux résonateurs séries (L1 - C1)
en parallèles dans le circuit séparés par un
résonateur parallèle (L2 - C2) en
série dans le circuit (cf. Figure 3. 3). L'idée est
comme précédemment de ne plus considérer la ligne centrale
directement comme le résonateur parallèle [2, pp. 149-151] mais
de la découper en plusieurs éléments en passant par
différentes étapes. Ainsi, à chaque configuration
différente correspondra une répartition différente des
valeurs des composants utilisés.
Le principe de la synthèse est le même que celui
du prototype passe-bande vue précédemment. Nous allons
découper le circuit en plusieurs éléments
(résonateurs séries en parallèles dans le circuit et
inverseurs d'admittances) puis intégrer certains éléments
des inverseurs d'admittances dans les résonateurs d'entrée et de
sortie. Les résultats obtenus sur la base de deux familles de
spécifications faites sur la loi de phase en réflexion seront
présentés avant de donner le bilan sur la précision de la
synthèse coupe-bande appliquée au motif capacitif.
3.2 Procédure de synthèse proposée pour une
cellule capacitive
3.2.1 Circuits équivalents
Le circuit équivalent du motif capacitif d'une cellule
Phoenix d'ordre 2 est un dipôle composé par un résonateur
série (L1 " - C1 ") à l'entrée du dipôle et
d'une ligne court-circuitée de longueur h et d'impédance
caractéristique Z?? (cf. Figure 3. 1). Le
quadripôle équivalent est présenté sur la Figure
3. 2. Il est composé de deux résonateurs séries
séparés par une ligne de transmission de longueur 2h et
d'impédance caractéristique Z??.
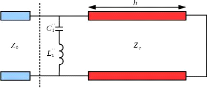
Figure 3. 1: Motif capacitif d'une cellule Phoenix
d'ordre 2
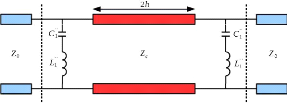
Figure 3. 2: Quadripôle
équivalent
| 


