Synthèse de cellules unitaires de réseaux réflecteurs basée sur des techniques de synthèse de filtres

Chapitre 2- Procédure de synthèse d'une cellule inductive

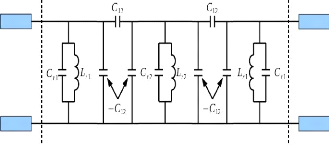
Figure 2. 23: Filtre passe-bande d'ordre 3 constitué de résonateurs parallèles et de deux structures en pi avec des

capacités

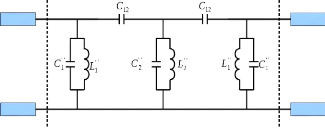
Figure 2. 24: Filtre passe-bande constitué de 3 résonateurs parallèles séparés par deux capacités

{

???? " = ?????? - ?????? (2. 11) et {???? " = ?????? - ???????? (2. 12)
???? " = ?????? ???? " = ??????

2.3.4.6 Equivalence de la structure en T centrale avec la ligne (2h ; ????)

Dans cette étape, on cherche à remplacer la structure centrale en T par une ligne de longueur 2h et d'impédance caractéristique ???? (cf. Figure 2. 25) en utilisant les matrices chaines des deux structures [28, p. 28].

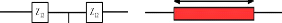
Figure 2. 25: Equivalence entre la structure en T centrale et la ligne (2k, Zc)

On montre finalement que les deux structures de la Figure 2. 25 sont équivalente à la condition que :

?????? ???? " {	= =	????????????(????) ????	(2. 13)
		-?? ??????(??????)

36

Chapitre 2-Procédure de synthèse d'une cellule inductive

On obtient ainsi le circuit équivalent final constituée de deux résonateurs d'entrée et de sortie (??₁^" - ??₁^") parallèles séparés par une ligne de longueur 2h et d'impédance caractéristique ???? (cf. Figure 2. 10).

2.3.4.7 Détermination des éléments des circuits

Les expressions des impédances ??12 et ??₂^" seront définies dans les deux cas (solution 1 et solution 2) et avec le système d'équation (2.13) établit précédemment, nous déterminerons les valeurs des différents composants des circuits obtenues à chaque étape de la synthèse pour obtenir enfin les valeurs des composants (??₁^" - ??₁^") des résonateurs d'entrée et de sortie du quadripôle équivalent.

a. Solution 1 : Structure en pi avec des inductances

Sur la Figure 2. 21, on a : { ??12 = ????0??12 ")

??2 " = ????2 " ??0/(1 - ??02??2 " ??2

La première équation du système ci-dessus et celle du système (2.13) impliquent que :

?? ?????? = ??????????

?? ??????????(????) (2. 14)

1

A partir de la seconde et sachant que ????2????2 = 2 , on trouve les valeurs de ????2 ???? ????2

????

??

(2. 15)

?????? = ????(???? ??-??????)

?? ??????(????)(?? + ??????(????))

??????

??????????

{ ?????? = ??

???? ???????? = ????(??????-??????)??????(????)(??+??????(????))??

b. Solution 2 : Structure en pi avec des capacités

Avec la Figure 2. 24, on obtient : {??12 = 1/????₀??₁₂

??2 " = ????₂ "?? 0/(1 - ??0²??₂^" ??₂^")

De la même manière on trouve

??

?????? = ?????????? = - ??????????(????) (2. 16)

Et ensuite, on a de nouveau :

?????? = ????(???? ??-????).??????(????).(??+??????(????))?? ???????? ?? { ???? ?????? = ?? ???? ???????? = ????(???? ??-????).??????(????).(??+??????(??

(2. 17) ??))??

D'après l'équation (2. 6), on a : ????2 = ????2?????? = ??

????????2

????2 ???? ????2 ayant les mêmes expressions dans les deux solutions, on ne distinguera pas ici ces

deux solutions. On se retrouve dans les 2 cas avec :

????????????

?????? = ????(??????-??????)??????(????)(??+??????(????))?? (2. 18)

Or d'après l'équation (2. 3) , ????1 = ??1??2

??12

2

????2

??12 ayant la même expression dans les deux solutions mais à un signe près de même que ????2, on ne distinguera pas les deux solutions ici :

37