Chapitre 2- Procédure de synthèse d'une
cellule inductive
?? ????' ??????
?? ???????? = = (2. 4)
?????????? ??
??1' : représente la
fréquence de coupure du prototype passe-bas normalisé ; cette
dernière est égale à 1.
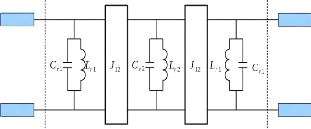
Figure 2. 18: Filtre passe-bande avec inverseurs
d'admittance idéaux
Finalement, Les valeurs des résonateurs (????1 - ????1)
et (????2 - ????2) sont données par les équations (2.
5) et (2. 6).
|
??????
??????
{
|
=
=
|
??????
|
(2.
|
5)
|
????
|
??????
??????
{
|
=
=
|
??????
|
(2. 6)
|
|
??.????
??
|
??.????
??
|
|
??????.????
|
??????.????
|
2.3.4.5 Implémentation des inverseurs d'admittances
idéaux
Dans cette étape, nous allons remplacer les inverseurs
d'admittances idéaux ??12 par leur circuit équivalent. Deux
solutions s'offrent à nous [28, p. 437], la structure en pi avec des
inductances et la structure en pi avec des capacités. Nous exploiterons
ces deux solutions.
a. Solution 1 : Structure en pi avec des inductances
Celle-ci est composée de deux inductances
négatives en parallèles séparées par une inductance
en série positive (cf. Figure 2. 19). La relation (2. 7) donne
la valeur de l'inverseur d'admittance en fonction de l'inductance et de la
pulsation ??0, associée à la fréquence de travail ??0 =
12,5??????. La Figure 2. 20 donne le circuit obtenu après
implémentation des inverseurs d'admittances idéaux.
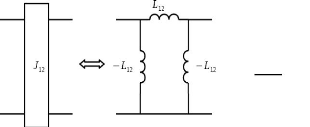
Avec :
??
?????? = (2. 7)
????·??????
33
Figure 2. 19 : Circuit équivalent d'un
inverseur d'admittance constituée d'une structure en pi avec des
inductances
Chapitre 2-Procédure de synthèse d'une
cellule inductive
En associant les admittances négatives
parallèles aux admittances des résonateurs parallèles, on
obtient le circuit de la Figure 2. 21. Les valeurs des
résonateurs parallèles (??1" -
??1") et (??2" -
??2") sont données par l'équation (2.8)
respectivement (2.9).
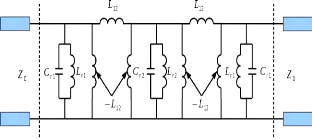
Figure 2. 20: Filtre passe-bande d'ordre 3
constitué de résonateurs parallèles et de deux structures
en pi avec des selfs
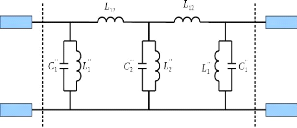
Figure 2. 21: Filtre passe-bande constitué
de 3 résonateurs parallèles séparés par deux
inductances
???? " = ?????? ???? " = ??????
{ ???? " = ??????\\(-??????) = ??????.?????? (2.
8) et { (2. 9)
???? " = (-??????)\\??????\\(-??????) = ??????.??????
??????-?????? ??????-????????
b. Solution 2 : Structure en pi avec des capacités
Cette structure est constituée de deux capacités
parallèles négatives séparées par une
capacité série positive (cf. Figure 2. 22). L'inverseur
d'admittance est exprimé ici en fonction de la capacité et de
??0 (équation (2. 10)). Le circuit équivalent obtenue
est illustré sur la Figure 2. 23.
|
Avec :
??????= ????· ?????? (2. 10)
|
34
Figure 2. 22: Circuit équivalent d'un
inverseur d'admittance constituée d'une structure en pi avec des
capacités
Comme pour la solution 1, on associe les capacités
négatives parallèles aux capacités positives des
résonateurs. On arrive au circuit de la Figure 2. 24, les
résonateurs parallèles (??1" -
??1") et (??2" -
??2") sont obtenue en appliquant les équations (2.
11) et (2. 12).
35
| 


