Synthèse de cellules unitaires de réseaux réflecteurs basée sur des techniques de synthèse de filtres

Chapitre 2- Procédure de synthèse d'une cellule inductive

???11(° /GHz)	??11(??0) (°)	P?? (d??) ??????	???? P?? (GHz)	??1^P?? (GHz)	??2 ^P?? (GHz)
-30	20	0,1834	13,782	8,758	21,688
-30	-20	0,1834	11,218	7,749	16,24

Tableau 2. 2: Valeurs des paramètres de la réponse du prototype passe-bande

2.3.4 Etapes de la synthèse du quadripôle équivalent

Dans cette section, nous allons synthétiser le circuit équivalent de la cellule inductive de Phoenix d'ordre 2 (cf. Figure 2. 10) à l'aide du prototype de filtre passe-bande d'ordre 3 (cf. Figure 2. 11) et en utilisant les techniques classiques de filtrage puis nous déterminerons les valeurs des éléments du circuit à l'aide des équations établies lors de la synthèse. Pour ce faire, nous procèderons par étape et à chaque étape de la synthèse correspondra une répartition différente des valeurs des éléments des circuits que nous déterminerons en fin de synthèse.

2.3.4.1 Définition du filtre passe-bas normalisé

En filtrage, la synthèse du filtre passe-bande d'ordre n (ou coupe-bande comme nous le verrons par la suite) commence par la définition du prototype de filtre passe-bas d'ordre n. La Figure 2. 14 illustre la configuration du filtre passe-bas normalisé d'ordre n=3.

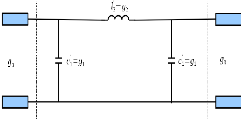
Figure 2. 14: Prototype du filtre passe-bas normalisé d'ordre n=3

Les coefficients 90, 91 et 92 , associés aux éléments localisés définissent la forme de la réponse du filtre passe-bande. Dans notre cas, nous souhaitons avoir une ondulation dans la bande passante (cf. Figure 2. 13) donc nous allons synthétiser un filtre de type Tchebychev.

Les valeurs des éléments du filtre passe-bas de Tchebychev peuvent dès lors être calculées [28, p. 99] en calculant

31

D'abord :

??ar

?? = ??n(??????h (17,37)

y = sinh ??

(2n)

[(2??-1)??]

a?? = sin 2?? , ?? = 1, 2, ... , n

???? =y²+sin²(^??_?^???), ?? = 1,2, ... ,n

Ensuite,

2a₁

y

9?? =

9₁ =

⁴????-1????

??= 1, 2,...,n

????-1????-1

9??+1 = 1 ????ur n im??air

= ??????h² (^??₄) ????ur n ??air

Chapitre 2-Procédure de synthèse d'une cellule inductive

2.3.4.2 Dénormalisation en impédance

En utilisant Z0 = 120ff impédance de l'air (milieu d'arrivée de l'onde incidente) comme impédance de référence, on obtient le circuit de la Figure 2. 15 suivante :

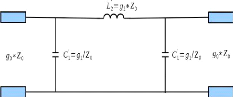
Figure 2. 15: Filtre passe-bas dénormalisé

2.3.4.3 Introduction des inverseurs d'admittances idéaux

Un inverseur d'admittance idéal, tel que défini ici, est la représentation de l'admittance elle-même [28, pp. 144-145], c'est-à-dire qu'il fonctionne comme une ligne quart-d'onde d'admittance caractéristique J à toutes les fréquences. Ainsi, pour avoir les équations de conception de certains filtre passe-bande ou coupe-bande, il est souhaitable de convertir le prototype passe-bas d'ordre n=3 de la Figure 2. 15 en utilisant uniquement des capacités parallèles _(Ca1 et _Ca2). Cela peut être fait à l'aide des inverseurs d'admittances idéaux (identiques dans notre cas J12) et on obtient le filtre passe-bas de la Figure 2. 16.

32

Figure 2. 16: Filtre passe-bas avec inverseurs d'admittances idéaux

L'équation (2. 3) donne la relation entre les différents paramètres du circuit. La démarche à suivre pour établir cette équation est donnée dans [28, pp. 146-149].

CajCa2

I12 = 8i82 (2. 3)

2.3.4.4 Transformation passe-bas/passe-bande

L'étape suivante consiste à transformer le filtre passe-bas avec des inverseurs d'admittances au filtre passe-bande avec des inverseurs d'admittances correspondant [28, pp. 428-429]. En appliquant la transformation illustrée sur la Figure 2. 17, on aboutit au filtre passe-bande d'ordre n=3 avec inverseurs d'admittances de la Figure 2. 18.

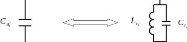
Figure 2. 17: Opération de transformation d'un filtre passe-bas en un filtre passe-bande

Les éléments des résonateurs parallèles (Lrj - C_ri)sont calculés en utilisant l'équation (2. 4).