3.1.3. Justification du choix
du modèle et de la méthode d'estimation
Plusieurs raisons ont motivé le choix de ce
modèle comme moyen de vérification d'hypothèses. En
premier lieu, il est en parfaite harmonie avec le cadre théorique de
notre travail. En effet, dans ce modèle les principales variables dont
les économistes considèrent comme les canaux de transmission des
dépenses publiques de l'éducation sur le plan macro
économique y figurent.
A côté de ces raisons, nous trouvons que c'est
un modèle simple à interpréter qui ne comporte qu'une
seule équation.
Il nous permet de voir, non seulement si les variables
explicatives influence les dépenses publiques de l'éducation,
mais aussi de saisir l'impact de chaque type de variable.
Pour ce qui concerne la méthode d'estimation, il
existe entre une panoplie de méthodes qui pourraient être
utilisée pour étudier les déterminants des dépenses
publiques de l'éducation. Parmi lesquelles, nous pouvons citer les tests
de corrélation, l'estimation d'un VAR, des relations de Co
intégration et des tests de causalité. Notre étude a suivi
le schéma de l'étude d'Arnaud BILEK sur l'économie
politique des déterminants des dépenses publiques
d'éducation en France, qui a estimé un modèle
économétrique par la méthode des moindres carrés
ordinaires.
Plusieurs raisons expliquent le choix et non un autre.
D'abord parce que les résultats fournis par la plupart de ces autres
modèles ne permettent pas d'approfondir l'analyse. Par exemple, les
tests de corrélation fournissent des informations sur le sens de la
relation entre les variables explicatives et expliquées, mais restent
muettes en ce qui a trait à la significativité statistique des
coefficients trouvés. Le test de causalité lui, informe sur la
manière dont des variables causent l'autre, mais ne permet pas de saisir
le sens de la causalité.
Contrairement à ces méthodes, l'estimation d'un
modèle économétrique montre le sens de la relation entre
la variable endogène et chacun des variables exogènes. Elle donne
le coefficient de chaque variable explicative, son degré de
significativité et permet de faire de nombreux tests, soit sur les
coefficients, soit sur le modèle proprement dit. Enfin, elle permet de
vérifier à quel pourcentage les variables exogènes
expliquent la variable d'intérêt. Cependant ; en vue
d'obtenir des résultats plus fiables, il importe de s'assurer de la
stationnarité des variables entrant dans le modèle.
3.1.4. Stationnarité des
variables
* Notion
Pour procéder à l'estimation de notre
modèle, nous allons au préalable nous rendre compte de la
stationnarité des variables à utiliser. Ceci est
nécessaire car les variables peuvent bien concerner l'espérance
que les moments de second ordre. Depuis Nelson et Plosser, les cas de non
stationnarité en moyenne sont analysés à partir de deux
types de processus : processus TS (Trend Stationnary) qui
représente le processus caractérisés par non
stationnarité de nature déterministe et processus Ds (Difference
stationnary) qui représente les processus dont la non
stationnarité est de nature stochastique.
Dans le premier cas, les données sont marquées
par une tendance générale. Il sied alors d'introduire un Trend ou
une Tendance générale dans le modèle. En présence
du second cas, si les ordres d'intégration des variables sont
différents, il faut les différencier en vue de les rendre
stationnaires.
Or, mettre en relation des variables dont les ordres
d'intégration sont différents, sans les rendre stationnaires, ne
peut que conduire à des fausses régressions ou régressions
fallacieuses.
En effet, les processus Ts et DS sont
caractérisés par des comportements très différents
et il convient de les distinguer suite à un choc. Un processus Ts
revient à son niveau pré-choc, alors qu'un processus Ds n'y
revient jamais. On comprend dès lors également que, d'un point de
vue économétrique, l'identification et la caractérisation
du non stationnarité sont tout aussi fondamentales. Pour ce faire, nous
allons utiliser le test de Diskey-Fuller (DF) et le test de Dickey - Fuller
Augmenté (ADF).
* Procédure et application du test de
stationnarité Dicky et Fuller considèrent trois modèles de
base pour la série Xt, t = 1, 2, 3, ... T :
1. Modèle [1] : modèle sans constante ni
Tendance déterministe : 
2. Modèle [2] : modèle avec constate sans
tendance déterministe : 
3. Modèle [3] : modèle avec constante et
tendance déterministe : 
Dans chacun des trois modèles, on suppose que  est un bruit blanc :  , L est l'opérateur retard ; xt est la variable
dont on teste la stationnaité ;  , M, dont des paramètres.
Si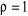 , cela signifie qu'une des racines du polynôme retard est
égale à 1. On dit alors qu'on est en présence d'une racine
unitaire. En d'autres termes, xt est un processus non stationnaire
et le non stationnarité est de nature stochastique (processus Ds). On
teste l'hypothèse nulle de racine unitaire (xt est
intégré d'ordre 1, c'est-à-dire non stationaire) contre
l'hypothèse alternative d'absence de racine unitaire (xt est
intégrée d'ordre 0), c'est-à-dire stationnaire).
En pratique, on estime les modèles sous la forme
suivante :
1. Modèle [1] : 
2. Modèle [2] : 
3. Modèle [3]: 
Avec pour chaque modèle,  . On teste alors l'hypothèse nulle  (non stationnarité) contre l'hypothèse alternative  (stationnarité) en se référant aux valeurs
tabulées par Fuller et Dickey. Dans la mesure où les valeurs
critiques sont négatives. La règle de décision est la
suivante : si la valeur calculée de t-statistique associée
à est inférieur à la valeur critique, on rejette
l'hypothèse nulle de non stationnarité. Si la valeur
calculée de la t-statistique associé à  est supérieure à la valeur critique, on accepte
l'hypothèse nulle de non stationnarité.
Il est fondamental de noter que l'on n'effectue pas le test
sur les trois modèles. Il convient en effet d'appliquer le test de
Dickey -Fuller sur un seul des trois modèles. En pratique, on adopte une
stratégie séquentielle en trois étapes :
Etape I : On commence par appliquer le
test sur le modèle 3. On peut aboutir à deux
résultats :
· Si la tendance n'est pas significative, on passe au
modèle 2.
· Si la tendance est significative, on teste
l'hypothèse nulle de racine unitaire :
1. Si n'est pas significativement différent de 0, Xt est
non stationnaire. Dans ce cas, il faut la différencier et recommencer la
procédure sur la série en différence première.
2. si  est significativement différent de 0, Xt est
stationnaire. Dans ce cas, la procédure s'arrête et l'on peut
directement travailler sur Xt.
Etape II. Cette étape ne doit
être appliquée que si la tendance dans le modèle
précédent n'est pas significative, on estime le modèle
2.
· Si la constante n'est pas significative, on passe au
modèle 1.
· Si la constante est significative, on teste
l'hypothèse nulle de racine unitaire :
1. Si  n'est pas significativement différent de 0, Xt est
non stationnaire. Dans ce cas, il faut la différencier et recommencer la
procédure sur la série en différence première.
2. Si  est significativement différent de 0, Xt est
stationnaire. Dans ce cas, la procédure s'arrête et l'on peut
directement travailler sur Xt
Etape III. Cette étape ne doit
être appliquée que si la constante dans le modèle
précédent n'est pas significative. On estime le modèle
1 :
1. Si n'est pas significativement différent de 0, Xt est
non stationnaire. Dans ce cas, il faut la différencier et recommencer la
procédure sur la série en différence première.
2. Si  est significativement différent de 0, Xt est
stationnaire. Dans ce cas, la procédure s'arrête et l'on peut
directement travailler sur Xt.
Plus précisément et de façon
schématique, voici l'organigramme de la succession de ces
différentes étapes.
Figure n°2: Test de stationnarité des
séries
Estimation Modèle 3
Différencier la série
 est-il significatif ?
Estimation Modèle 2
 est-il significatif ?
Différencier la série
 est-il significatif ?
Estimation Modèle 1
Série stationnaire avec tendance et constante
 est-il significatif ?
Série stationnaire sans tendance ni constante
 est-il significatif ?
Série stationnaire sans tendance mais avec constante
Non
Oui
Non
Oui
Non Oui Non
Oui
Non
Oui
Source : Dr. BOFOYA, Econométrie, cours inédit
à l'UNIGOM, L1 FSEG, 2009
Les variables sur lesquelles vont porter ces tests sont les
suivantes :
X1 : le logarithme du produit intérieur brut par
habitant
X2 : le logarithme du taux d'alphabétisation
X3 : le logarithme de la masse monétaire
X4 : le logarithme de l'inflation
Y : le logarithme des dépenses publiques de
l'éducation.
Après avoir effectué le test de racine unitaire
(ADF) à ces différentes variables, on peut alors
déterminer l'ordre d'intégration de chacune d'entre elles. Les
résultats obtenus sont récapitulés dans le tableau
suivant :
Tableau n°3: Test de racine unitaire
des variables du modèle
|
Variables
|
Modèle utilisé
|
ADF test statistique
|
Valeurs critiques
|
Ordres d'intégration
|
|
Y (log Dép. Educ)
|
Avec constante
|
-4,513669
|
1% ? -3,6852
5% ? -2,9705
10% ? -2,6242
|
I (0)
|
|
X1
|
Sans constante, ni tendance
|
-2,882565
|
VOIR ANNEXE
|
I (1)
|
|
X2
|
Sans constante, ni tendance
|
-3,559176
|
I (1)
|
|
X3
|
Sans constante, ni tendance
|
-5,179417
|
I (1)
|
|
X4
|
Sans constante, ni tendance
|
|
I (1)
|
Source : Nos résultats avec le
logiciel Eviews 3.1
Pour ce qui concerne les variables du modèle, le
tableau montre que l'une d'entre elles est stationnaire à niveau.
Il s'agit des dépenses publiques de l'éducation,
les autres variables sont stationnaire en différence première.
A ce stade, on peut spécifier notre modèle comme
suit :
Equation : Lo (Y) =
â0+log(x1)+â2log(x2)+â3log(x3)+â4log(x4)
+ 
| 
