6.3 Persistance des chaInes trophiques a deux
echelons
Pour le modèle R-M, le paramètre de croissance
r est intéressant en tant que facteur supplémentaire
d'enrichissement du milieu. Malgré l'indépendance des
bi-
RéSUlTaTS ET DISCUSSION

1
a
0.5
0 0.4
b
0.2
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Capacité limite du milieu (K)

4
c
2
0
2
d
1
0
0 0.5 1 1.5 2 2.5
Xr en mg.mL-1
FIG. 8 ~ Comparaison des diagrammes de bifurcation du
modèle de R-M : (a) et (b), avec r = 1, et du modèle
DEBf: (c) et (d) avec h ÿ = 0, 1
furcations de r, l'action de ce
paramètre se situe sur la quantité de biomasses a
l'équilibre et sur la vitesse d'ouverture du cycle limite
lorsque K augmente. En effet, dans le domaine d'apparition du
cycle limite, plus r sera petit plus le minimum de biomasse de
prédateurs sera faible pour une même valeur de K. Cette
démarche abouti a un découpage de l'espace des paramètres
en quatre zones suivant si : les deux espèces sont sous le seuil, seule
la proie est sous le seuil, seul le prédateur est sous le seuil ou
aucune des deux espèces n'est sous le seuil (Fig. 9).
Pour le modèle DEBf, il a été possible
d'utiliser des seuils naturels (Fig. 10). Le seuil correspond alors a la
biomasse représentée par un seul individu dans le chemostat.
Toutefois, pour observer l'effet d'éventuelles perturbations sur le
milieu, un seuil beaucoup plus important a été choisi
arbitrairement. Avec l'utilisation des seuils naturels, le modèle a deux
échelons trophiques présente une large zone de coexistence pour
une concentration en glucose supérieure a 0, 2
mg.mL-1 et pour un taux de dilution
inférieur a 0, 22 h-1. Dans la version a
trois échelons, on observe la même répartition
imbriquée :
- pour une concentration en glucose faible ou un fort taux de
dilution, seule la proie survie
- pour une concentration en glucose plus importante ou un taux
de dilution moyen il y aura coexistence de la proie et du prédateur
0.2 0.4 0.6 0.8 1
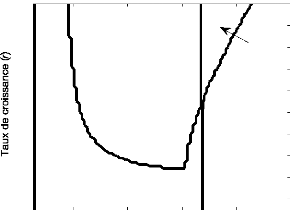
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
Survie de la proie
uniquement
Survie de la
proie et
du prédateur
Survie ni de
la proie,
ni du
prédateur
Disparition
de la proie
entraine celle
du
prédateur
Capacité limite du milieu (K)
FIG. 9 - Diagramme de survie des espèces du modèle
R-M en fonction de K et de r pour un seuil de 0,05.
- pour une concentration en glucose suffisante ou un faible taux
de dilution la coexistence des trois espèces sera possible
Dans un premier temps, l'enrichissement permet bien
d'accroItre le nombre d'espèces de la chalne trophique mais cette
possibilité est fortement contrainte par le taux de dilution. Avec ce
seuil très bas, les oscillations ne provoquent pas de changement dans
les zones de survie.
| 


