TROISIÈME CHAPITRE : CADRE MÉTHODOLOGIQUE
Dans cette partie de notre travail, nous présenterons
les différentes stratégies choisies pour atteindre l'objectif
assigné à cette recherche. Il s'agit de la population
d'étude, l'échantillon d'étude, les méthodes et
techniques de récolte des données, le mode de
dépouillement, la technique de traitement des données ainsi que
les difficultés rencontrées sur terrain pendant la
réalisation de cet outil scientifique.
3.1.
Population d'étude
C'est l'ensemble d'éléments parmi lesquels on
aurait pu choisir un échantillon, c'est-à-dire l'ensemble
d'éléments qui possèdent les caractéristiques qu'on
veut observer (BERTLIER, N. cité par Jean Paul MAJORO 2008, p.55).
Selon R. MUCCHIELLI (1941, p.26), la population
d'étude est un ensemble des groupes concernés par les objectifs
de l'enquête.
Quant à ce qui concerne cette recherche, les agents de
la REGIDESO /Bukavu, constituent notre population d'étude.
Signalons qu'une population peut être finie ou infinie.
Elle est finie lorsque le nombre est bien connu par le chercheur,
c'est-à-dire le nombre est bien déterminé. Elle sera alors
infinie lorsque le nombre n'est pas connu par le chercheur, c'est-à-dire
illimité.
Pour ce qui est de cette recherche, signalons que notre
population est finie parce qu'elle est constituée de 130 personnes.
3.2.
Échantillon d'étude
Selon DEKELE(1991, P.112), échantillonner c'est choisir
un nombre limité d'individus dont on va observer et mesurer un
caractère dans le but de tirer des conclusions applicables à la
population entière dans laquelle le choix a été fait ou
à laquelle on s'intéresse. Le mode de constitution de
l'échantillon est d'une importance capitale, son choix est fondamental,
car il conditionnera, en particulier, la validité d'induction.
La REGIDESO possède un grand nombre d'agents de
façon que nous ne pouvons pas les considérer tous comme
échantillon. La population mère est de 130 agents.
Selon GHIGLIONE, L. et MATALON, T. cité par J. d'Amour
NIZEYUMUKIZA (op.cit. p.54), étudier exhaustivement une population ou
étudier tous ses membres est pratiquement impossible, car cet exercice
est long et couteux voir même inutile ; il faut interroger un nombre
restreint de personnes à condition qu'elles aient été
correctement choisies, peut apporter autant d'information, à une
certaine erreur près, erreur calculable, et qu'on peut rendre
suffisamment fiable.
De ce fait, choisir un nombre restreint de personnes au sein
de la population parente, c'est échantillonner qui, d'après G. De
LANDSHEERE cité par idem. (op.cit.), signifie choisir un nombre
limité d'individus, d'objets ou d'événements dont
l'observation permet de tirer des conclusions applicables à la
population entière à l'intérieur de laquelle le choix a
été fait.
Ainsi, comme il n'est pas toujours possible voire même
nécessaire d'étudier toute la population pour bien la
connaître, le chercheur se contente de recueillir les informations
nécessaires sur un échantillon. Par conséquent, les
résultats obtenus auprès d'un sous-groupe doivent
nécessairement refléter l'opinion de toute la population.
De notre part nous avons fait recours à
l'échantillonnage stratifié, qui d'après Z .MUKE
(2011, p.123), consiste d'abord à subdiviser la population cible en
sous-groupes relativement homogènes ou "strates", puis à tirer de
façon aléatoire un échantillon dans chaque
strate. Alors, l'ensemble des échantillons ainsi choisis constitue
l'échantillon final qui sera l'objet de l'étude.
Ainsi, pour choisir l'échantillon qui fait l'objet
d'étude, afin de nous permettre d'adresser les questionnaires à
nos enquêtés, nous nous sommes servi de l'échantillon
stratifié pondéré. Sachant que la population
d'étude est représentée par 130 employés, la taille
de l'échantillon (niveau de confiance de : 95 ; niveau de
précision de : #177; 5 %) est de 97 personnes (idem.
op.cit. p.407).
En s'appuyant sur la théorie de L.D'HAINAUT cité
par idem. (op.cit. p.124), qui souligne en disant que l'on peut quand on
constitue un échantillon, s'assurer que les strates de la population
sont bien représentés dans l'échantillon ;
c'est-à-dire qu'il faut que les effectifs des strates de
l'échantillon soient proportionnels aux effectifs des strates de la
population.
Alors, la formule est la suivante :
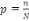 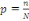 Où : Où :
Ø P= Proportion ;
Ø n= Effectif de l'échantillon et
Ø N= Effectif total.
Partant de cette formule, nous avons ainsi :
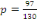 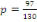 = 0.75 = 0.75
Tableau n°1 : La taille de
l'échantillon
|
N°
|
STRATES
|
NOMBRE DES EMPLOYÉS
|
ÉCHANTILLON
|
|
01
02
03
04
05
06
07
08
09
|
Secrétariat Dp.
Centre Médical
Centre Informatique
Contrôle de Gestion
Administration et Finance
Service Commercial
Service Production
Service Distribution
Logistique
|
2
8
2
3
10
60
16
15
14
|
2×0,75=1
8×0,75=6
2×0,75=1
3×0,75=2
10×0,75=8
60×0,75=45
16×0,75=12
15×0,75=11
14×0 ,75=11
|
|
TOTAL
|
|
130
|
97
|
Source : nos
enquêtes
Partant des données de ce tableau, nous constatons que
le Secrétariat Dp. et le Centre Informatique ont le même nombre
réduit d'agents 2 et c'est pourquoi ils ont un nombre réduit de
l'échantillon 1 et le Service Commercial a le grand effectif des agents
60, c'est pourquoi il a aussi un grand nombre d'échantillon 45
agents.
| 


