![]()
CALCUL DES ELEMENTS D'UNE BETONNIERE
Partie 1 : Calcul de la chaîne
Données :
Puissance de moteur: 7,5 KW;
Nombre de tours 1500 tr/min ;
Rapport de transmission (chaîne)  ; ;
L'entraxe (Plateau) a = 350 mm;
II.1.1. Choix de la chaîne
Moteur
Chaîne
Arbre (A)
Roue N2
Pignon N1
Chaîne
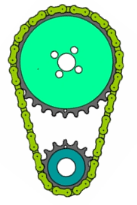

Fig.II.1
Calculons d'abord la puissance effective d'une transmission
par chaîne. [ 1 ]
On sait que :
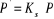
 : Puissance de moteur. : Puissance de moteur.
 : Puissance effective. : Puissance effective.
 : Facteur de service. : Facteur de service.
On prend :  (voir Tab.1
Annexe) (voir Tab.1
Annexe)
On obtient :
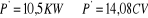
En consultant l'abaque ( Fig.1 Annexe) on constat qu'on a le
choix entre :
- Une chaîne simple 50-1 (Tab.2 Annexe) pas = 0,625 po
 pas =
15,875mm pas =
15,875mm
- Une chaîne double 40-2 ( Tab.3 Annexe) pas = 0,5 po
 pas =
12,7mm pas =
12,7mm
- Une chaîne triple 40-3 pas = 0,5 po  pas = 12,7
mm pas = 12,7
mm
)
II.1.2. Détermination du Nombre de dents du pignon
et de la roue
Calculons d'abord le nombre de tours du la roue N2
Soit :
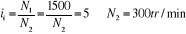
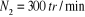
Puisque  ce rapport
est satisfait pour prend Z1 = 21 et Z2 = 105 dents ce rapport
est satisfait pour prend Z1 = 21 et Z2 = 105 dents
II.1.3. Calcul de la puissance nette
On sait que :
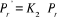
 : Puissance nette. : Puissance nette.
 : Facteur tenant compte du nombre de rangée de la
chaîne. : Facteur tenant compte du nombre de rangée de la
chaîne.
 : Puissance nominale. : Puissance nominale.
Pour Z1 = 21 dents, on obtient les valeur de  présentées au tableau ci-dessous:
présentées au tableau ci-dessous:
|
Type de chaîne
|
K2(Tab.4 Annexe)
|
Pr(CV)
|
Pr'(CV)
|
Pr'(KW)
|
|
Chaîne 40-3
|
2,5
|
9.90
|
24,75
|
18,456
|
|
Chaîne 40-2
|
1,7
|
9,90
|
16,83
|
12,550
|
|
Chaîne 50-1
|
1
|
17,85
|
17,85
|
13,310
|
On constate que les deux chaînes 40-2 et 50-1 satisfont
à la condition 
La chaîne 40-2 sera mieux exploitée ( la valeur
de  étant plus proche de la valeur désire de
étant plus proche de la valeur désire de  ), c'est
elle qu'il faudra choisir (même si, fort probablement une étude
économique détaillée ferait opter pour la chaîne
50-1) ), c'est
elle qu'il faudra choisir (même si, fort probablement une étude
économique détaillée ferait opter pour la chaîne
50-1)
II.1.4. Calcul de la longueur de la chaîne
La longueur de la chaîne en nombre de maillons est
donnée par l'équation:
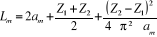
 : Longueur
de la chaîne, en nombre de maillons. : Longueur
de la chaîne, en nombre de maillons.
 : Entraxe en nombre de maillons. : Entraxe en nombre de maillons.
Et on a:
 = =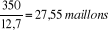
 : Entraxe. : Entraxe.
 : Pas primitif de la chaîne, du pignon et de la roue. : Pas primitif de la chaîne, du pignon et de la roue.
Donc:
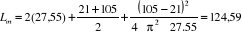
On prend:

et la longueur de la chaîne est
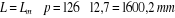
 : Pas primitif de la chaîne. : Pas primitif de la chaîne.
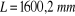
II.1.5. Détermination de l'entraxe
A l'aide de l'équation suivant on calcule la valeur
modifiée de  soit : soit :
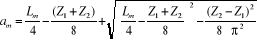
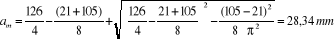
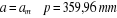
On prend :
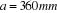
II.1.6 Vérification de l'angle d'enroulement 
Les équations suivantes permettent de calculer les
diamètres primitifs de la roue et du pignon

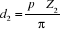
Donc: 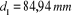
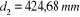
On sait que :
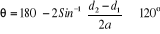
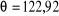
II.1.7 efforts appliques sur une chaîne
Toute fois il faut examiner la possibilité de bris de
la chaîne choisie.
On a :
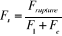
 : Facteur de sécurité. : Facteur de sécurité.
 : La charge minimale de rupture déterminer pour chaque
chaîne. : La charge minimale de rupture déterminer pour chaque
chaîne.
 : Tension utile due a la transmission de la puissance. : Tension utile due a la transmission de la puissance.
 : Tension due à la force centrifuge. : Tension due à la force centrifuge.
Et que :
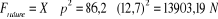
 Pour les
chaîne a rouleaux. Pour les
chaîne a rouleaux.
 : Pas primitif de la chaîne. : Pas primitif de la chaîne.
et : 
 : Vitesse de la chaîne, en m/s. : Vitesse de la chaîne, en m/s.
Ou : 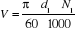
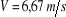
Donc: 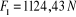
Et : 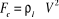
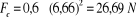
 (Voir
Tab.5 Annexe) (Voir
Tab.5 Annexe)
 : Masse
linéique. : Masse
linéique.
Donc : 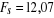
Finalement pour éviter la rupture de la chaîne,
il faut vérifier que l'inégalité suivant est satisfaite
:
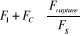
Il est donc clair que la chaîne est
sécurisée.
| 


