Chapitre IV
Développement des corrélations et
abaques
4.1 Corrélations
L'un des objectifs visés lors de la conception des
systèmes de refroidissement de composants électroniques, à
base de MCP, est la prévention de ces derniers de la surchauffe. Pour le
cas des systèmes de refroidissement actif, un tel objectif est atteint
en ayant recours à un mode de refroidissement par convection naturelle
et/ ou forcée à l'air ou à un liquide (eau ou liquide
diélectrique, tel que le FC 72, par exemple). Dans le cas d'un
système de refroidissement utilisant un MCP fonctionnant selon un mode
passif, la surchauffe peut se manifester après une certaine durée
de fonctionnement. L'efficacité de refroidissement est d'autant
élevée que cette durée est maximale et la fusion du MCP
est totale (f ~ 1). Ainsi, il serait pratique de développer des
corrélations et/ou des abaques permettant le calcul de la durée
de fonctionnement sécurisé et la fraction liquide au lieu du
Nombre de Nusselt moyen pour chaque source de chaleur. De tels abaques et
corrélations sont très utiles pour les concepteurs oeuvrant dans
le domaine du contrôle thermique des équipements
électroniques. Ils permettent de déterminer les paramètres
de contrôle correspondant à une durée de fonctionnement
sécurisé donnée.
La présente section expose la méthode
adoptée pour élaborer les corrélations exprimant la
durée adimensionnelle, ôfonc, et la fraction liquide,
f, en fonction des différents paramètres de
contrôle. Cette méthode est basée sur l'approche de
développement asymptotique qui consiste à développer la
solution d'un problème au voisinage d'une solution particulière,
appelée solution de référence. La procédure
détaillée d'une telle méthode est
rapportée par Balaji et Herwig [68]. Il est à
rappeler que les valeurs de référence des variables
indépendantes qui correspondent à la solution de
référence (ôfonc,réf = 0,1013 et
fréf = 0,868) sont données au Tableau 3.3. Les Figures
4.1.a et 4.1.b illustrent les variations respectives de ôfonc
et f en fonction des variables indépendantes
normalisées, ë i = 1,...8 ,
suivantes:
-
~~
Pour la durée, ôfonc:
0.6 i X1.6
(4.1)
0.07
, aR 1 LAÄ
A1 , ',2 A
Ra ref ref
2.8
[
[-1.17
ë3 = á s 0.154
ás , X,4 = Ec '
f
á s,ref Ec,ref
~ ~ ~
0.5 -0.95
E s ) A ) ác
LE s,ref ref A ref á c,ref
-
-
~
~
~
~
L
2.7 1.8
· = Ra Ä
Ra ref 2 Äref
· = [[ á s )-0.151[ ás = Ec
á s,ref á s,ref Ec,ref
2.7 -1.4
Pour la fraction liquide, f:
(4.2)
-
~á ~
c
, ë =
8
~ ~
~á ~
c,ref
0.15
0.5 11.05
= E s
A
ë5 E = [ ref =[Aref
s,ref
Il est clair, de ce qui précède, que les valeurs de
référence des variables susmentionnées sont:
- Pour la durée adimensionnelle, ôfonc
réf = 1, ë2, réf = 1, ë3, réf =
0,846, ë4, réf = 1, (4.3)
ë5, réf = 1, ë6, réf = 1, ë7,
réf = 1, ë8, réf = 1
- Pour la fraction liquide, f
ë1, réf = 1, ë2, réf = 1, ë3,
réf = 0,849, ë4, réf = 1, (4.4)
ë5, réf = 1, ë6, réf = 1, ë7,
réf = 1, ë8, réf = 1
ë1
ë7 ë8 ë4 ë2
ë3
ë5
ë6
0 0.5 1 1.5 2 2.5 3 3.5 4
ë
(a)
ë3
0.8
ë5
ë6
ë4
ë1
ë2
0 0.5 1 1.5 2 2.5 3
ë
0.2
ô fonc
1
f
0.15
ô fonc,ref
0.1
0.05
0.9
fref
0.7
ë7
ë8
(b)
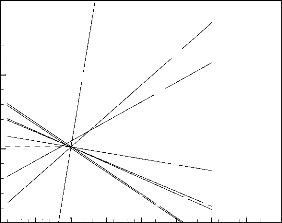
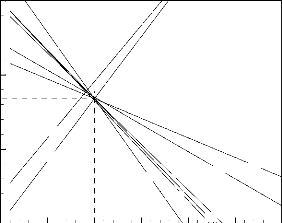
Figure 4.1: Variations de la
durée de fonctionnement sécurisé, ôfonc,
(a) et la fraction liquide,
f, (b) en fonction des variables indépendantes,
ë1, ....., ë8
Il ressort d'une simple analyse des figures
précédentes que la variation de ces deux solutions autour des
solutions de référence est linéaire. Ainsi, le
développement en série de Taylor, autour des solutions de
référence, permet d'écrire ôfonc et
f, comme suit:
ôfonc= ôfonc, réf + ~ (ë i -
ë i, réf) [? ôfonc/ ? ë i] ëi=ëi, réf
(4.5)
i = 1 , 8
f = f réf + ~ (ë
i - ë i, réf) [? f fonc/ ? ë i]
ëi=ëi, réf (4.6)
i = 1 ,8
Les dérivées partielles figurant dans les
expressions (4.5) et (4.6) sont les pentes des courbes linéaires des
Figures 4.1.a et 4.1.b. Par exemple, pour ôfonc, la
dérivée partielle ?ôfonc / ? ëi| ëi=ëi,
réf, est la pente de la courbe représentant la variation de
ôfonc en fonction de ëi, les autres variables
indépendantes, ë j(j ? i), étant constantes et égales
à leurs valeurs de référence. Cette pente est
déduite directement de la corrélation (3.1),
développée au chapitre précédent. Le même
raisonnement s'applique pour le calcul des autres dérivées
partielles. Ainsi, après substitutions des valeurs des
différentes dérivées partielles, les corrélations
suivantes on été déduites:
ôfonc = 0,1013 + 0,288 (ë1 - 1) - 0,02 (ë2 - 1) +
0,02645 (ë3 - 0,846) - 0,02113 (ë4 - 1)
+ 0,042 (ë5 - 1) - 0,008 (ë6 - 1) - 0,0311 (ë7 -
1) + 0,03202 (ë8 - 1) (4.7)
f = 0,868 - 0,135 (ë1 - 1) - 0,1314 (ë2 - 1) +
0,152 (ë3 - 0,849) - 0,1231 (ë4 - 1)
+ 0,168 (ë5 - 1) - 0,0528 (ë6 - 1) - 0,1787 (ë7 -
1) + 0,0732 (ë8 - 1) (4.8)
Les courbes de parité (Figure 4.2) relatives à
ôfonc et f montrent que les résultats de
simulation se comparent de manière satisfaisante à ceux obtenus
par les corrélations (4.7) et (4.8). L'écart maximal est de
l'ordre de 8 %.
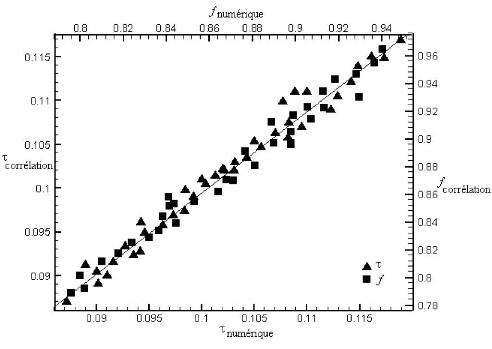
Figure 4.2: Courbes de parité pour
ôfonc et f.
|
|



