Etude des transferts de chaleur dans une enceinte confinant un matériau à changement de phase et chauffée par des sources de chaleur protubérantes sur une paroi conductrice verticale

4.2 Elaboration des abaques

Pour faciliter l'exploitation des corrélations (4.7) et (4.8), deux abaques, Abaque I et Abaque II, ont été élaborés. Pour une valeur de la durée adimensionnelle de fonctionnement sécurisé, ôfonc , on choisi le contour correspondant: c'est l'iso- durée sur l'Abaque I. Les

valeurs des huit paramètres de contrôle du puits de chaleur (A, E_s, E_c, A , , a_s , Ra, ~_c ) sont aussi déterminées, en faisant une projection orthogonale sur chaque coté de l'octogone. Connaissant les valeurs des huit paramètres de contrôle, la fraction liquide, f , est ainsi déduite de l'Abaque II.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9

a_c /a_c,ref

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9

Ra /Ra

á /á

s s,ref

ref

c c, ref

E /E

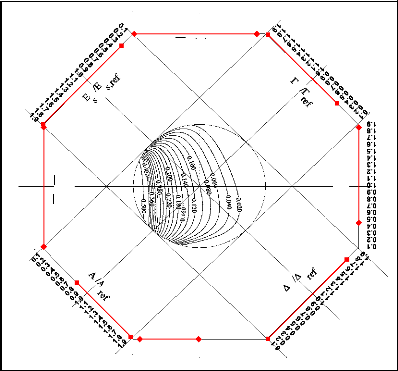
Abaque I: Durée adimensionnelle de fonctionnement sécurisé, ôfonc

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9

a_c /a_c,ref

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9

Ra /Ra

ref

E _c ^/E _{c, ref}

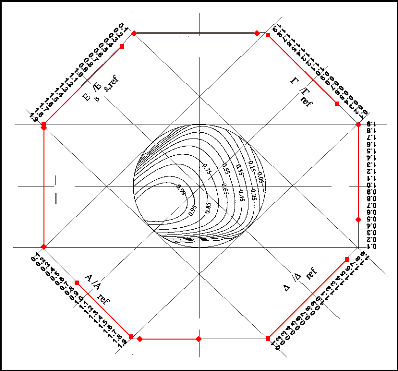
Abaque II: Fraction liquide, f

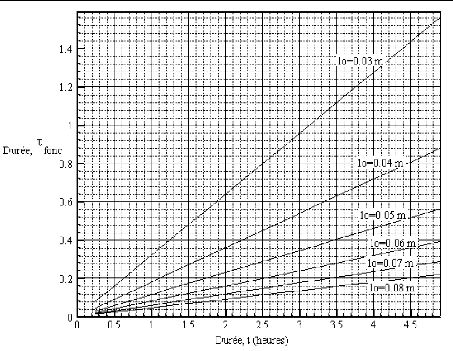
Abaque III: Durée adimensionnelle de fonctionnement sécurisé en fonction de la durée dimensionnelle de fonctionnement sécurisé pour différentes valeurs de l_o.

4.3 Exemple d'application

L'objectif est de faire fonctionner un puits de chaleur durant une période, t =90 minutes, durant laquelle la température maximale des trois composants électroniques doit être inférieure à la valeur critique, _Tcr, La puissance générée par unité de longueur par chacune des sources de chaleur est, Q'= 58,5 W/m. Quelles sont les valeurs des paramètres de contrôle permettant de réaliser un tel objectif ?

Un abaque supplémentaire a été élaboré pour éviter les calcules intermédiaires, il s'agit

de l'Abaque III donnant la durée adimensionnelle, _ôfonc , correspondant à la durée réelle pour

différentes valeurs du paramètre, l_o (représentant la masse du MCP).

Pour l_o=0,062 m, cette durée est ôfonc = 0,105. Ainsi, l' iso- durée sur l'Abaque I, est celui

correspondant à ôfonc =0,105.

En remarquant que	Ra Q' =	et que Q' =58,5 W/m, Q 'ref =60 W/m, le rapport
	Ra Q' ref ref

Ra Q'

= = 0,975. Sur l'Abaque I on obtient un point d'intersection entre la normale sur

Ra Q'

ref ref

le coté de l'octogone

= 0,975, et le contour ôfonc =0,105. A partir de ce point, les valeurs

Ra

Ra ref

des autres paramètres de contrôle sont déduites par des projections normales sur les côtés correspondantes de l'octogone. Ainsi, on obtient les valeurs suivantes, pour les différents paramètres de contrôle:

0.0161 et Ä f

Äô fonc

ô fonc

0,0023

Ra/ Ra réf = 0,975 E_s E_s réf = 1,1

Ä/ Ä réf = 0,62 / réf = 1,4

á s / á s, réf = 0,48 A/ A _réf =1,5

E_c/ Ec, réf =0,65 á c / á c, réf =1,35

La fraction liquide, f, est déduite directement de l'Abaque II, de même échelle que l'abaque I. Les huit valeurs des paramètres de contrôle, déterminées sur l'Abaque I, doivent être positionnées sur les cotés correspondants de l'Abaque II. Le point d'intersection des droites verticales issues des cotés de l'octogone de l'Abaque II et passant par les valeurs des paramètres de contrôle, donne, f = 0,85.

La vérification par les expressions (4.7) et (4.8) a donné:

ôfonc = 0,106723 et f = 0,852

Abaques: ô fonc = 0,105 et f = 0,85