3.4.8 Effet de la diffusivité thermique
adimensionnelle des sources de chaleur, á c /á c,ref
L'effet du rapport des diffusivités thermiques
adimensionnelles des sources de chaleur, á c /á
c,ref, sur la variation temporelle de la température maximale
adimensionnelle des sources
de chaleur, Omax , et la fraction
liquide, f, est illustré à la Figure 3.37. Les
simulations
numériques ont été effectuées en
considérant la marge de variation du rapport á c
/á c,ref: 0,1 -
20. Comme il est montré sur cette figure, durant la
première phase du processus de fusion,
caractérisée par
la prédominance de la conduction thermique, plus le rapport á
c /á c,ref est
élevé, plus l'augmentation de la
température maximale adimensionnelle des sources de
chaleur est
lente. Ceci est dû au fait que l'accroissement de la diffusivité
thermique
adimensionnelle des sources de chaleur augmente leur
habilité à uniformiser leur température et à
diffuser plus facilement la chaleur générée en leur sein
au lieu de la stocker sous forme sensible; favorisant ainsi le transfert de
chaleur vers la plaque conductrice et la couche du MCP liquide entourant les
faces des sources de chaleur. Ces constatations sont en accord avec les
résultats obtenus par Jaluria et al. [67], lors de l'étude du
refroidissement d'un composant électronique enfermé dans une
enceinte rectangulaire confinant l'air comme fluide de refroidissement. Le
système atteint rapidement le régime quasi- stationnaire
(plateau, Figure 3.37) pour les faibles valeurs du rapport á
c /á c,ref, à l'encontre du cas avec des
sources de
chaleur de diffusivité thermique adimensionnelle
élevée, pour lequel la première phase du processus de
fusion, dominée par la conduction thermique, persiste plus longtemps.
ô
èmax
0.035
0.025
0.015
0.005
0.03
0.02
0.01
X
0 0.02 0.04 0.06 0.08 0.1 0.12
Température limite adimensionnelle, cr
è
X
X
X X
X X X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
á /á
__
c
0.1
0.5
20
1
10
c,ref
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
f
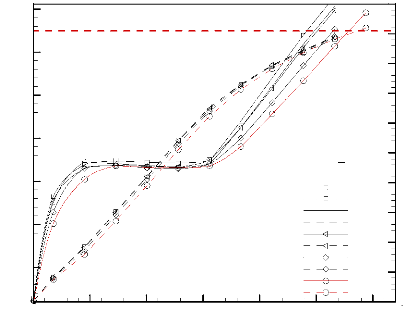
Figure 3.37: Effet du rapport des
diffusivités thermiques adimensionnelles, á c
/á c,ref, sur
l'évolution temporelle de la température maximale
adimensionnelle des sources de chaleur et la fraction liquide.
Une autre constatation qui peut être
dégagée de l'analyse de la Figure 3.37 est qu'en régime
quasi- stationnaire, la température maximale adimensionnelle des sources
de chaleur la plus basse est enregistrée pour le cas des sources de
chaleur ayant une diffusivité thermique adimensionnelle
élevée. La température maximale adimensionnelle,
°max , atteinte par les
sources de chaleur, en régime quasi- stationnaire, est
égale à 0,017 (Tmax= 56.33 °C) pour
á
c /á c,ref = 0,1 et 0,016 (Tmax= 55,13 °C)
pour á c /á c,ref= 20. Quant aux fractions
liquides,
obtenues à la fin du processus de fusion ( O
max = O cr ), elles sont, respectivement,
0,84 et 0,9.

L'effet du rapport á c /á c,ref sur le
profil de température adimensionnelle de la plaque
conductrice ( Es
X= - ) est donné à la Figure 3.38. A l'exception du
régime quasi stationnaire
2
( ô = 0 ,051), pour lequel le profil de
température est quasi indépendant du rapport á
c /á c,ref ,
les deux autres régimes ( ô = 0,007 et ô
=0,0844) sont tels que l'accroissement du rapport
á c
/á c,ref entraîne une baisse de température non
pas seulement des sources de chaleur mais
aussi celle de la plaque conductrice. En effet, comme il a
été expliqué précédemment,
l'augmentation
de ác/ác,ref rend les sources de chaleur plus habiles
à diffuser la chaleur au
lieu d'en stocker, ce qui cause une intensification du
transfert de chaleur et par conséquent une baisse de la
température adimensionnelle des sources de chaleur et de la plaque
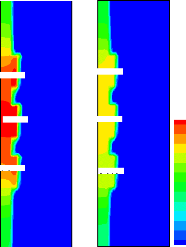
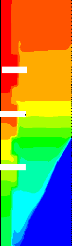
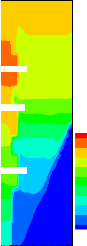
conductrice. Ce résultat est aussi confirmé à la Figure
3.39, illustrant le champ de température, la position et la forme du
front de fusion aux instants ô = 0,007, ô = 0
,051 et ô =0.0844, représentant les trois phases
du processus de fusion. On remarque bien les températures
élevées dans le cas où á c /á
c,ref =0,1.

__ __
á /á
c
ô=0,007
0,1 1
20
c,ref
|
2
1.5
Y 1
0.5
0
2
1.5
Y
1
0.5
0
2
1.5
Y 1
0.5
|
0.01 0.015 0.02 0.025 0.03
ô=0,051
0.01 0.015 0.02 0.025 0.03

ô=0,0844
0.01 0.015 0.02 0.025 0.03
è
Figure 3.38: Effet du rapport
ác/ác,ref sur le profil de température
adimensionnelle au sein de la plaque conductrice en Es
X= - .
2
è
0.012 0.011 0.010 0.009 0.008 0.007 0.006 0.005 0.004 0.003
0.002 0.001 0.000
ô = 0,007
0.0120
0.0120
0.0111
0.0101
0.0091
0.0091
á c /á c,ref = 0,1 f = 0,085
á c /á c,ref = 20 f = 0,075
ô = 0,051 ô = 0,0844
0.0133
0.0162
0.0157
0.0133
è
0.017 0.017 0.016 0.015 0.012 0.010 0.007 0.004 0.001
0.0196
0.0221
0.0147
è
0.025 0.022 0.020 0.017 0.015 0.012 0.010 0.007 0.005 0.000
0.0245
0.0245
0.0172
á c /á c,ref = 0, 1 f = 0,53
á c /á c,ref = 20 f = 0,51 á
c /á c,ref= 0,1 f = 0,79 á c /
á c,ref= 20 f = 0,78
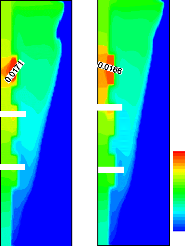
Figure 3.39: Effet du rapport á c /
á c,ref sur le champ thermique.
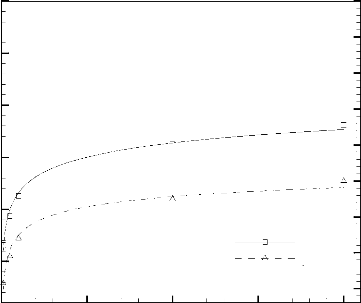
La durée adimensionnelle de fonctionnement
sécurisée, ôfonc , et la fraction liquide,
f, sont données à la Figure 3.40 pour différents
rapports á c /á c,ref. Il ressort de
l'analyse de cette
figure que la durée ôfonc et la fraction
liquide, f, augmentent lorsque á c /á
c,ref s'accroît.
Toutefois, pour ác/ác,ref > 10, la durée,
ôfonc , et la fraction liquide, f, subissent une
légère augmentation.
0.12
0.115
0.11
ô
fonc
0.105
0.1
0.095
1
0.98
0.96
0.94
f
0.92
0.9
0.88
0.86
0.84
0 5 10 15 20
_
á /á
c c,ref
f
ô
fonc
Figure 3.40: Durée de fonctionnement
sécurisé, ôfonc , et fraction liquide, f,
en fonction du
rapport á c / á c,ref.
En adoptant la même procédure de
développement des corrélations que dans le cas des autres
paramètres de contrôle, il ressort de la Figure 3.40 que les
corrélations donnant la
durée adimensionnelle, ôfonc , et la
fraction liquide, f, sont:
|
- 0 07
, - 0 15
,
( '
á ~ '
á
c c
ô = 0,13363 - 0 0320248
, , = 0,9430688 - 0 0731999
f ,
fonc ~ á ~ ~ á
~
~ )
c ref
, ~
c ref
,
|
(3.9)
|
avec 0,1 < á c /á
c,ref < 20
Un accord satisfaisant est obtenu entre les résultats
numériques et ceux de la corrélation (3.9). La variation maximale
est de l'ordre de 1 %.
| 


