3.4.5 Effet de l'épaisseur adimensionnelle du
substrat, Es
Dans cette section, on étudie l'effet de
l'épaisseur adimensionnelle de la plaque conductrice (substrat),
Es, sur le refroidissement des sources de chaleur. Les simulations
numériques ont été effectuées en variant le
paramètre Es /Es,ref dans la plage: 0,4 - 2.
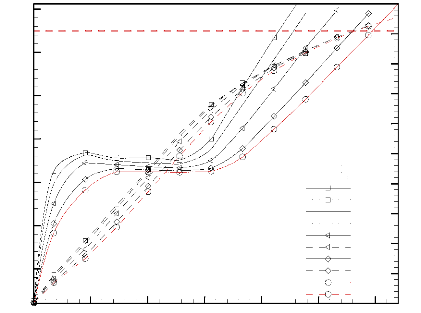
L'effet de ce paramètre sur Omax et
f est illustré à la Figure 3.24. L'analyse de cette
figure montre que la température maximale adimensionnelle la plus
élevée et la durée adimensionnelle de fonctionnement
sécurisé la plus courte sont obtenues pour le cas d'une plaque
conductrice (substrat) de faible épaisseur, à cause de son
inertie thermique relativement faible. Par exemple, la température
è max atteinte durant le régime quasi
permanent est de l'ordre de 0,017 (soit 57 °C) et 0,016
(soit 55 °C) pour Es/Es,ref = 0,4 et 2, respectivement. Aussi, il ressort
de l'analyse de cette figure que l'accroissement de l'épaisseur
adimensionnelle de la plaque conductrice Es, donc de son inertie
thermique, provoque un allongement de la durée de ce régime
quasi- stationnaire. Les valeurs respectives de cette durée pour
Es/Es,ref = 0,4 et 2, sont 0,022 (soit 996 s) et 0,032 (soit 1448 s). Ce
régime quasi- stationnaire s'achève lorsque la fraction liquide,
f, atteint des valeurs excédant 0,6. Lorsque la
température è max atteint la valeur critique, è
cr , la fraction liquide, f, atteint une
valeur d'autant plus proche de l'unité que
l'épaisseur adimensionnelle de la plaque est élevée.

0.035
1
0.9
0.03
0.12 0
0 0.02 0.04 0.06 0.08 0.1
X
Température limite adimensionnelle, cr
è
X
X
X
X
X
X
X
X
X
X
X X X
X
E /E
s
s,ref
0.4
X
X
X
0.6
1
X
1.6
X
2
X
0.025
èmax
0.02
0.015
0.01
0.005
0.8
0.7
0.6
f
0.5
0.4
0.3
0.2
0.1
Figure 3.24: Effet de l'épaisseur
adimensionnelle de la plaque conductrice sur les variations temporelles de la
température maximale adimensionnelle des sources de chaleur (traits
continus) et la fraction liquide (traits discontinus).
L'effet de l'épaisseur, Es, sur la
distribution de la température adimensionnelle dans la plaque
conductrice en X = - Es/2 est donné à la Figure 3.25,
à trois instants différents représentant les trois
régimes du processus de fusion. Comme il peut être observé,
au début du processus de fusion, les courbes relatives aux
différentes épaisseurs adimensionnelles présentent des
maximums situés à proximité de la source de chaleur
centrale. Ces maximums se déplacent près de la source de chaleur
supérieure pour les instants ultérieurs. A noter qu'au
début de la fusion du MCP, cette distribution de température est
pratiquement symétrique, à cause du transfert de chaleur
conductif qui prévaut durant cette période. Au cours du temps,
les mouvements convectifs s'établissent dans la cavité liquide
ainsi formée, et perturbent cette
symétrie. Lors du processus de fusion, la cavité
liquide s'élargit et la partie inférieure de la plaque
conductrice (0 < Y < 0,5) se refroidit
mieux comparativement à la partie restante de la plaque. Ce
refroidissement devient plus important avec la réduction de
l'épaisseur adimensionnelle, Es (voir Figure 3.25). Quant
à la partie restante de la plaque conductrice, l'impact de
l'accroissement de l'épaisseur adimensionnel, Es, se
répercute par une élévation de la température.
Aussi, on peut constater que l'augmentation de l'épaisseur
adimensionnelle, Es /Es,ref, entraîne une réduction de
la différence de température adimensionnelle au sein de la plaque
conductrice. Par exemple, à l'instant, ô = 0,051, cette
différence est égale à 0,0117 (14 °C) pour une
épaisseur adimensionnelle, Es/Es,ref = 0,4, tandis que pour une
épaisseur adimensionnelle, Es/Es,ref = 2, cette différence est
inférieure à 0,0066 (8 °C).
2
E s /Es,ref
0,4
1
2
ô=0,007
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035

ô=0,051
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
2
1.5
1
0.5
Y

ô=0,0844

0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
è
Figure 3.25: Profil de température
adimensionnelle au sein de la plaque conductrice pour
différentes épaisseurs adimensionnelles,
Es/Es,ref ( Es
X= - 2 ).
Le Tableau 3.9 donne la contribution au transfert de chaleur
des différentes surfaces de la paroi conductrice, exposées
à l'écoulement, pour différentes valeurs de
l'épaisseur adimensionnelle de la plaque conductrice, Es/Es,ref.
Tableau 3.9: Effet de l'épaisseur
adimensionnelle de la plaque conductrice sur le transfert de chaleur
échangé entre le MCP et les des différentes surfaces de la
plaque conductrice et des sources de chaleur à ô =
0,051.
Es /Es,ref Valeurs exprimées en % de la
puissance générée dans les sources de chaleur
0,4 14,00 19,00 7,70 21,00 7,20 18,50 7,00
0,6 16,05 18,60 7,60 19,87 7,00 17,80 7,70
1 18,74 18,63 7,24 19,85 6,78 17,30 8,50
1,6 20,60 18,10 7,10 18,30 6,40 15,90 8,70
2 22,40 18,10 6,90 17,70 6,00 15,40 8,73

S1 S2 S3
Plaque conductrice
L'analyse des données du Tableau 3.9 permet de
constater que l'accroissement de l'épaisseur adimensionnelle de la
plaque conductrice entraîne une augmentation des taux de transfert de
chaleur échangée par les parties inférieure et
supérieure de la plaque conductrice (de 14 % à 22,4 % pour la
partie inférieure et de 7 % à 8,73 % pour la partie
supérieure). Pour expliquer ce comportement, on peut faire appel, pour
le régime quasi permanent, à l'expression usuellement
utilisée pour l'approximation de la résistance de l'ailette
[21]:
1
R (3.5)
s (k h e l) 0.5
s c s
L'expression (3.5) montre que la résistance thermique
du substrat décroît avec l'accroissement de l'épaisseur du
substrat, es. Par conséquent, le transfert de
chaleur entre le MCP liquide et la paroi chaude s'intensifie. Le taux de
transfert de chaleur évacué par la
paroi chaude au MCP représente 94,2 % et 95,25 % de la
puissance générée par les sources de chaleur pour
Es/Es,ref = 0,4 et 2, respectivement. Ceci explique la chute de la
température maximale adimensionnelle durant le régime quasi
permanent (Figures 3.24 et 3.26).
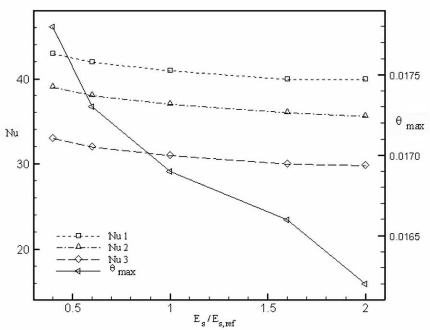
Figure 3.26: Effet de l'épaisseur
adimensionnelle, Es/Es,ref , sur la température
maximale
adimensionnelle, èmax , et le nombre de Nusselt
moyen des sources de chaleur, Nu, à ô =0,051
(régime quasi stationnaire).
La Figure 3.26 illustre l'effet de l'épaisseur
adimensionnelle, Es/Es,ref, sur le nombre de Nusselt moyen et la
température maximale adimensionnelle des sources de chaleur, durant la
régime quasi- permanent. L'effet de l'accroissement de
l'épaisseur adimensionnelle, Es est traduit par une
décroissance de la température maximale adimensionnelle (Figure
3.26) et des flux de chaleur adimensionnels évacués par les faces
des sources de chaleur (Tableau 3.9). L'expression (2.58) montre que le nombre
de Nusselt moyen de chaque source de chaleur est
Es augmente). Ainsi, la décroissance de J
?ç est légèrement compensée par
î ? î
O
K d
0
|
l'augmentation de
|
1
O , si bien que le nombre de Nusselt moyen de
chaque source de chaleur
max
|
subit une légère chute lorsque Es
s'accroît.
La Figure 3.27 donne l'effet de l'épaisseur
adimensionnelle, Es/Es,ref, sur la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide, f.
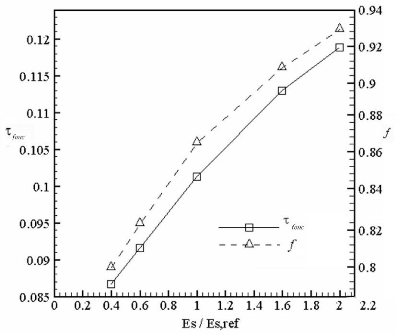
Figure 3.27: Effet de l'épaisseur
adimensionnelle, Es/Es,ref, sur la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide, f.
L'analyse des courbes de cette figure montre que la durée
ôfonc et la fraction liquide, f,
|
varient, approximativement, linéairement en fonction du
rapport
|
0.5
/ '
E s
~ ~
~ ~
Es,ref
|
dans la plage: 0,2 -
|
0,5
~~ ,
4. Les corrélations suivantes ont été
déduites:
~ E s
ô fonc = 0,059375 + 0,041925 ~ ~ E
s,ref
0,5
( ~
E s
f ,
= 0 70036 + 0,167647 (3.6)
~ ~
~ , )
E s ref
avec 0,4 < Es /Es,ref
< 2.
La comparaison des résultats numériques avec
ceux obtenus à partir des corrélations (3.6) est donnée
à la Figure 3.28, représentant la courbe de parité. Un
accord satisfaisant est obtenu. En effet, les variations maximales pour la
durée ôfonc et la fraction liquide, f, sont de
l'ordre
de 3 % et 1,5 %, respectivement.
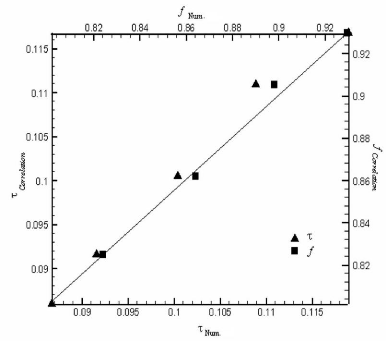
Figure 3.28: Courbe de parité
|
|



