3.4.4. Effet de la protubérance des sources de
chaleur, Ec

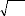
Il est important de rappeler que les simulations
numériques ont été conduites en utilisant les
données des Tableaux 3.1 et 3.2. Les volumes du MCP et des sources de
chaleur représentés
par leurs longueurs caractéristiques respectives, l o =
lw - 3l c e c et l CE = l c e c ,
sont
maintenus constants pour toutes les simulations numériques, (
lo = 0,06 m, lCE = 0,0067 m).
Dans cette section, l'effet de l'épaisseur
adimensionnelle des sources de chaleur, Ec, sur leur refroidissement
sera étudié. Puisque les dimensions de la cavité et la
quantité du MCP sont maintenues constantes, la hauteur adimensionnelle
de la source, Lc, doit être ajustée en utilisant la
relation: Lc = LCE / Ec où LCE = lCE/
lo, à chaque fois que l'épaisseur adimensionnelle,
Ec, varie. Plusieurs simulations numériques ont
été effectuées en considérant la plage de variation
de Ec/Ec,ref: 0,667 - 4.
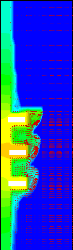
Un exemple illustrant le champ de température, la
structure de l'écoulement, la forme et la position du front de fusion
est donné à la Figure 3.19, pour deux instants adimensionnels,
ô1 =
0,0181 (soit 820 s) et ô2 =0,0733 (soit
3320 s). Comme on peut le constater, la forme et la
position du front de fusion, les isothermes et le champ des
vitesses sont fortement altérés par la protubérance des
sources de chaleur. Le profil des vitesses est parabolique dans la couche
limite qui se développe prés des parois solides. Pour les faibles
rapports Ec/Ec,ref, et dans son mouvement ascendant de convection
naturelle, le MCP liquide récupère la chaleur
évacuée par les trois sources de chaleur et la plaque
conductrice. Lorsque le MCP liquide atteint la paroi supérieure, il
subit une déflexion et descend le long du front de fusion en lui
transférant la chaleur avec une densité de flux de chaleur
décroissante dans la direction descendante. La nature
décroissante, dans le sens descendant, de la densité de flux de
chaleur, à l'interface solide- liquide, entraîne des taux de
fusion décroissant dans le même sens. Ceci explique la
déformation prononcée du front de fusion dans la partie
supérieure de la cavité. La présence

0.019
0.016
0.013
0.027
0.021
0.014
Ec/Ec,ref =0,667 1 2 4
(b)
(a)

0.02
0.018


0.021
0.022
0.020
0.017
.018
0.016

0.015
0.014
0.016
0.014
0.015
0.014
-
0.017
0.014

0.030 0.028 0.026 0.024 0.022 0.020 0.018 0.016 0.014 0.012
0.010 0.008 0.006 0.004 0.002 0.000

0.019 0.018 0.017 0.016 0.015 0.014 0.013 0.012 0.011 0.010
0.009 0.008 0.007 0.006 0.005 0.004 0.003 0.002 0.001 0.000

Figure 3.19: Effet de l'épaisseur
adimensionnelle des sources de chaleur, Ec/Ec,ref, sur les champs de
température, de vitesse, la position et la forme du front de fusion
(isotherme, è =0) aux instants adimensionnels (a):
ô1 = 0,0181 soit 820 s et (b):
ô2 = 0,0733 soit 3320 s
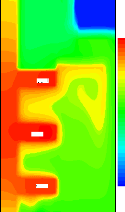
0.022
0.020
0.021
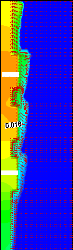
Figure 3.19.c: Structure en
plume au dessus de la
source
supérieure (ô =0,0733)
0.021 0.020 0.018 0.017 0.016 0.015 0.015 0.014 0.013 0.012
0.010 0.009 0.007 0.007 0.005 0.005 0.004 0.003 0.000
d'une cellule de convection prés de la source de
chaleur supérieure améliore le transfert de chaleur entre
celle-ci et le MCP liquide. Ce qui explique la température relativement
basse de la source supérieure et la déformation locale
marquée de l'interface solide-liquide. La chaleur
récupérée par le MCP liquide, lors de son mouvement
ascendant, est transférée au front de fusion qui avance plus
lentement dans la partie supérieure de la cavité en comparaison
avec sa progression dans la partie inférieure. Pour des rapports
Ec/Ec,ref élevés, la situation est localement
similaire à une cavité chauffée par le bas,
caractérisée par l'apparition de ` jets ` et une
structure en plume `panaches `. Cette structure altère
l'écoulement et donne naissance à un vortex anti-horaire au
dessus de la troisième source de chaleur (voir détail figure
ci-contre, Ec/Ec,ref = 4, ô = 0,0733). Ce vortex sépare
deux zones d'écoulement principales: zone inférieure et
supérieure. Dans la zone inférieure, le MCP liquide extrait la
chaleur des faces des sources de chaleur et de la plaque conductrice, pour
l'évacuer, en grande partie, au front de fusion, expliquant le
rapprochement rapide de celui-ci de la paroi droite. Dans la zone
supérieure, et dans son mouvement de convection naturelle, le MCP
liquide extrait la chaleur de la partie supérieure de la plaque
conductrice et de la face supérieure de la source de chaleur
supérieure et la transfère à l'interface solide- liquide.
Dans la partie inférieure de l'enceinte, la fusion est plus rapide en
comparaison à celle dans la partie supérieure. En effet, le
positionnement des sources de chaleur en bas de l'enceinte, où le MCP
liquide est relativement froid, contribue à l'amélioration du
transfert de chaleur et par conséquent à la fusion rapide du
MCP.
Une autre remarque qui se dégage de l'analyse de cette
figure est que la zone la plus chaude comporte les trois sources de chaleur et
une partie de la paroi conductrice. Il faut noter
que cette zone se déplace vers le bas de la
cavité lorsque l'épaisseur adimensionnelle, Ec,
augmente. Quant à la zone la plus froide, dépendamment de
l'épaisseur, Ec, elle peut être située soit en
bas soit en haut de la cavité. Cette zone renferme le MCP liquide ayant
déjà évacué sa chaleur au front de fusion lors de
son mouvement descendant. Il y a lieu de signaler que la Figure 3.19b
correspondant à l'instant ô2 = 0,0733 montre
l'état thermique et
hydrodynamique avancé du système (proche de la
fin du processus de fusion). On peut bien remarquer, que pour une
épaisseur adimensionnelle faible (Ec /Ec,ref
1), la fin du processus de fusion est marquée par la
présence d'un seul bloc de MCP solide dans la zone inférieure
droite de la cavité, alors que pour une épaisseur adimensionnelle
élevé (Ec /Ec,ref > 1) un bloc de MCP solide se
détache et se localise dans la zone supérieure du coté
droit de la cavité.
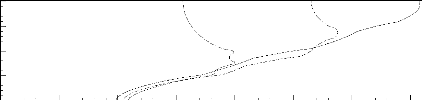
La Figure 3.20, donne le profil de température
adimensionnelle dans la plaque conductrice
en Es
X= - 2 , pour différentes valeurs de
l'épaisseur adimensionnelle, Ec/Ec,ref, à des
instants
adimensionnels représentant trois régimes du
processus de fusion. Cette figure montre que les faces latérales des
sources de chaleur, caractérisées par leur protubérance,
Ec, influencent fortement le transfert de chaleur. Les courbes de
cette figure sont ondulées au niveau des sources de chaleur. Les
maximums se situent directement près des sources de chaleur. Cette
figure montre aussi que, pour les faibles épaisseurs adimensionnelles
(Ec/Ec,ref = 0,667), le maximum est situé à
proximité de la source de chaleur supérieure, alors que pour les
épaisseurs adimensionnelles relativement élevées
(Ec/Ec,ref = 4), ce maximum est localisée près de la source
centrale. Il est à signaler que pour les faibles valeurs de
l'épaisseur adimensionnelle, Ec, la plaque est mal refroidie.
Ceci est dû à la structure de l'écoulement qui change avec
la variation de Ec, comme il a été décrit
précédemment. Il y a lieu de noter qu'à l'instant
ô = 0,095 la différence de température
adimensionnelle enregistrée dans la plaque, Äè s
, est de l'ordre de 0,026 (soit 31 °C) pour les faibles épaisseurs
adimensionnelles
(Ec/Ec,ref = 0,667); une valeur à comparer à 10,5
°C pour Ec/Ec,ref = 4.

E /E
c
ô= 0,018
4
0,667
1
c,ref
ô= 0,051
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
0

0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
ô= 0,095
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
è
Figure 3.20: Effet de l'épaisseur
adimensionnelle, Ec/Ec,ref, sur le profil de température
adimensionnelle au sein du substrat en Es
X= - 2 , à différents instants.
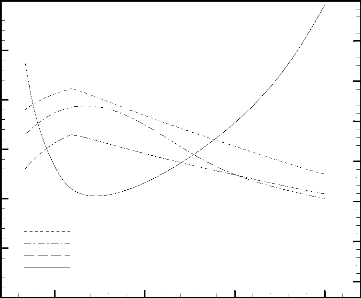
Les constatations précédentes sont
confirmées par l'analyse de la Figure 3.21 qui donne la variation du
nombre de Nuselt moyen, Nu, de chaque source de chaleur et la variation de la
température maximale adimensionnelle en fonction de Ec/Ec,ref
durant le régime quasi stationnaire. Lorsque l'épaisseur
adimensionnelle des sources augmente, le nombre de Nusselt moyen augmente et
atteint sa valeur maximale au voisinage de Ec/Ec,ref =1,2,
puis diminue avec l'accroissement de Ec. Pour Ec/Ec,ref
< 3, le nombre de Nusselt le plus faible correspond
à la source de chaleur supérieure, alors que pour
Ec/Ec,ref >3, c'est la source de chaleur centrale qui
présente le nombre de Nusselt moyen le plus faible. Ces
résultats reflètent fidèlement les
constatations observées précédemment
(Figure 3.19) concernant la localisation de la température maximale
adimensionnelle. Celle-ci est localisée sur la source de chaleur
supérieure pour Ec/Ec,ref < 1, alors que pour
Ec/Ec,ref > 1, cette température est enregistrée par la source
de chaleur centrale. La valeur de cette température augmente avec
l'accroissement du rapport Ec/Ec,ref. Ceci explique la
décroissance aiguée du nombre de Nusselt (qui est inversement
proportionnel à Omax , voir équation
(2.58) ). Lorsque Ec/Ec,ref = 3, la source
centrale présente le nombre de Nusselt le plus petit.
Nu 1
Nu 2
Nu 3
è max
1 2 3 4
E / E
c c,ref
Nu
30
40
20
60
50
10
0
0.021
0.02
0.019 0.018
è
max
0.017
0.016
0.015
0.014
Figure 3.21: Effet de l'épaisseur
adimensionnelle, Ec/Ec,ref, sur la température maximale
adimensionnelle, èmax , et le nombre de Nusselt moyen des
sources de chaleur, Nu, en régime quasi stationnaire, ô =
0,051.
Tableau 3.8: Effet de l'épaisseur
adimensionnelle des sources de chaleur sur le taux de transfert de chaleur
échangé entre le MCP et les des différentes surfaces de la
plaque conductrice et des sources de chaleur en régime quasi- permanent
(ô = 0,051).
|
Ec /Ec,ref
|
Valeurs exprimées en % de la puissance
générée dans les sources de chaleur
|
|
|
0,667
|
17,00
|
20,30
|
7,23
|
22,30
|
7,32
|
17,00
|
4,07
|
|
1
|
18,74
|
18,63
|
7,24
|
19,85
|
6,78
|
17,30
|
8,50
|
|
1,2
|
19,13
|
17,80
|
7,28
|
20,01
|
6,68
|
16,20
|
11,25
|
|
2,6
|
21,07
|
18,20
|
6,01
|
17,12
|
4,01
|
15,40
|
16,80
|
|
4
|
23,40
|
18,64
|
5,97
|
15,03
|
3,23
|
15,04
|
17,85
|
S1 S2 S3
Plaque conductrice
Le Tableau 3.8 donne la contribution au transfert de chaleur
des différentes faces de la paroi chaude, exposées à
l'écoulement, pour différentes épaisseurs adimensionnelles
Ec. L'analyse des données du Tableau 3.8 permet de confirmer
les constatations susmentionnées. Avec l'augmentation de Ec,
les surfaces de la plaque conductrice, situées dans les
microcavités, évacuent de moins en moins la chaleur en
comparaison avec les autres portions. Ceci est dû au faible mouvement du
MCP liquide capturé par les microcavités. La conduction thermique
prédomine au sein des microcavités, conduisant, ainsi, à
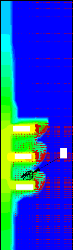
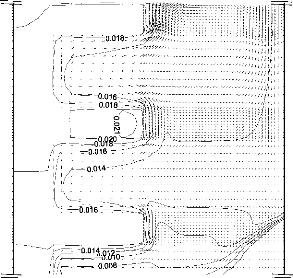
la surchauffe locale du liquide. La Figure 3.22 donne plus de détails
sur l'écoulement à l'intérieur des microcavités et
dévoile l'existence d'un faible mouvement comparativement à celui
trouvé dans la zone d'écoulement principale. Ce faible mouvement
est aussi à l'origine de la décroissance des taux de transfert de
chaleur transmis par les faces des sources de chaleur avec l'accroissement de
l'épaisseur Ec. L'accroissement de l'épaisseur
adimensionnelle, Ec, des sources de chaleur se traduit par le
déplacement descendant des centres des sources de chaleur et par
conséquent une augmentation de la surface d'échange de la partie
de la plaque conductrice située au dessus de la source
supérieure. Cet effet contribue à l'intensification du taux de
transfert de chaleur tel qu'illustré au Tableau 3.8.
S3
0.020
Plaque conductrice
S2
0.020
0.014
S1
0.018
0.016
Figure 3.22: Champ de vitesses au niveau des
microcavités pour Ec/Ec,ref =4, à l'instantô
= 0,051.
L'analyse du Tableau 3.8 montre que, pour la plage de
variation de Ec considérée, quelque soit
l'épaisseur adimensionnelle, Ec, pas moins de 35 % de la
puissance générée par les sources de chaleur est
transférée par les faces verticales arrières des sources
au MCP liquide. La contribution de la plaque conductrice, assurant la diffusion
de la chaleur, s'intensifie avec l'augmentation de l'épaisseur
adimensionnelle, Ec. Le Tableau 3.8 montre que lorsque le rapport
Ec/Ec,ref varie de 0,667 à 4, le taux de transfert de chaleur
évacué au MCP liquide correspond à 35,62 % et 50,45 % de
la puissance générée, respectivement. Quant aux faces des
sources de chaleur en contact avec le MCP liquide, leur contribution au
transfert de chaleur subit une décroissance en passant de 59,60 %
à 48,71 %, lorsque le rapport Ec/Ec,ref s'accroît de 0,667
à 4. De ce qui précède, il en résulte que le taux
de transfert de chaleur vers le MCP s'intensifie sous l'effet de l'augmentation
de l'épaisseur adimensionnelle en passant
d'une valeur de 95,22 % à 99,16 % de la puissance
générée par les sources.
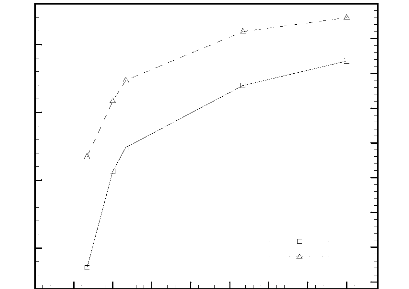
La Figure 3.23 présente l'effet du rapport
Ec/Ec,ref sur la durée adimensionnelle de fonctionnement
sécurisé, ôfonc , et la fraction liquide, f.
L'analyse de cette figure permet de
constater une nette amélioration de la durée
ôfonc avec l'augmentation du rapport Ec/Ec,ref.
Les
valeurs respectives de ôfonc , pour Ec/Ec,ref = 0,67 et 4
sont 0,0887 (~ 4013 s) et 0,117 (~
5294 s). En effet, comme il a été
susmentionné, l'accroissement de l'épaisseur Ec se
répercute sur le taux de transfert de chaleur en intensifiant celui-ci.
En conséquence, les sources de chaleur se refroidissent davantage et la
durée adimensionnelle de fonctionnement sécurisé
s'allonge. La fraction liquide, f, augmente, aussi, suite à
l'augmentation du taux de transfert de chaleur et de la durée de
fonctionnement sécurisé, ôfonc .
0 0.5 1 1.5 2 2.5 3 3.5 4
E c /E c,ref
0.85
f
0.8
1
ô
fonc
f
0.95
0.9
0.75
0.7
0.65
0.6
0.12
0.11
ô
fonc
0.1
0.09
Figure 3.23: Effet de l'épaisseur
adimensionnelle, Ec/Ec,ref, sur la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide, f.
En s'inspirant de la Figure 3.23, les corrélations
exprimant la durée adimensionnelle de fonctionnement
sécurisé, ôfonc , et la fraction liquide,
f, en fonction du rapport Ec/Ec,ref sont
-1,17 - 1 4
,
données par l'équation Eq.(3.4). La variation
maximale entre les résultats numériques et ceux donnés par
l'expression Eq.(3.4) est estimée à 2 %.
(3.4)
~
E ~ ~
E
c c
ô = 0 12243 0,02113
, - ~ ~ , 0 99107 0 12307
f ,
= - , ~ ~
fonc
~ )
E E
c ref
, ~ ~
c ref
,
avec 0,667 < Ec/Ec,ref <
4,0
|
|



