Memoire Online - Etude des transferts de chaleur dans une enceinte confinant un matériau à changement de phase et chauffée par des sources de chaleur protubérantes sur une paroi conductrice verticale

Dans cette section, l'effet de la diffusivité thermique adimensionnelle de la plaque conductrice sur le comportement thermique des sources de chaleur sera analysé. Les simulations numériques ont été effectuées en considérant la plage de variation du rapport des diffusivités thermiques á s / á s,ref : 0,02-2,38 avec á s,ref = 70,55, correspondant aux

valeurs fréquemment utilisées en électronique. La Figure 3.15 illustre l'effet du rapport
á s / á_s,ref sur l'évolution temporelle de la température maximale adimensionnelle des sources

de chaleur. Comme illustré sur cette figure, plus le rapport á s / á _s,ref augmente, plus la

montée de la température maximale adimensionnelle des sources de chaleur est lente
(pour á s / á _s,ref >1). En effet, l'accroissement de á s / á _s,ref augmente l'habilité de la plaque

conductrice à diffuser la chaleur en son sein, au lieu de la stocker sous forme sensible, et d'uniformiser sa température. La résistance thermique de la plaque conductrice diminue, favorisant, ainsi, la diffusion de la chaleur vers les parties inférieure et supérieure de la plaque conductrice. En conséquence, les températures moyennes adimensionnelles des sources de chaleur subissent une nette diminution.

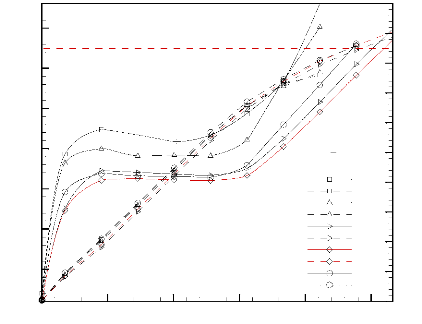
Figure 3.15: Effet de la diffusivité thermique adimensionnelle de la plaque conductrice, á s / á _s,ref, sur l'évolution temporelle de la température maximale adimensionnelle des sources

Il a été, aussi, constaté que la valeur optimale du rapport á s / á _s,ref correspondant à un meilleur

refroidissement des sources de chaleur, durant le régime quasi-stationnaire, est estimée à 1,75.
La température maximale adimensionnelle correspondant à ce régime est de l'ordre de 0,0160
(Tmax ~ 55,02°C). Pour des valeurs de á s / á s,ref > 1,75, la température adimensionnelle de la

plaque conductrice s'uniformise davantage (Figure 3.16), entraînant, ainsi, une diminution du gradient de température et du transfert de chaleur des sources de chaleur vers la plaque conductrice. Ceci se traduit par une légère augmentation de la température maximale adimensionnelle et du flux de chaleur adimensionnel à l'interface sources de chaleur- MCP liquide.

Ces résultats sont confirmés par l'analyse des Figures 3.16 et 3.17, illustrant le profil de température adimensionnelle de la plaque conductrice et la forme et la position du front de fusion pour différentes valeurs du rapport des diffusivités thermiques, á s / á _s,ref. L'analyse de

la Figure 3.16 montre que l'accroissement du rapport á s / á _s,ref réduit la température

maximale adimensionnelle et favorise l'isothermie de la plaque conductrice. Aussi, il est
important de signaler l'apparition de gradients thermiques élevés au sein de la plaque
conductrice, au niveau des jonctions des sources de chaleur, pour les faibles valeurs du

rapport á s / á _s,ref ( á s / á s,ref = 0,21). Ces gradients thermiques élevés risquent d'engendrer une déformation de la plaque conductrice (fissuration de la carte mère de l'ordinateur).

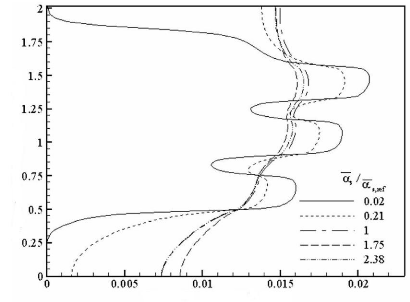
Figure 3.16: Effet de la diffusivité thermique adimensionnelle de la plaque conductrice

á s / á _s,ref sur le profil de température adimensionnelle au sein du substrat en Es

L'analyse de la Figure 3.17 montre que pour les faibles valeurs de á s / á _s,ref (~ 0,02), la plaque est similaire à une paroi non conductrice et transmet moins de chaleur. La chaleur est essentiellement évacuée par les faces des sources de chaleur. Au début de la fusion, des poches de MCP liquides prennent naissance autour de chaque source de chaleur. Les mouvements convectifs se manifestant dans cette zone sont insuffisants pour dissiper toute la puissance générée par les sources de chaleur. Ceci explique l'échauffement relativement rapide de ces dernières. Plus le rapport á s / á _s,ref s'accroît, plus la plaque conductrice contribue au transfert de la chaleur, en véhiculant celle-ci à partir des sources de chaleur vers le MCP. Le MCP liquide s'étale sur toute la surface chaude. Pour des valeurs de á s / á s,ref = 1 la courbure du front de fusion devient moins prononcée et indépendante du rapport á s / á _s,ref .

Il est à noter que la diffusion de la chaleur vers les parties inférieure et supérieure de la plaque conductrice entraîne un allongement de la cavité liquide et une diminution du volume des poches liquides entourant les sources de chaleur. Dans ce cas, la forme du front de fusion ressemble à celle obtenue pour le cas de la fusion par une paroi isotherme.

á /

^ás,ref

= 0,02 0,21 1 1,75 2,38

è max = 0,0209 (61°C)

0,0192 (59 °C)

0,0167(56 °C)

0,0151(54 °C)

0,0159(55 °C)

f = 0,207

0,203

0,180

0,190

0,210

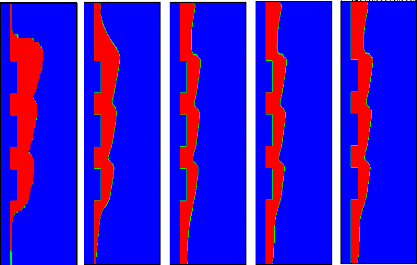
Figure 3.17: Effet du rapport des diffusivités thermiques, á s / á _s,ref , sur la forme et la position du front de fusion à ô = 0,018

La Figure 3.18 présente la variation de la durée adimensionnelle de fonctionnement sécurisé mise par les sources de chaleur pour atteindre la température adimensionnelle critique ( è max è _cr), pour différentes valeurs du rapport á s / á _s,ref. Il ressort de l'analyse de

cette figure que l'augmentation du rapport á s / á _s,ref a un effet appréciable sur la durée

adimensionnelle de fonctionnement sécurisé, ôfonc . En effet, lorsque le rapport á s / á _s,ref varie
de 0,02 à 1, la durée adimensionnelle de fonctionnement sécurisé s'accroît en passant de

ôfonc = 0 ,08 à ô fonc = 0 ,102. Mais à partir de á s / á _s,ref ~1, le taux de variation de ôfonc diminue lorsque á s / á _s,ref augmente. Pour des rapports plus élevés ( á s / á _s,ref> 1,75), la durée adimensionnelle de fonctionnement sécurisé, ôfonc , décroît. A cet effet, l'utilisation d'une plaque conductrice ayant un rapport á s / á _s,ref ~1,75 (substrat d'alumine, á _s ~123,28)

constitue un choix pratique correspondant à la valeur maximale de la durée adimensionnelle de fonctionnement sécurisé, ôfonc = 0 ,105_(tmax= 4752 s).

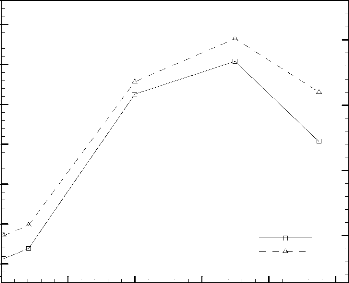
Figure 3.18: Durée adimensionnelle de fonctionnement sécurisé, _ôfonc , et fraction liquide, f, en fonction du rapport á s / á s,ref.

L'analyse de la Figure 3.18 montre, aussi, une augmentation du volume de MCP fondu avec la diffusivité thermique adimensionnelle de la plaque conductrice pour á s / á s,ref < 1,75.

La durée adimensionnelle de fonctionnement sécurisé et la fraction liquide ont été corrélées à partir des résultats numériques de la Figure 3.18. Elle sont données comme suit:

Le Tableau 3.7 montre un bon accord entre les résultats numériques et ceux obtenus par les corrélations (Eq.3.3). Les variations maximales pour ôfonc et f sont estimées à 2,42 % et

Tableau 3.7: Comparaison des résultats numériques (Figure 3.18) avec ceux obtenus par l'équation Eq.(3.3).

á_s

ôfonc

numérique

ôfonc Variation

corrélation ( %)

f
numérique

f
corrélation

Variation
(%)

ás,ref

Etude des transferts de chaleur dans une enceinte confinant un matériau à changement de phase et chauffée par des sources de chaleur protubérantes sur une paroi conductrice verticale

3.4.3 Effet du rapport des diffusivités thermiques, á s / á s,ref