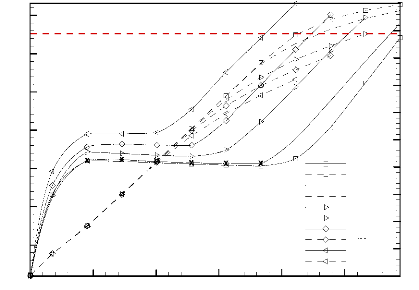
3.4.2 Effet de la distance adimensionnelle, Ä
La Figure 3.11 illustre l'effet de la distance adimensionnelle,
Ä, sur l'évolution temporelle de la température maximale
adimensionnelle des sources de chaleur, Omax , et
la fraction
liquide. Cette figure montre que le positionnement des sources
de chaleur en bas de la cavité
favorise un meilleur refroidissement
de celles-ci. Plus la distance adimensionnelle, Ä,
diminue, plus la
température maximale adimensionnelle, Omax ,
diminue et plus les durées du
régime quasi-stationnaire et de fonctionnement
sécurisé sont élevées. En effet, le
déplacement des sources de chaleur à la partie inférieure
de la cavité leur permet d'être en contact avec du MCP liquide
relativement froid, et par conséquent un échange de chaleur
important. Les températures maximales adimensionnelles atteintes par les
sources de chaleur en régime quasi stationnaire (à ô =
0,04), pour Ä /Ä ref = 1,667 et 0,667, sont respectivement
Omax = 0,0196
(Tmax= 59,44 °C) et Omax =
0,0157 (Tmax= 54,78 °C), soit une chute de température
de 5 °C.
Quant aux durées des régimes quasi-permanent, elle
sont respectivement 0,022 et 0,064, soit un accroissement de 0,042 ( ~1900 s =
31,67 minutes).
0.035
0.015
0.005
0.03
0.01
X
0
0 0.02 0.04 0.06 0.08 0.1
ô
Température limite adimensionnelle,
X
X
X
X
X
ècr
X
X
X
X
X
X
X
X
X
Ä /Ä
1.667
0.167
0.5
1
1.334
X
X
ref
X
X
0.9
0.8
0.7
0.2
0.1
1
0.025
è
max
0.02
0.6
f
0.5
0.4
0.3
Figure 3.11: Effet de la distance
adimensionnelle, Ä, sur la température adimensionnelle maximale
(traits continus) et la fraction liquide (traits discontinus)
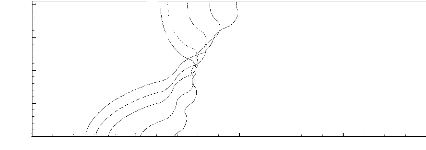
L'effet de la distance adimensionnelle, Ä, sur le profil
de température au sein de la plaque conductrice est
présenté à la Figure 3.12, pour deux instants
adimensionnels différents (ô = 0,04 et ô = 0,084). En
analysant les Figures 3.12a et 3.12b, il ressort que pour une distance
adimensionnelle donnée, Ä, la température adimensionnelle
augmente à cause du stockage d'énergie sensible dans la plaque
conductrice. L'accroissement de la température adimensionnelle est
d'autant plus élevé que la distance adimensionnelle, Ä, est
grande. Pour les faibles valeurs de Ä ( Ä /Ä ref 0,167) la
température adimensionnelle subit une légère
augmentation à cause du positionnement des sources de
chaleur en bas de la cavité. Ceci est dû à
l'intensification du transfert de chaleur entre le MCP liquide et les sources
de chaleur lorsque celles-ci sont positionnées en bas de la
cavité. Les profils de température présentés aux
Figures 3.12 a et 3.12 b présentent des maximums locaux localisés
prés des sources de
chaleur. Ces maximums se déplacent du coté droit
lorsque la distance adimensionnelle, Ä, s'accroît (sources se
déplaçant vers le haut de la cavité). L'intersection des
courbes de température résulte du rapprochement de la source de
chaleur supérieure de la paroi horizontale supérieure et de
l'éloignement de la source de chaleur inférieure de la paroi
horizontale inférieure, lorsque la distance adimensionnelle, Ä,
augmente. Le déplacement ascendant des sources de chaleur entraîne
un échauffement et un refroidissement de la plaque conductrice au niveau
des parties supérieure et inférieure, respectivement.
0,5
1
1,334
1
Y
1,667
(a)
0.5
0 0 0.01
0.02 0.03
è
2
1.5
ô =0.04 (1800 s )
A/A =0,167 ref

1
1,334
ô =0.084 (3800 s)
A/A =0,167 ref
0,5
(b)
1,667
0 0.01 0.02 0.03
è
Figure 3.12: Effet de la distance
adimensionnelle Ä / Ä ref sur le profil de
température au sein de la plaque conductrice ( E s
X= - ) aux instants adimensionnels, t = 0.04 et
0.084
2
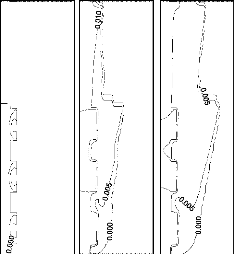
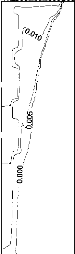
La Figure 3.13 donne l'évolution temporelle du champ
thermique au sein de la cavité pour deux valeurs de la distance
adimensionnelle: Ä / Ä ref = 0,167 et Ä / Ä ref
=1,667.
ô= 1.105 x 10 -4 0,029 0,051 0,0733 0,0844
0.001
0.001
0.001
MCP solide
0.016
0.015
0.016
MCP solide
0.015
0.015
0.015
MCP solide
MCP solide

MCP solide
0.010
0.015
0.015
MCP solide
0.015
0.016
0.005
0.015
MCP solide

MCP solide
(a)
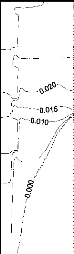
ô= 1.105 x 10 -4 0,029 0,051 0,0733 0,0844
0.001
0.001
0.020
0.015
0.015

0.020
0.015
0.020
0.015
0.020
0.025
0.030
0.025
0.005

0.030
0.020
0.005
0.030
(b)
Figure 3.13: Isothermes et position du
front de fusion (isotherme 0 =0): (a): Ä /Ä
ref =0,167,
(b): Ä /Ä ref =1,667.
L'analyse de cette figure montre que la position et la forme
du front de fusion et la structure des isothermes dépendent
étroitement de la position des sources de chaleur. En suivant le front
de fusion (isotherme 0 = 0) et en analysant sa forme les
remarques suivantes ont été dégagées:
· Pour le cas des sources de chaleur situées dans
la partie supérieure de la cavité ( Ä /Ä ref
=1,667), un bloc de MCP solide reste dans la partie inférieure de la
cavité.
Ce puits de chaleur refroidi inutilement la portion de la plaque
située en dessous de la source de chaleur inférieure (0 Y
Ä) ;
· Lorsque les sources de chaleur sont placées en bas
de la cavité ( Ä /Ä ref =0,167), un
bloc de MCP solide se détache et se localise devant la
source de chaleur située en haut de la cavité, à l'instant
ô = 0,0733. Ce bloc de MCP joue le rôle d'un puits de chaleur pour
la source de chaleur supérieure. C'est la raison pour laquelle les
sources de chaleur supérieure et centrale restent à l'abri de la
surchauffe ( è 1 et è 2 < è cr = 0,032),
pendant une durée relativement élevée;
· Les trois sources de chaleur sont bien refroidies
quand elles sont positionnées en bas de la cavité. Lorsque elles
sont déplacées vers le haut de la cavité, la source de
chaleur supérieure est rapidement surchauffée et sa
température adimensionnelle atteint la valeur critique. En effet,
après une durée adimensionnelle de fonctionnement ô
= 0,0844 (~ 3820 s) la température adimensionnelle de la source
de chaleur supérieure dépasse la valeur critique (
è 3 > è cr = 0,032), alors que les sources de chaleur centrale
et inférieure restent à l'abri d'une telle surchauffe.
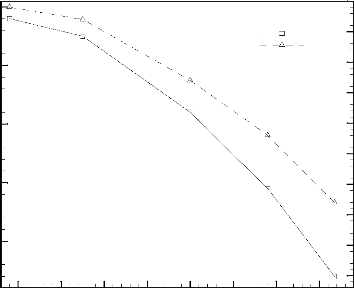
La Figure 3.14 donne la durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et la fraction
liquide correspondante, f, en fonction de la distance adimensionnelle,
Ä / Ä ref . L'analyse de cette figure montre que la
durée ôfonc et la fraction liquide, f, diminuent
avec l'augmentation du rapport Ä / Ä ref . Pour les
faibles valeurs du rapport Ä /Ä ref ( Ä /Ä ref
< 0,5),
tout le MCP solide est pratiquement fondu (f ~1)
à la fin du processus de fusion, tandis que
pour le cas où les
sources de chaleur sont placées dans la partie supérieure de la
cavité, plus
de 20 % du MCP reste à l'état solide (pour
Ä /Ä ref > 1,25), et le système atteint la
température
critique d'arrêt ( è max è cr ).
Ce cas n'est pas pratique pour le design des systèmes de refroidissement
de l'électronique (poids inutile).
ôfonc
f
0.12 0.11 0.1
ôfonc
0.09
0.08
1
0.95
0.9
0.85
0.8
f
0.75
0.7
0.65
0.6
0.55
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
Ä/Äref
Figure 3.14: Effet de la distance
adimensionnelle, Ä /Ä ref , sur la durée
adimensionnelle de fonctionnement sécurisé, ôfonc
, et la fraction liquide, f.
Les résultats de la Figure 3.14 peuvent être
traduits par des corrélations exprimant la durée adimensionnelle
de fonctionnement sécurisé, ôfonc , et la fraction
liquide, f, en fonction de la
distance adimensionnelle, Ä /Ä ref . Ces
corrélations sont données comme suit:
)1,6 1,8
Ä [ Ä )
ô fonc = 0,12134 - 0,02004 , f= 0,99937
- 0,13137 (3.2)
Ä ref Ä ref
avec 0,667 < Ä /Ä ref
< 1,667.
Le Tableau 3.6 montre un bon accord entre les résultats
numériques et ceux obtenus par les corrélations, Eq.(3.2). Les
variations maximales pourôfonc et f sont de
3,68 % et 0,87 %,
respectivement.
Tableau 3.6: Comparaison des résultats
numériques (Figure 3.14) avec ceux calculés par la
corrélation (Eq. 3.2).
|
Ä /Ä ref
|
ôfonc
numérique
|
ôfonc
corrélation
|
Variation
relative
(%)
|
f
numérique
|
f
corrélation
|
Variation
relative
( %)
|
|
0,167
|
0,115
|
0,11962
|
3,68
|
0,990
|
0,99743
|
0,75
|
|
0,50
|
0,115
|
0,11416
|
1,03
|
0,968
|
0,96500
|
0,31
|
|
1,00
|
0,101
|
0,10073
|
0,56
|
0,868
|
0,87136
|
0,39
|
|
1,334
|
0,089
|
0,08823
|
1,30
|
0,780
|
0,77605
|
0,51
|
|
1,667
|
0,074
|
0,07533
|
1,63
|
0,667
|
0,67278
|
0,87
|

|
|



